Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

1) Формулы с двойными номерами здесь – (7.2), (11.1) - и ниже – (7.5), (3.20), (9.5), (11.3), (11.5) – цитируются по книге [4].

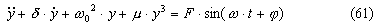2) Поскольку символ λ использован везде в настоящем разделе для обозначения корней характеристических уравнений.

где символом δ обозначена в соответствии с (7.5) удельная вязкость среды; ω₀, μ – (3.20), F – (9.5).

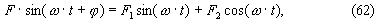Правую часть уравнения можно представить в виде суммы синусной и косинусной компоненты:

где F₁, F₂ определяются выражениями (11.3) и справедливы формулы (11.5).

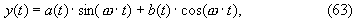При исследовании устойчивости для описания поведения рассматриваемой системы при появлении малых возмущений необходимо использовать полную подстановку Ван дер Поля:

       где a(t), b(t) – медленно изменяющиеся функции. Вычислим первую и вторую производные функции y(t) по времени t:

      

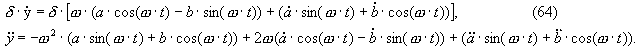
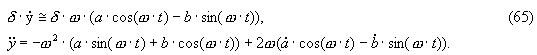       Используя медленность изменения функции a(t), b(t) и малость параметра δ, пренебрежем в формулах (64) слагаемыми вторых порядков малости:

Подставив последние выражения и (63) в уравнение (61), получим:

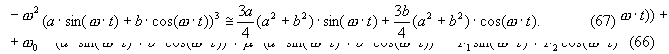
Тригонометрический двучлен третьей степени в левой части равенства без учета всех компонент, кроме колебаний с основной частотой ω может быть представлен в следующем виде:

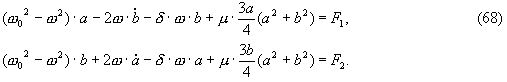Подставив это выражение в предыдущие и сгруппировав слагаемые с одинаковыми тригонометрическими функциями получим два соотношения:

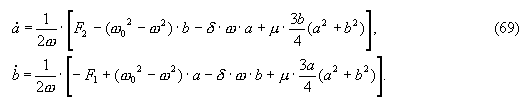Отсюда, разрешая равенства относительно a, b, можно записать систему «укороченных» уравнений:

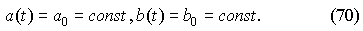Рассмотрим стационарное решение:

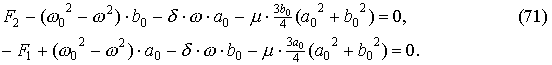Тогда для определения амплитуд стационарных колебаний a_0­­, b₀ на основании системы (69) получаем алгебраические уравнения:

 

Ранее решение (11.6) было получено в частном случае наличия одного только синусного колебания:

 

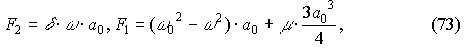       При этом из (71) получаем выражения:

 

совпадающие, как и следовало ожидать, с (11.9). Тогда. Использую (11.5), (73) можно записать формулу (11.10):

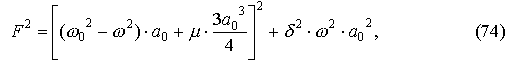
Определяющую резонансную зависимость рассматриваемого осциллятора | a₀ | ( ω ) или его «управляющую» характеристику | a₀ | (F).

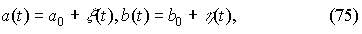Для исследования устойчивости полученных стационарных колебаний с амплитудами a₀, b₀ (70), (71) введем теперь в рассмотрение их малые возмущения ξ (t),η (t):

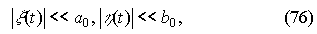где

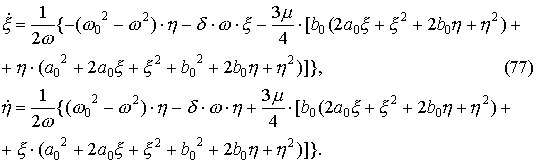Тогда подставляя (75) в укороченные уравнения (69) и используя условия для стационарных амплитуд (71), получим нелинейную систему возмущенного движения в следующем виде:

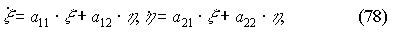Анализируем уравнения (77), используя малость возмущений (76):

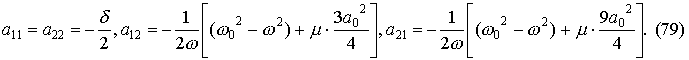где постоянные коэффициенты a_νm для частного случая, рассмотренного ранее (72), определяются так:

 

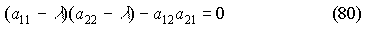Записывая возмущения в экспоненциальной форме (13), получая систему алгебраических уравнений (14), приравнивая нулю определитель этой системы (15), (16), окончательно получаем характеристическое уравнение в виде:

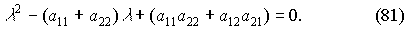или

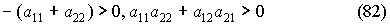Следовательно, необходимые и достаточные условия устойчивости линеаризованной системы можно записать так:

 

или, используя обозначения (79)

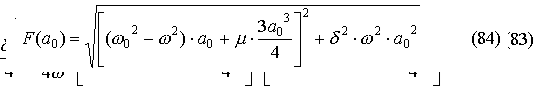Первое из этих условий в рамках рассматриваемой задачи, очевидно, выполняется всегда. Второе условие требует более детального анализа. Чтобы его осуществить, определим зависимость F(a₀) на основании соотношения (74):

 

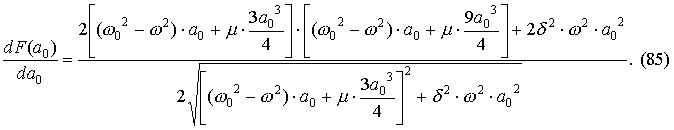
и вычислим производную dF/da₀:

Последнее выражение легко преобразовать к виду:

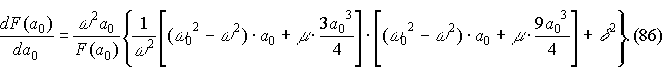
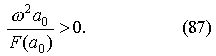Если теперь в этой зависимости амплитуду вынужденных колебаний a₀ (11.6) заменить на модуль этой величины |a₀|, как это обычно делается при построении резонансных характеристик | a₀ | ( ω ) осцилляторов и их управляющих характеристик | a₀ | (F), то никаких изменений в соотношении (86) не произойдет. В частности, знак производной не изменится. Таким образом, коэффициент при фигурной скобке в (86) является величиной существенно положительной.

Тогда, сравнивая выражение, заключенное в фигурные скобки в (86) с условием (83) видим, что условие устойчивости идентично условию положительности производной.

или условию положительности обратной величины

 

Следовательно, все точки управляющей характеристики осциллятора с положительным наклоном касательной соответствует устойчивым режимам колебаний. На рисунках?????????????? и 12.3 эти ветви изображены сплошными кривыми. «Падающей» ветви характеристики соответствуют неустойчивые колебания. На рис?????????? Эта ветвь представлена пунктиром, а на рис. 12.3 вообще отсутствует.

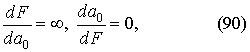В переходных точках перегиба кривой

имеет место упомянутый ранее «критический» случай, поскольку можно показать, что появляются корни характеристического уравнения с равными нулю вещественными частями. Анализа устойчивости на основе линейного приближения здесь оказывается недостаточно. Устойчивость или неустойчивость в этих точках определяют слагаемые высших порядков малости в уравнениях возмущенного движения.