В старой литературе по переменных звездам различают понятия "кривая блеска" (под которой традиционно понималась таблица, например, приведенного выше вида) и "график кривой блеска" (графическое представление этой таблицы). Такая терминология не соответствует общепринятому в науке словоупотреблению и нами применяться не будет.

Кривая блеска непериодической переменной звезды - это график зависимости звездной величины от времени. Если же изменения блеска имеют периодический характер, наглядность кривой блеска может быть значительно повышена, если привести наблюдения к одному периоду. Пусть элементы изменения блеска переменной звезды имеют вид:

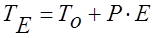                                                                                 (2.10)

Здесь T₀ - начальная юлианская дата максимума (минимума) блеска

      Р₀ - период (в сутках);

      Е  - текущий номер эпохи максимума (минимума) блеска, отсчитываемый от момента  T₀.

Для любого момента времени T > T₀ можно ввести величину Ф, которая называется фазой и выражается следующей формулой:

                               Ф = Fract {(T - T₀) / P},             (2.11)

где символом Fract обозначена дробная часть числа.

Известно, что период изменения блеска Алголя равен 2,86732 суток. Как можно определить его с такой точностью? Для этого сравнивают между собой достаточно удалённые по времени моменты минимума блеска. Каждое определение минимума редко бывает точнее 1-2минут, т.е. около 0,001 суток. Но, если разделить разность моментов минимумов на количество протекших между ними периодов, то точность определения среднего значения периода значительно повышается.

Формула (2.10) используется как для представления уже наблюдавшихся минимумов блеска затменно-переменных, так и для вычисления моментов будущих минимумов блеска. Вычисленные по ней моменты минимумов обозначают буквой С (от английского слова Calculated – вычислено), а наблюденные моменты – буквой О (от английского слова Observed –наблюдалось). Их разность обозначают О-С.

Сопоставление значений О-С с номерами Е даёт возможность судить о постоянстве или переменности периода. Для этого строится график О-С. Если период остаётся постоянным, то все точки расположатся около горизонтальной оси, с небольшими случайными отклонениями.

Если же график O-C представляет собой кривую линию, имеют место изменения периода. Здесь интересны следующие частные случаи. Если кривая - квадратичная парабола, то период - линейная функция времени. Рассеяние точек около синусоиды говорит о гармоническом законе изменения периода. Нередко график O-C удовлетворительно представляется ломаной линией. Это говорит о наличии интервалов времени, в течение которых период постоянен, меняясь между ними практически скачкообразно.

Причины изменений периодов весьма разнообразны. Например, переменная звезда b Лиры увеличивает свой период из-за непрерывной потери вещества. Наблюдался случай внезапного увеличения периода W Большой Медведицы после вспышки её блеска, вызванной, извержением огромного протуберанца.

Другой причиной изменения периода является наличие третьей звезды в системе. Обычно третья звезда находится на большом расстоянии от затменной пары. Например система Алголя имеет третью компоненту, которая удалена от затменной пары так, что период её орбитального движения составляет 1,873 года.

В случае переменных звезд, быстро меняющих свой блеск, принято приводить моменты наблюдений к центру Солнца (чтобы избежать влияния на характерные точки кривой блеска периодического движения Земли по орбите, которое, в частности, может создавать иллюзию изменений периода). Для этого используют формулу:

где Dt - поправка к моментам наблюдений, l и b - эклиптические координаты звезды, L_¤  - долгота Солнца в момент наблюдений. В более редких случаях особо быстрой переменности имеет смысл учитывать поправку, приводящую наблюдения не к центру Солнца, а к барицентру Солнечной системы. Эта поправка не превышает 16,6мин. и при наблюдении долгопериодических переменных ей можно пренебречь.

Глава 3.