Введение данного понятия необходимо по нескольким причинам: первая причина заключается в том, что для построения такой педагогической модели, которую мы используем в данной работе, необходим какой-то определенный идеализированный подход к олимпиадным заданиям. То есть нужно представить себе идеальный случай, при помощи которого можно описать (математически и, главное, педагогически) все реально встречающиеся варианты. Вторая причина состоит в том, что для построения шкалы сложности задач, нужно иметь какой-то базовый элемент, относительно которого и происходит построение этой шкалы.

В данном параграфе описывается лишь формальное введение основного понятия данной теории. В полном описании математического вывода и доказательства педагогической оправданности сбалансированного комплекта задач нет необходимости в силу того, что сама по себе автоматизированная система не использует этого понятия, а использует только математические выводы, которые сделаны на его основе.

 Под сбалансированным комплектом олимпиадных заданий, в контексте данной работы, будем понимать такой комплект заданий, в котором максимально равномерно воссоединены жесткий, естественный и щадящий режимы испытания для вывода серии всех испытаний школьников на гуманное отношение к личности школьников и бережное отношение к их талантам. В рамках представлений обсуждаемой модели, исходят из двух видов учебной деятельности учащихся и объясняют разный уровень сложности задач разным насыщением их решений формальными и творческими моментами. Эти требования к комплекту тождественны требованиям сбалансированности и полноты этого комплекта по отношению к репродуктивному, продуктивно-репродуктивному и продуктивному видам деятельности учащихся.

Хочется обратить внимание на то, что сбалансированный комплект представляет собой лишь идеализированную модель педагогического испытания школьников на олимпиадах. Ясно, что такой комплект в реальных условиях подобрать крайне сложно, однако он позволяет судить о том, какими должны быть олимпиадные задания, чтобы, в результате, можно было максимально приблизится к идеалу.

Вопрос об уровне сложности задач носит в рамках рассматриваемой теории достаточно важный характер. Наиболее исчерпывающий ответ на него может дать шкала сложности задач. Основные особенности подобной шкалы непосредственно оговариваются в исходных положениях теории. В связи с этим, следует упомянуть два момента. Первый момент заключается в том, что для полного анализа задач достаточен учет двух различных и несводимых друг к другу видов учебно-познавательной деятельности школьника – репродуктивной и продуктивной. Второй момент изначально оговаривает большие способности каждого школьника к репродуктивному виду деятельности по сравнению с продуктивным. Этот момент условно выразим неравенством: .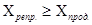

Принципиальная особенность указанных моментов заключается в том, что они определяют заведомо двумерный характер шкалы сложности задач. На этой шкале каждая задача должна характеризоваться двумя индексами, учитывающими два вида деятельности учащихся. В соответствии с этим любой единый показатель уровня сложности задач должен быть двумерным объектом. Это касается всех возможных шкал, включая и простейший случай ранжированной шкалы, оперирующей лишь целочисленной нумерацией уровней сложности задач. Она должна быть также двойной. Из всего сказанного выше ясно, что каждая задача в комплекте характеризуется точкой с координатами (k _n, k _p) на шкале. Где k _n – индекс задачи, характеризующий продуктивный (творческие задачи) вид деятельности, а k _p – индекс, характеризующий репродуктивный (типовые задачи) вид деятельности.

Кроме всего прочего, для построения шкалы сложности особую значимость имеет местоположение на ней двух задач – «очевидной» и «недоступной», ограничивающих весь возможный диапозон сложности задач. «Очевидную» задачу можно определить как задачу, которую полностью решают все участники без исключения. В решении «недоступной» задачи ни один из участников не способен сделать даже одного оцениваемого шага.

Возможен еще один интересный вариант задачи. Такую задачу условно назовем «нулевой». Она соответствует равновероятному распределению участников по набираемым баллам. «Нулевую» задачу можно одновременно считать как творческой, так и типовой.

Сама шкала сложности, согласно теории, имеет вид, представленный на рис. 1:

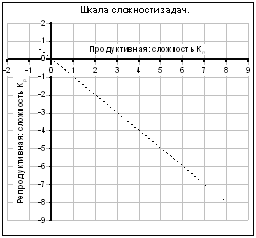
Рис. 1. Вид шкалы сложности.

Крайне интересным представляется расположение на этой шкале «очевидной», «недоступной» и «нулевой» задач. Очевидно, исходя из определения задач, видно, что «очевидная» задача – это есть предельный случай самой простой типовой задачи, то есть располагается она на оси ординат в −∞. «Недоступная» задача – есть предельный самый сложный случай творческих задач, располагается на оси абсцисс в +∞. «Нулевая» же задача, в силу своей двойственности, располагается на шкале в единственно пригодном месте – точке (0,0). Данная шкала недаром называется шкалой сложности, ведь видно, что усложнение творческих задач выражается перемещением точек, соответствующих задачам, вправо, вдоль оси абсцисс, а усложнение типовых задач – вверх, вдоль оси ординат.

Возникает вопрос: как же отображается на шкале сбалансированный комплект задач? Ответ вполне очевиден – сбалансированный комплект отображается направленными отрезками прямых, проходящих перпендикулярно к биссектрисе главного координатного угла (см. рис. 1), и, как следствие, пересекающих координатные оси под углом в 45°. При этом направление этих отрезков указывает увеличение сложности от задачи к задаче во всем комплекте. Если привести простой пример с комплектом из 2-х задач, то получим следующую шкалу:

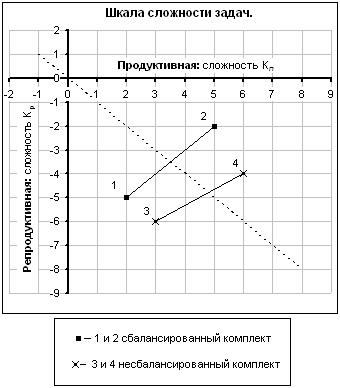
Рис. 2. Шкала сложности для двух комплектов из 2-х задач.

Для данного примера: комплект задач 1 и 2 считаем сбалансированным (задача 2 сложнее задачи 1), а комплект 3 и 4 считаем несбалансированным (задача 4 сложнее задачи 3).

Данная шкала имеет огромное практическое значение, так как позволяет с большой точностью определить, является ли данный комплект задач сбалансированным или нет. Поэтому она используется в разработанной программе в качестве одного из показателей качества задач.

§5. Требования к олимпиадным заданиям. Основные показатели качества.

Введенное в §4 понятие сбалансированного комплекта олимпиадных заданий является краеугольным, и на его основе строятся основные требования к составителям этих заданий. Из данного понятия следуют следующие требования:

1. Все задания, которые предлагаются участникам олимпиады, должны быть разноуровневыми. Это необходимое условие для проведения олимпиад. При полной реализации этого требования осуществляется первый шаг к возможности дифференцированного подхода. Задачи должны быть разной сложности. При этом необязательно различие максимального балла за сложные и простые задачи. На мой взгляд, это является отпугивающим фактором для слабых учеников (эта задача сложная, я ее все равно не решу, а поэтому решать не буду) и заманивающим для сильных (за эту задачу дают большой балл, поэтому лучше решить две задачи по 10 баллов, чем четыре по 5). Учащиеся заранее видят сложность (или простоту) задачи, что крайне нежелательно. Если же все задачи имеют одинаковую балльную стоимость, то есть вариант, что потенциально слабый участник додумается до сложной задачи, а это поднимет его самооценку. В этом выражается гуманистический подход к олимпиаде.

2. Второе требование к олимпиадным заданиям – они должны быть максимально приближены к идеальному сбалансированному комплекту, то есть должны в равной степени затрагивать продуктивную и репродуктивную деятельность школьников. Это выражается симметрией точек на шкале сложности (см. выше) относительно биссектрисы главного координатного угла. На распределении по суммарному баллу (S, ή₁) приближение к сбалансированному комплекту выражается в колоколообразном виде этого распределения.

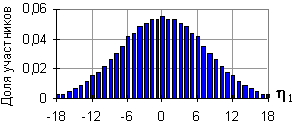
Рис. 1. Идеальный вид распределения по ή_1.

3. Третье требование заключается в том, что после проверки заданий и распределения участников по местам должно иметь место однозначное расположение участников на местах. То есть не должно быть несколько мест одного «достоинства». Если это требование выполнено, то можно говорить о максимальной реализации дифференцированного подхода и сбалансированного комплекта заданий.

Кроме вышеописанных требований, можно выделить еще достаточно много других, но мы ограничимся тем, что есть. Эти три требования в математическом виде реализованы в разработанной системе в виде трех параметров качества заданий.

Очевидно, что заранее невозможно предугадать о том, как будет разворачиваться обстановка при решении тех или иных заданий. В итоге, мы оперируем с протоколом результатов олимпиады и поэтому не можем точно направить ее ход в нужное русло. Однако, при помощи системы, можно оценить прошедшую олимпиаду и сделать выводы относительно следующей. В этом нам помогают три парамера качества заданий, которые полностью базируются на 3-х основных требованиях. Параметры эти таковы.

1) Процент реализации сложности задач. Этот параметр представляет собой математической выражение первого требования. Выражается он в процентах (%). В идеале должен быть, очевидно, равен 100%. Реально, такое значение получить крайне сложно, поэтому нормальным результатом можно считать 80-95%. Параметр зависит от количества блоков (для разного количества блоков – разный расчет). Если блок один, то параметр равен нулю и смысла, с точки зрения теории не имеет. Рассчитывается он следующим образом. В контексте данной теории этот параметр может быть использован применительно к каким-либо двум блокам заданий, то есть позволяет оценить, удалось ли реализовать большую сложность для одного блока задач относительно другого. Отсюда исходит принцип разного расчета для разного количества блоков. Практически, смысл расчета этого показателя сводится к следующему. При составлении олимпиадных заданий мы заранее знаем о том, какой блок является более сложным с точки зрения его решения, а какой – более легким. После решения этих блоков участниками, у нас есть реальные результаты для каждого блока. Далее, берется общий балл для более сложного блока (x₁) и общий балл для более легкого блока (x₂) (для каждого участника) и подсчитывается их разница (x₁-x₂). После проведения данных расчетов, строится гистограмма, подобная той, что изображена на рис. 2.

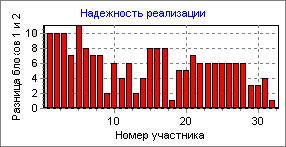
Рис. 2. Надежность реализации неравенства x₁≥x₂.

После построения такой гистограммы необходимо подсчитать число участников, для которых эта разница оказалась положительной (для данной гистограммы: общее количество участников равно 32, и разница x₁-x₂ положительна для всех, то есть надежность реализации – 100%). Далее, берется процент этого количества от общего количества участников.

2) Сбалансированность комплекта. Этот параметр представляет собой второе требование, выраженное в графической форме. В идеале, точки на графике должны быть максимально симметричны относительно биссектрисы угла (об этом читайте в §4). Расчет этого параметра требует дополнительных введений и кардинально отличается для комплектов с разным количеством блоков. Стоит заметить, что в случае, если все задания помещены в один блок, параметр не имеет смысла.

3) Коэффициент распределения по местам. Данный параметр представляет собой, очевидно, третье требование. Диапазон значений параметра [0..1]. В идеальном случае должен быть равен 1 (каждый участник находится на своем заслуженном месте), в самом худшем случае равен 0 (все участники заняли 1 место). Расчет этой величины прост: 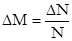, где ∆N - количество мест, N – общее количество участников.

Таким образом, рассчитав и визуализировав эти три параметра, можно с большой точностью сказать о реализации приведенных выше требований, а исходя из требований – сделать вывод об олимпиаде в целом.

Этими двумя задачами (распределение мест и оценка качества) занимается специальная программа, которая будет полностью описана в следующей главе.