Современные численные методы решения задачи нестационарной теплопроводности разделены на три математических метода: метод конечных разностей; метод конечных элементов; метод граничных элементов. Все три метода широко используются, каждый из них наделен своими достоинствами и недостатками. В нашем случае выбран метод конечных разностей. При построении разностных алгоритмов для численного решения дифференциальных задач важно, чтобы построенная конечно-разностная схема правильно отражала основные особенности физического процесса, описываемого исходными дифференциальными уравнениями. В частности, всегда надо стремиться к тому, чтобы разностный алгоритм выражал на сетке основные законы сохранения (тепла, массы, энергии и т.п.), положенные в основу исходной дифференциальной задачи. Большинство задач теплопроводности являются нелинейными, большое влияние на процессы распространения тепла оказывает температурная зависимость коэффициентов теплоемкости и теплопроводности материалов в высокотемпературных процессах, а также их изменение при межфазных превращениях. Учет этой зависимости приводит к нелинейным уравнениям теплопроводности. Нелинейными уравнениями описываются и процессы распространения тепла в телах, имеющих нелинейные источники, а также в случае наличия на границе нелинейных условий теплообмена.

В результате формирования входной геометрической информации мы получили двумерный массив размерностью 500 на 500 элементов, каждый элемент которого принадлежит телу отливки или формы и имеет индексное обозначение [I,j], где I,j=1…500. При переходе к конечным разностям распределение температуры в металле и форме имеет ступенчатый вид. Зафиксируем координаты точек с шагом dx, при этом x=i·dx, где i=0,1,2,3… , max(i) будет определять количество точек по горизонтали и соответственно геометрические размеры. То же самое необходимо произвести по второй координате y, y=j·dy, где j=0,1,2,3… , max(j) и таким образом мы зададим информацию о геометрии той части отливки, которую необходимо исследовать. Толщина у всех отдельных элементов конечно-разностной сетки одинаковая и равняется dz.

В работе[9] предлагается методика по расчету продолжительности заполнения металлом формы и расчета локальных зон прогрева формы при ее заполнении. Данная методика используется в качестве предварительного расчета и подробно здесь не описывается. При расчете затвердевания крупных стальных отливок сложной конфигурации такой расчет необходим, т.к. время заполнения формы металлом достаточно большое и продолжительность контакта металла с формой будет отличаться для различных частей отливки.

Для условия мгновенного заполнения металлом формы элементам массива входной информации присваиваются значения температуры заливки металла или начальной температуры формы.

Для описания теплообмена в системе отливка – форма для плоской стенки необходимо решить задачу о распределении температуры в металле и форме. Фундаментом решения задачи является численная аппроксимация уравнения Фурье.

Подход, используемый в методе конечных разностей, получил дальнейшее развитие в виде его модификаций – методе элементарных балансов.

 Метод элементарных балансов был впервые предложен в 1946 году советским ученым А.П.Ваничевым. Отличительной особенностью метода элементарных балансов является возможность решения задачи нестационарной теплопроводности для составных тел и для сред с переменными теплофизическими свойствами.

Метод элементарных балансов предполагает, что теплоемкость каждого n-го элемента сосредоточена в центре самого элемента (рис.14.4), каждый элемент соединен с соседним элементом тепловыми связями, по которым происходит передача тепла.

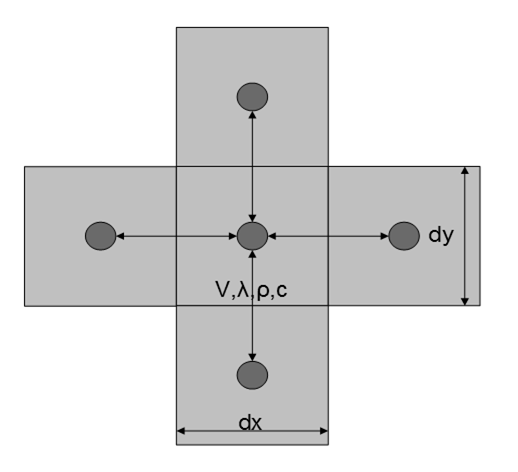
Рис.12.5. Геометрическая интерпретация метода элементарных балансов

При дискретизации геометрической модели отливки конечно-разностной сеткой I-уровня каждый элемент обладает рядом параметров, таких как объем, плотность, теплоемкость, теплопроводность, количество граней элемента, расстояние между центрами тяжести соседних элементов. При дискретизации первого уровня элементы могут иметь различный размер и форму, что определяется различными требованиями к точности расчета.

В основу метода принимаем следующие условия:

- увеличение энтальпии элементарного объема, принадлежащего данному узлу, пропорционально приращению температуры в этом узле;

- изменение температуры между расчетными точками (узлами) происходит по линейному закону и определяется термическим сопротивлением тепловых связей;

- изменение температуры во времени происходит дискретными скачками.

Если в сечении выделить слой Δx, а все расчеты вести для пластины единичной площади, то тогда элементарный объем слоя можно выразить

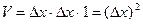                               .                                (12.1)

Теплота, переданная по слою x, по связи элементов с индексами I, (i+1) на основании принятых условий может быть выражена

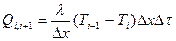                             ,                            (12.2)

а теплота, переданная по связи элементов с индексами I, (i-1),

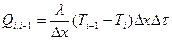                            .                              (12.3)

Здесь принимается, что T_i-1,T_i,T_i+1 – температуры узлов, рассчитанные в один и тот же момент времени. За время Δτ температура элемента с индексом I изменится, поскольку к нему подведена теплота Q_i,i-1, Q_i,i+1; это изменение можно определить из соотношения

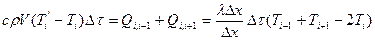           ,           (12.4)

где 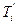- температура элемента I, рассчитанная к концу интервала времени Δτ(температура элемента изменяется скачками).

Соотношение (12.4) является уравнением теплового баланса, из него следует, что

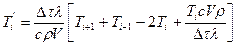                              _.                                                 (12.5)

Если учесть, что 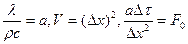, то тогда формула (12.5) примет следующий вид:

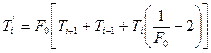                         .                              (12.6)

При выборе временного интервала Δτ, удовлетворяющего условию F₀=0.5, получим

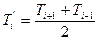                                   .                                          (12.7)

Как видно, уравнение (12.7) имеет тот же смысл, что и в случае решения задачи при помощи метода конечных разностей. Условие F₀=0.5 не является обязательным, возможно задавать любые значения числа Фурье меньше 0.5. Чем меньше число Фурье, тем точнее решение, но одновременно с точностью увеличивается трудоемкость вычислений, а применительно к компьютерному варианту вычислений – время счета. Для трехмерных задач рассматривают пространственные связи элементов.

Для компьютерной реализации расчета остывания отливки в форме разработана специальная методика расчета. В конечно-разностном расчете применяется метод элементарных балансов, в котором уравнение теплового баланса для i-го элемента разбиения сетки имеет следующий вид:

       å ^m _j=1 kⁿ  _{i, j} (T_iⁿ – T_jⁿ)F _i,j D t = c_i G_i (T_iⁿ – T_jⁿ) ,             (12.8)

где k – коэффициент теплопередачи между элементами i и j ;

m – количество неадиабатных граней элемента;

F – площадь контакта между элементами i и j;

c и G – удельная теплоемкость материала элемента и его масса;

Dt - временной шаг; n – временной индекс.

На контакте элемента i с элементом j коэффициент теплопередачи определяется по формуле: k_{i , j} = 1/(L_i/l_i + L_j /l_j), где L – расстояние от центра тяжести “i”- элемента (с коэффициентом теплопроводности l) до соседнего элемента по направлению движения теплового потока.

Метод элементарных балансов рассматривает элементы конечно-разностной схемы, как элементы с различными теплофизическими свойствами (теплоемкость, плотность, теплопроводность и т.д.), но закон теплопередачи не изменяется для всех элементарных объемов независимо от того принадлежат они металлу или форме.

Для вычисления двумерного распределения температуры организуются две аналогичные описанной подпрограммы, одна из которых рассчитывает значения температуры по строчкам, другая – по столбцам, при одном и том же шаге по времени.

На рис.12.5 приведены результаты расчета остывания сечения отливки типа корпус нагнетателя для различных моментов времени (50-1000с).

Рис.12.6. Расчет остывания металла в сечении отливки

корпус нагнетателя для различных моментов времени

На каждом шаге по времени имеем расчетное поле температур, которое можно анализировать на предмет достижения в любом элементе температуры солидус. При этом фиксируется текущее время, при котором достигнута температура солидус в данном элементе. Таким образом, формируется массив времени затвердевания для рассматриваемого сечения отливки. Контролируя, таким образом, все узлы к моменту затвердевания всего сечения отливки, сформируется двумерный массив продолжительности затвердевания узлов отливки (рис.12.7). Обработка массива продолжительности затвердевания далее осуществляется с целью расчета в каждом узле относительного временного градиента затвердевания

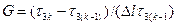 (12.8.)

где

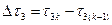- разница времени затвердевания питающего и питаемого объемов;

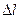- расстояние между этими объемами;

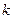- номер слоя, в котором находится малый объем.

Расчеты выполняются раздельно в вертикальном и горизонтальном направлении, затем производится их геометрическое суммирование.

В результате сформировалось поле затвердевания расчетного сечения отливки. Величина градиента полностью отражает степень питания данного узла (точки) отливки, т.е. распределение градиента является аналогом распределения свойств металла в расчетном сечении.

Рис.12.7. Эпюра продолжительности затвердевания

элементов участка отливки корпус нагнетателя

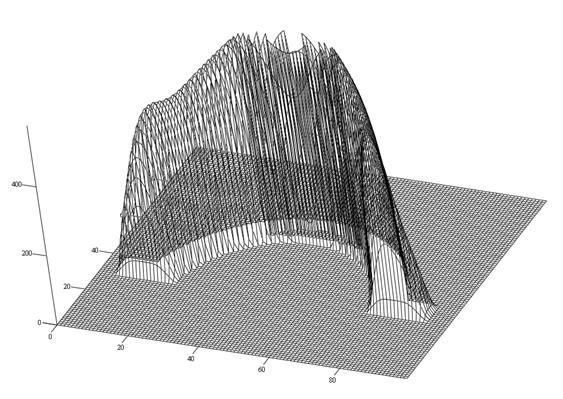
Рис.12.8. Эпюра продолжительности затвердевания

элементов участка отливки корпус цилиндра паровой турбины