В зависимости от взаиморастворимости компонентов различа­ют следующие типы бинарных смесей:

1) смеси взаиморастворимых жидкостей, т. е. таких жидкостей, которые растворимы друг в друге в любых соотношениях;

2) смеси жидкостей, нерастворимых друг в друге;

3) смеси частично растворимых жидкостей.

На рис. 1 представлены равновесные кривые для идеальной смеси (линия 1) и для реальных смесей с разными отклонениями от закона Рауля (кривые 2... 4).

Для реальных смесей равновесная кривая может быть рассчи­тана только по известным коэффициентам активности, определе­ние которых затруднено. Поэтому диаграмму y - x обычно строят на основе опытных данных.

Для ряда смесей количественные отклонения от закона Рауля настолько велики, что приводят к качественному изменению свойств смесей.

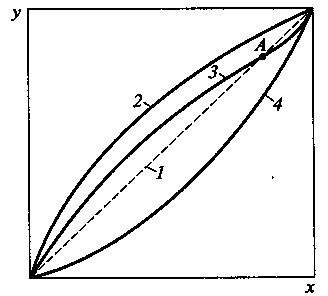
Рис. 1. Диаграмма равновесия у-х:

1 — для идеальной смеси; 2 —- смесь с положительным отклонением; 3 — азеотропная смесь; 4 — смесь с отрица­тельным отклонением

При определенном составе такие смеси имеют постоянную тем­пературу кипения, и концентрации пара и жидкости равны (у = х). Такие смеси называются азеотропными, или нераздельно кипя­щими (см. рис. 10.2, кривая 3). Точка А, в которой кривая составов фаз пересекает диагональ на диаграмме у—х, называется азеотропной точкой. Она указывает состав смеси, которая при данном давлении не может быть разделена на составляющие ее компоненты. Разделить ее можно путем изменения давления при перегонке. При изменении давления азеотропная точка перемещается на равновесной кривой.

Лекция №9

Холодильные процессы.

Холодильные установки

Второй закон термодинамики

Второй закон термодинамики (как и первый — закон сохранения энергии) установлен эмпирическим путем. Впервые его сформулировал Клаузиус: "теплота сама собой переходит лишь от тела с большей температурой к телу с меньшей температурой и не может самопроизвольно переходить в обратном направлении".

Другая формулировка: все самопроизвольные процессы в природе идут с увеличением энтропии. (Энтропия — мера хаотичности, неупорядоченности системы).

Рассмотрим систему из двух контактирующих тел с разными температурами. Тепло пойдет от тела с большей температурой к телу с меньшей до тех пор, пока температуры обоих тел не выровняются. При этом от одного тела к другому будет передано определенное количество тепла Q. Но энтропия при этом у первого тела уменьшится на меньшую величину, чем она увеличится у второго тела, которое принимает теплоту, так как S = Q/T (температура в знаменателе!). То есть, в результате этого самопроизвольного процесса энтропия системы из двух тел станет больше суммы энтропий этих тел до начала процесса. Иначе говоря, самопроизвольный процесс передачи тепла от тела с более высокой температурой к телу с более низкой привел к тому, что энтропия системы из этих двух тел увеличилась!

Заметим, что, рассматривая эту систему из двух тел, мы подразумевали, что внешнего теплопритока в нее или теплооттока из нее нет — то есть, считали ее изолированной (или замкнутой). Отсюда еще одна формулировка второго закона термодинамики: "при прохождении в изолированной системе самопроизвольных процессов энтропия системы возрастает". Или: "энтропия изолированной системы стремится к максимуму", так как самопроизвольные процессы передачи тепла всегда будут происходить, пока есть перепады температур.

А что будет, если наша система из двух тел не будет изолирована и, допустим, в нее поступает тепло? Ясно, что ее энтропия будет увеличиваться еще больше, так как при получении телом тепла энтропия его увеличивается ( S = Q/T).

Но для простоты формулировки этот момент обычно не упоминают, поэтому формулируют второй закон термодинамики именно для изолированных систем. Хотя, как мы видим, он действует также и для открытых систем в случае поступления в них тепла.

Третье начало термодинамики

Третье начало термодинамики связано с нахождением химического сродства — величины, характеризующей способность различных веществ химически реагировать друг с другом. Эта величина определяется работой W химических сил при реакции. Первое и второе начала термодинамики позволяют вычислить химическое сродство W только с точностью до некоторой неопределенной функции. Для определения этой функции в дополнение к обоим началам термодинамики нужны новые опытные данные о свойствах тел. В связи с этим Нернст провел экспериментальные исследования поведения веществ при низкой температуре.

На основе этих исследований и было сформулировано третье начало термодинамики, или теорема Нернста – Планка.

Энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина.

Это утверждение относится к любой равновесной системе. При Т, стремящейся к 0 К, энтропия не зависит от значения любого параметра системы. Согласно третьему началу термодинамики:

lin [S (T, X₂) - S (T, X₁)] = 0

или

lim [dS/dX]_T = 0 при Т 0,

где Х — любой термодинамический параметр (а_i или А_i).

Для всех систем предельное значение энтропии одно и то же, поэтому в нем нет никакого физического смысла, оно принимается равным нулю (постулат Планка). На основе опытов Нернста энтропия по своему существу определена с точностью до некоторой постоянной (подобно, например, электростатическому потенциалу системы зарядов в какой-либо точке поля). Значит, нет смысла вводить некую “абсолютную энтропию”, как это делал Планк и другие ученые.