Конспект лекций
по дисциплине «Процессы и аппараты химической технологии»
по направлению 240000 «Химическая и биотехнология»
специальности 240500 «Технология переработки пластических масс и эластомеров»
и специализации 240502 «Химия и технология переработки эластомеров»
для студентов специальности 240502 «Технология переработки пластических масс и эластомеров»
(заочная форма обучения)
Омск 2012
«Процессы и аппараты химической технологии»
Лекция №1
Техническая гидродинамика
В химической промышленности широко распространены процессы перемещения жидкостей, газов и паров, а также их хранения.
Техническая гидравлика является наукой о равновесии и движении жидкости (гидростатика, гидродинамика).
Гидродинамические закономерности в значительной степени определяют ход процессов теплопередачи, массопередачи и химических реакций в химических аппаратах.
Движение жидкостей и газов характеризуются одними и теми же законами, поэтому в гидравлике под жидкостью понимают как собственно жидкость, так и газы.
Под жидкостью понимают вещества, обладающие текучестью. Данные вещества не способны сохранять свою форму и полностью заполняют занимаемый ими объём.
Давление в жидкости и газе
Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности, называется давлением. За единицу давления принимается такое давление, которое производит сила в 1 Н, действующая на поверхность площадью 1 м2 перпендикулярно этой поверхности. Следовательно, чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь поверхности.
Известно, что молекулы газа беспорядочно движутся. При своем движении они сталкиваются друг с другом, а также со стенками сосуда, в котором находится газ. Молекул в газе много, потому и число их ударов очень велико. Например: число ударов молекул воздуха, находящегося в комнате, на поверхность площадью 1 см2 за 1 с выражается двадцатитрехзначным числом. Хотя сила удара отдельной молекулы мала, но действие всех молекул о стенки сосуда значительно, оно и создает давление газа.
Итак, давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа.
При уменьшении объема газа его давление увеличивается, а при увеличении объема — уменьшается, если масса и температура газа остаются неизменными.
Давление, производимое на жидкость или газ, передается без изменения в каждую точку объема жидкости или газа (закон Паскаля).
На основе закона Паскаля легко объяснить следующий опыт.
Возмём полый шар, имеющий в различных местах узкие отверстия. К шару присоединена трубка, в которую вставлен поршень. Если набрать воды в шар и вдвинуть в трубку поршень, то вода польется из всех отверстий шара. В этом опыте поршень давит на поверхность воды в трубке. Частицы воды, находящиеся под поршнем, уплотняясь, передают его давление другим слоям, лежащим глубже. Таким образом, давление поршня передается в каждую точку жидкости, заполняющей шар, и часть воды выталкивается из шара в виде струек, вытекающих из всех отверстий.
Если шар заполнить дымом, то при вдвигании поршня в трубку из отверстий шара начнут выходить струйки дыма. Этот опыт подтверждает, что газ передает производимое на него давление во все стороны одинаково.
Опустим трубку с резиновым дном, в которую налита вода, в более широкий сосуд с водой. Мы увидим, что по мере опускания трубки резиновая пленка постепенно выпрямляется. Полное выпрямление пленки показывает, что силы, действующие на нее сверху и снизу, равны. Полное выпрямление пленки наступает тогда, когда уровни воды в трубке и сосуде совпадают.
Итак, опыт показывает, что внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям. С глубиной давление увеличивается. Газы в этом отношении не отличаются от жидкостей.
Мембранный манометр
Как измерить давление жидкости на поверхность твердого тела? Как измерить, например, давление воды на дно стакана? Дно стакана деформируется под действием сил давления. Зная величину деформации, мы могли бы определить величину вызвавшей ее силы и рассчитать давление, но эта деформация настолько мала, что измерить ее практически невозможно. Поскольку судить по деформации данного тела о давлении, оказываемом на него жидкостью, удобно лишь в том случае, когда деформация достаточно велика, то для практического определения давления жидкости пользуются специальными приборами — манометрами, в которых деформации имеют сравнительно большую, легко измеримую величину.
Простейший мембранный манометр устроен следующим образом. Тонкая упругая пластинка (мембрана) герметически закрывает пустую коробку. К мембране присоединен указатель, вращающийся около оси. При погружении прибора в жидкость мембрана прогибается под действием сил давления, ее прогиб передается в увеличенном виде указателю, передвигающемуся по шкале. Каждому положению указателя соответствует определенный прогиб мембраны, а, следовательно, и определенная сила давления на мембрану. Зная площадь мембраны, можно от сил давления перейти к самим давлениям. Можно непосредственно измерять давление, если заранее проградуировать манометр, т.е. определить, какому давлению соответствует то или иное положение указателя на шкале. Для этого нужно подвергнуть манометр действию давлений, величина которых известна, и, замечая положение стрелки указателя, проставить соответственные цифры на шкале прибора.
Воздушную оболочку, окружающую Землю, называют атмосферой (гр. atmos пар, воздух и sphaire шар).
Атмосфера, как показали наблюдения за полетом искусственных спутников Земли, простирается на высоту нескольких тысяч километров. Мы живем на дне огромного воздушного океана. Поверхность Земли — дно этого океана.
Вследствие действия силы тяжести верхние слои воздуха, подобно воде океана, сжимают нижние слои. Воздушный слой, прилегающий непосредственно к Земле, сжат больше всего и согласно закону Паскаля передает производимое на него давление по всем направлениям.
В результате этого земная поверхность и тела, находящиеся на ней, испытывают давление всей толщи воздуха, или атмосферное давление.
В практике для измерения атмосферного давления используют металлический барометр, называемый анероидом (гр. a…, an… — начальная часть слова со значением отрицания; neros влажный; eidos вид). Анероид — один из видов барометра, в котором изменения атмосферного давления определяются по деформации металлической коробки с сильным разрежением внутри.
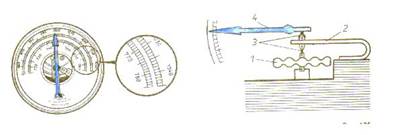
Внешний вид анероида изображен на рисунке. Главная его часть — металлическая коробочка 1 с волнистой (гофрированной) поверхностью. Из этой коробочки выкачан воздух, а чтобы атмосферное давление не раздавило ее, крышку оттягивают вверх пружиной 2. При увеличении атмосферного давления крышка прогибается вниз и натягивает пружину. При уменьшении давления пружина выпрямляет крышку. К пружине с помощью передаточного механизма 3 прикреплена стрелка-указатель 4, которая передвигается вправо или влево при изменении давления. Под стрелкой укреплена шкала, деления которой нанесены по показаниям ртутного барометра. Так, число 750, против которого стоит стрелка анероида, показывает, что в данный момент в ртутном барометре высота ртутного столба 750 мм. Следовательно, атмосферное давление равно 750 мм рт. ст., или 1000 гПа.
Знание атмосферного давления весьма важно для определения погоды на ближайшие дни, так как изменение атмосферного давления связано с изменением погоды. Барометр — необходимый прибор при метеорологических наблюдениях.
Лекция №3
Лекция №4
Основы теплопередачи
Перенос теплоты
Решающую роль в восприятии окружающего мира играют характеристики, сохраняющиеся в замкнутых системах: масса, количество движения, момент количества движения, энергия и энтропия.
В учении о теплообмене рассматриваются процессы распространения теплоты в твердых, жидких и газообразных телах. Эти процессы по своей физико-механической природе весьма многообразны, отличаются большой сложностью и обычно развиваются в виде целого комплекса разнородных явлений.
Перенос теплоты может осуществляться тремя способами: теплопроводностью, конвекцией и излучением, или радиацией. Эти формы глубоко различны по своей природе и характеризуются различными законами.
Процесс переноса теплоты теплопроводностью происходит между непосредственно соприкасающимися телами или частицами тел с различной температурой. Учение о теплопроводности однородных и изотропных тел опирается на весьма прочный теоретический фундамент. Оно основано на простых количественных законах и располагает хорошо разработанным математическим аппаратом. Теплопроводность представляет собой молекулярный процесс передачи теплоты.
При определении переноса теплоты теплопроводностью в реальных телах встречаются известные трудности, которые на практике до сих пор удовлетворительно не решены. Эти трудности состоят в том, что тепловые процессы развиваются в неоднородной среде, свойства которой зависят от температуры и изменяются по объему; кроме того, трудности возникают с увеличением сложности конфигурации системы.
Уравнение теплопроводности имеет вид:
 ;
; 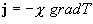 . (1)
. (1)
Оно выражает тот факт, что изменения теплосодержания определенной массы вещества, заключенного в единице объема, определяются различием между притоком и вытеканием энергии (дивергенцией плотности теплового потока j) при условии, что внутренних источников энергии нет. Тепловой поток пропорционален градиенту температуры и направлен в сторону ее падения; x — коэффициент теплопроводности.
При разработке методов исследования композиционных материалов весьма трудно и, по-видимому, не имеет смысла (в тех случаях, когда это можно практически реализовать) полностью учитывать структуру композита. В связи с этим возникла необходимость связать механику композитных материалов с механизмами элементов конструкций, развивающимися обычно в рамках континуальных процессов. Эта задача решается в процессе создания теории определения приведенных свойств композитных материалов различных структур (слоистые, волокнистые и др.) при описании их поведения в рамках континуальных представлений. Совершается переход от кусочно-однородной среды к однофазной.
Рассмотрим двухфазный композитный материал, представляющий собой матрицу, в которой случайным образом распределены включения второй фазы — армирующий элемент, имеющий приблизительно равноосную форму. Количество включений достаточно велико на участке изменения температуры. Пусть некая характеристика матрицы — А1, а включений — А2. Тогда можно представить композит как новый материал с промежуточными характеристиками между характеристиками матрицы и включений.
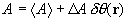 , (2)
, (2)
где 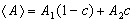 ,
, 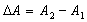 ,
, 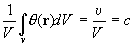 .
.
Подстановка (2) в (1) дает:
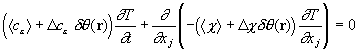 . (3)
. (3)
Имеем операторы:
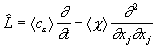 ; (4а)
; (4а)
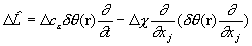 . (4б)
. (4б)
После преобразования Фурье получаем:
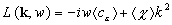 ;
;
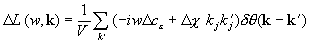 .
.
Уравнение для функции Грина:
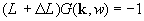 и
и 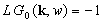 ,
,
где 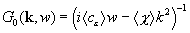 . (5)
. (5)
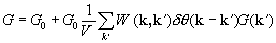 — уравнение Дайсона. (6)
— уравнение Дайсона. (6)
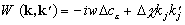 .
.
Функция Грина G0 описывает однородный материал со средними характеристиками, определяемыми по правилу смесей (2), а оператор W (k, k') можно назвать оператором возмущения, поскольку он определяет форму и расположение неоднородностей.
Решим уравнение итерациями:
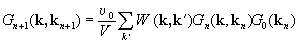 .
.
Вычислим сначала W2 (k, k2):
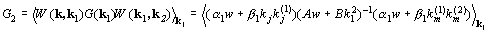 .
.
Здесь 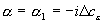 ,
, 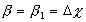 ,
, 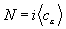 ,
, 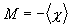 .
.
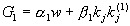 ;
;
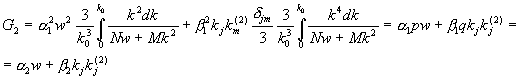 ;
;
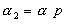 ,
, 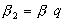 ,
, 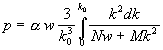 ,
, 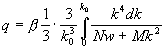 . (7)
. (7)
Теперь определим:
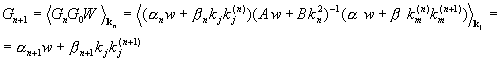 ;
;
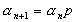 ,
, 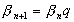 ,
, 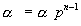 ,
, 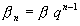 ,
, 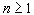 .
.
Теперь необходимо вычислить:
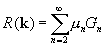 ;
;
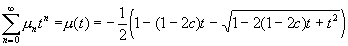 ;
;
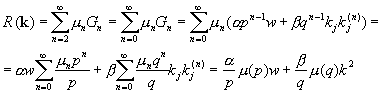 .
.
Таким образом,
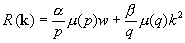 . (8)
. (8)
Подставляем в (6) равенство (8):
 ;
;
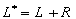 , где
, где 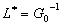 и
и 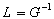 . (9)
. (9)
Подставляем (5) в (9):
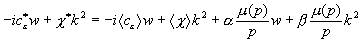 .
.
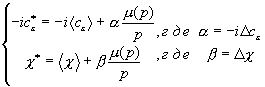 ;
;
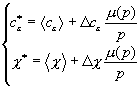 .
.
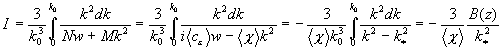 ,
,
где 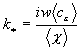 и
и 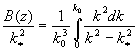 ;
;
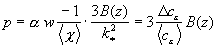 . (10)
. (10)
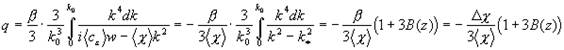 (11),
(11),
где 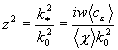 ;
; 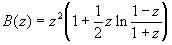 ; (12)
; (12)
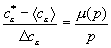 ;
;
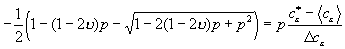 ;
;
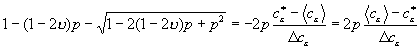 ;
;
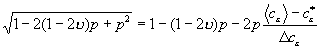
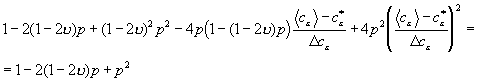 ;
;
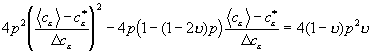 ;
;
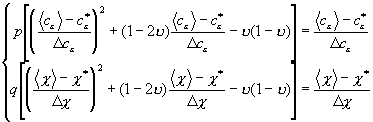 . (13)
. (13)
Ограничимся первым приближением:
` 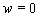 ,
, 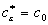 ,
, 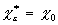 ,
,
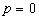 ,
, 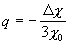 ,
, 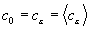 . (14)
. (14)
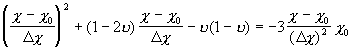 ;
;
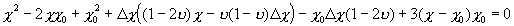 .
.
Рассмотрим:
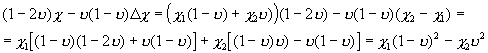 ;
;
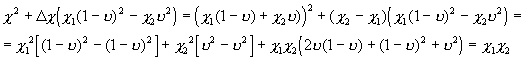 ;
;
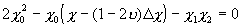 ;
;
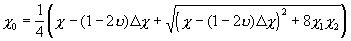 . (15)
. (15)
Ограничимся вторым приближением:
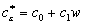 ,
, 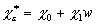 . (16)
. (16)
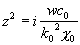 ,
, 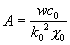 . (17)
. (17)
Из (12) найдем:
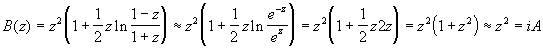 . (18)
. (18)
Подставляя (18) с учетом (16) в (10), получим:
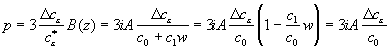 . (19)
. (19)
Теперь подставляем (19) с учетом (16) в (13), получим:
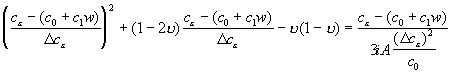 ;
;
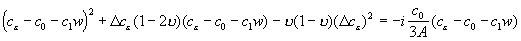 ;
;
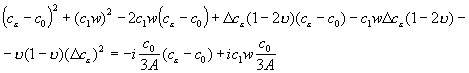 .
.
Коэффициентами при 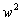 ,
, 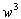 из-за малости произведения пренебрегаем, а коэффициенты без
из-за малости произведения пренебрегаем, а коэффициенты без 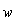 обращаются в 0 из-за (14):
обращаются в 0 из-за (14):
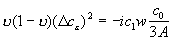 ,
,
подставляя (17), найдем:
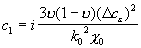 . (20)
. (20)
Подставляя (18) в (11) с учетом (16), получим:
Теперь подставляем (21) с учетом (16) в (13), получим:
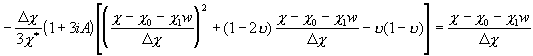
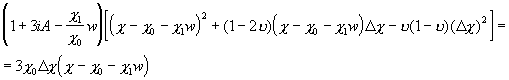 .
.
Коэффициентами при 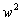 ,
, 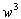 из-за малости произведения пренебрегаем, а коэффициенты без
из-за малости произведения пренебрегаем, а коэффициенты без 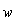 обращаются в 0 из-за (15):
обращаются в 0 из-за (15):
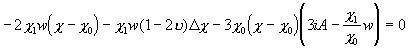 ;
;
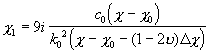 . (22)
. (22)
Ограничимся третьим приближением:
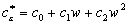 ,
, 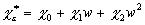 . (23)
. (23)
Подставляя (18) с учетом (23) в (10), получим:
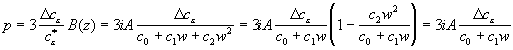 . (24)
. (24)
Теперь подставляем (24) с учетом (23) в (13), получим:
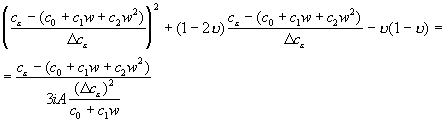 ;
;
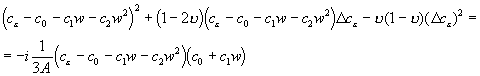 ;
;
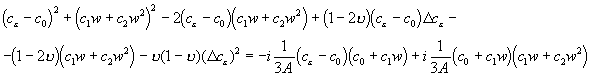 .
.
Коэффициентами при 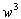 ,
, 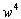 ,
, 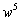 из-за малости произведения пренебрегаем, а коэффициенты без
из-за малости произведения пренебрегаем, а коэффициенты без 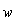 обращаются в 0 из-за (14), а с
обращаются в 0 из-за (14), а с 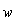 — из-за (18):
— из-за (18):
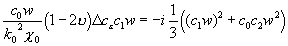 ;
;
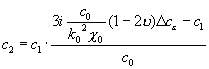 . (25)
. (25)
Подставляя (18) в (11) с учетом (23), получим:
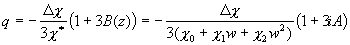 . (26)
. (26)
Теперь подставляем (26) с учетом (23) в (13), получим:
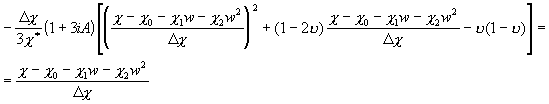 ;
;
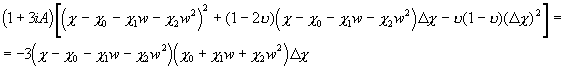 .
.
Коэффициентами при 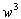 ,
, 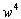 ,
, 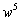 из-за малости произведения пренебрегаем, а коэффициенты без
из-за малости произведения пренебрегаем, а коэффициенты без 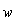 обращаются в 0 из-за (15), а с
обращаются в 0 из-за (15), а с 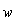 — из-за (22):
— из-за (22):
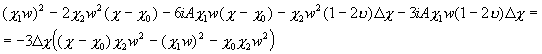 ;
;
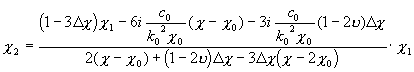 . (27)
. (27)
Анализ с1, с2, с3 и x0, x1, x2 показывает, что c0, c2 и x0, x2 — действительные коэффициенты, а c1, x1 — мнимые.
Физический смысл увеличения коэффициента теплоотдачи с увеличением скорости жидкости (газа).
Рассмотрим процесс теплоотдачи от потока теплоносителя к продольно омываемой им пластине. Скорость и температура набегающего потока постоянны и равны w ж и t ж (рис. 2.1).
Частицы жидкости, непосредственно соприкасающиеся с поверхностью, адсорбируются («прилипают») к ней. Соприкасаясь с неподвижным слоем, тормозятся и более удаленные от поверхности слои жидкости. Зона потока, в которой наблюдается уменьшение скорости (w<wж), вызванное вязким взаимодействием жидкости с поверхностью, называется гидродинамическим пограничным слоем. За пределами пограничного слоя течет невозмущенный поток. Четкой границы между ними нет, так как скорость w по мере удаления от поверхности постепенно (асимптотически) возрастает до wж. Практически за толщину гидродинамического пограничного слоя условно принимают расстояние от поверхности до точки, в которой скорость w отличается от скорости невозмущенного потока wж, незначительно (обычно на 1 %).
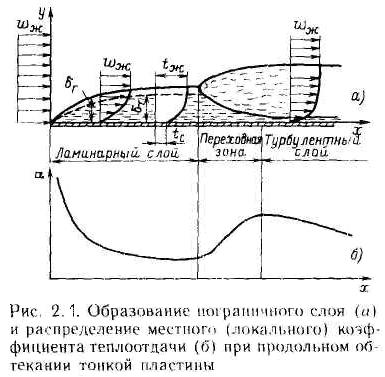 На начальном участке (при малых значениях х) гидродинамический слой очень тонок (в лобовой точке с координатой х=0 толщина равна нулю) и течение в нем ламинарное — струйки жидкости движутся параллельно, не перемешиваясь. При удалении от лобовой точки толщина пограничного слоя растет. На некотором расстоянии х = хkp ламинарное течение становится неустойчивым. В пограничном слое появляются вихри (турбулентные пульсации скорости). Постепенно турбулентный режим течения распространяется почти на всю толщину гидродинамического пограничного слоя. Лишь около самой поверхности пластины в турбулентном пограничном слое сохраняется тонкий ламинарный, или вязкий, подслой, где скорость невелика и силы вязкости гасят турбулентные вихри.
На начальном участке (при малых значениях х) гидродинамический слой очень тонок (в лобовой точке с координатой х=0 толщина равна нулю) и течение в нем ламинарное — струйки жидкости движутся параллельно, не перемешиваясь. При удалении от лобовой точки толщина пограничного слоя растет. На некотором расстоянии х = хkp ламинарное течение становится неустойчивым. В пограничном слое появляются вихри (турбулентные пульсации скорости). Постепенно турбулентный режим течения распространяется почти на всю толщину гидродинамического пограничного слоя. Лишь около самой поверхности пластины в турбулентном пограничном слое сохраняется тонкий ламинарный, или вязкий, подслой, где скорость невелика и силы вязкости гасят турбулентные вихри.
Аналогичным образом осуществляется и тепловое взаимодействие потока с пластиной. Частицы жидкости, «прилипшие» к поверхности, имеют температуру, равную температуре поверхности t с. Соприкасающиеся с этими частицами движущиеся слои жидкости охлаждаются, отдавая им свою теплоту. От соприкосновения с этими слоями охлаждаются следующие более удаленные от поверхности слои потока — так формируется тепловой пограничный слой, в пределах которого температура меняется от tc на поверхности до t ж в невозмущенном потоке. По аналогии с гидродинамическим пограничным слоем толщина теплового пограничного слоя δт принимается равной расстоянию от поверхности до точки, в которой избыточная температура жидкости V = t — lc отличается от избыточной температуры невозмущенного потока V ж = t ж — lc на малую величину (обычно на 1 %).
С удалением от лобовой точки количество охлаждающейся у пластины жидкости увеличивается, и толщина теплового пограничного слоя возрастает аналогично возрастанию δт. В общем случае толщины теплового и гидродинамического слоев не равны, но часто достаточно близки друг к другу, особенно в газах.
При ламинарном течении тепловой поток от охлаждающейся в пограничном слое жидкости переносится к поверхности пластины только за счет теплопроводности. При этом плотность теплового потока по толщине пограничного слоя неодинакова: на внешней границе q =0, ибо дальше жидкость не охлаждается; по мере приближения к поверхности значение q возрастает. Для качественного анализа можно предположить, что плотность теплового потока q по всей толщине пограничного слоя такая же, как и у поверхности. Это условие соответствует задаче о переносе теплоты теплопроводностью через плоскую стенку (пограничный слой толщиной δт с температурами tc и tж на поверхностях).
С увеличением толщины теплового пограничного слоя при ламинарном течении жидкости у поверхности пластины интенсивность теплоотдачи уменьшается. В переходной зоне общая толщина пограничного слоя продолжает возрастать, однако значение α при этом увеличивается, потому что толщина ламинарного подслоя убывает, а в образующемся турбулентном слое тепло переносится не только теплопроводностью, но и конвекцией вместе с перемещающейся массой, т. е. более интенсивно. В результате суммарное термическое сопротивление теплоотдачи убывает.
После стабилизации толщины ламинарного подслоя в зоне развитого турбулентного режима коэффициент теплоотдачи вновь начинает убывать из-за возрастания общей толщины пограничного слоя.
При течении жидкости в трубе толщина пограничного слоя вначале растет симметрично по всему периметру, как на пластине (рис. 4.4а), до тех пор, пока слои с противоположных стенок не сольются на оси трубы. Дальше движение стабилизируется и фактически гидродинамический (аналогично и тепловой) пограничный слой заполняет все сечение трубы. В зависимости от конкретных условий пограничный слой на начальном участке может успеть перейти в турбулентный, а может и не успеть. Соответственно стабилизированный режим течения в трубе будет либо турбулентным с ламинарным подслоем около стенки, либо ламинарным по всему сечению.
В связи с особенностями течения жидкости в трубе изменяется и само понятие коэффициента теплоотдачи. Для пластины коэффициент а рассчитывался как отношение плотности теплового потока q к разности температур внешнего невозмущенного потока и поверхности (или наоборот при t с > t ж). В трубе пограничный слой занимает все сечение и невозмущенного потока нет, поэтому под коэффициентом теплоотдачи понимают отношение плотности теплового потока q к разности температуры стенки и среднемассовой температуры жидкости, протекающей через данное сечение трубы. Экспериментально среднемассовая температура жидкости определяется измерением ее температуры после хорошего перемешивания.
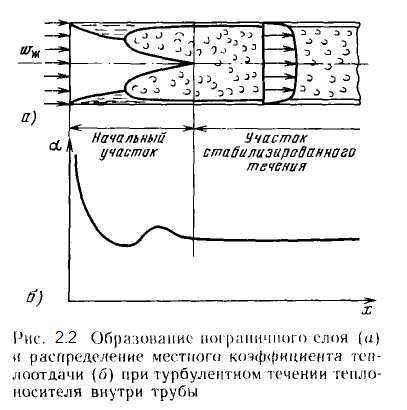 Локальный коэффициент теплоотдачи от трубы к текущей в ней жидкости изменяется лишь на начальном участке (рис. 4.4б), а на участке стабилизированного течения αст = const, поскольку толщина пограничного слоя (δт= r) постоянна. С увеличением скорости течения теплоносителя в трубе αст возрастает из-за уменьшения толщины ламинарного подслоя, а с увеличением диаметра трубы уменьшается, поскольку растет толщина всего пограничного слоя δт= r .
Локальный коэффициент теплоотдачи от трубы к текущей в ней жидкости изменяется лишь на начальном участке (рис. 4.4б), а на участке стабилизированного течения αст = const, поскольку толщина пограничного слоя (δт= r) постоянна. С увеличением скорости течения теплоносителя в трубе αст возрастает из-за уменьшения толщины ламинарного подслоя, а с увеличением диаметра трубы уменьшается, поскольку растет толщина всего пограничного слоя δт= r .
Критерии подобия при подсчете величин коэффициентов теплоотдачи
При подсчете величин коэффициентов теплоотдачи применяются основные критерии подобия:
Критерий Прандтля:

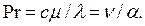
Критерий Рейнольдса:
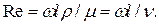
Критерий Галилея:
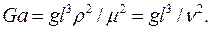
Критерий Грасгофа:
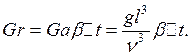
Критерий Пекле:
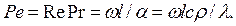
Лекция №5
Теплообменные аппараты
Кожухотрубчатые теплообменники могут использоваться в качестве холодильниковконденсаторов и испарителей.
На рис изображон кожухотрубчатый двухходовой по трубному пространству пространству горизонтальный холодильник предназначенный для теплообмена между теплоносителями без изменения их агрегатного состояния .В соответствии с ГОСТ 15120-79 и ГОСТ 15122-79 Кожухотрубчатые холодильники могут быть двух типов Н-с неподвижными трубными решотками и К- с линзовым компенсатором неодинаковых температурных удлинений кожуха и труб .Наибольшая допускаемая разность температур кожуха и труб для холодильников типа Н может составлять от 20 до 60 град в зависимости от материала труб и кожуха от давления в кожухе и от диаметра аппарата
Холодильники могут устанавливаться горизонтально и вертикально быть одно- двух- четырех- и шестиходовыми по трубному пространству . Трубы могут быть изготовлены из углеродестой или нержавеющей стали а по ГОСТ 15120-79-также из латуни. Кожух распределительные камеры и крышки изготовляют из углеродистой или нержавеющей стали.
Поверхность теплопередачи нормализованных теплообменников а также параметры конструкции необходимые для уточненного определения требуемой поверхности гидровлического сопротивления и массы аппаратов.
Кожухотрубчатые конденсаторы предназначены для конденсации паров веществ в межтрубном пространстве а также для подогрева жидкостей и газов за счет тепла конденсации пара. Они могут быть с неподвижной трубной решеткой или с температурным компенсатором на кожухе вертикальные или горизонталные. В соответствии с ГОСТ 15121-79 конденсаторы могут быть двух- четырех- и шестиходовыми по трубному пространству. От холодильников они отличаются большим диаметром штуцера для подвода пара в межтрубное пространство.
В кожухотрубчатых испарителях в трубном пространстве кипит жидкость а в межтрубном пространстве может быть жидкий газообразный парообразныйпарогазовый или парожидкостной теплоноситель. Эти теплообменники в соответствии с ГОСТ 15119-79 могут быть только вертикальными и одноходовыми с трубками диаметром 25· 2мм.Они могут быть с неподвижной трубной решеткой или с температурным компенсатором на кожухе . Основные параметры кожухотрубчатых конденсаторов и испарителей в соответствии с ГОСТ 15118-79, 15119-79 и 15121-79 .
Применение кожухотрубчатых теплообменников с температурным компенсатором на кожухе (линзовый компенсатор) ограничено предельно допустимым давлением в кожухе, равным 1,6 МПа. При большем давлением в кожухе (от 1,6 до 8,0 МПа) следует применять теплообменники с плавающей головкой или с U-образными трубами.
На рис. изображен кожухотрубчатый холодильник с плавающей головкой, предназначенный для охлождения (нагревания) жидких или газообразных сред без изменения их агрегатного состояния. Не закрепленная на кожухе вторая трубная решетка вместе с внутренней крышкой, отделяющей трубное пространство от межтрубного, образуют так называемую плавающую головку. Такая конструкция исключает температурные напряжения в кожухе и трубах. Эти теплообменники нормализованные с соответствии с ГОСТ 14246-79 ,
могут быть двух или четырехходовыми, горизонтальными, длиной 3, 6 и 9 м или вертикальными 3м. Поверхности теплопередачи и основные параметры сведены в таблицы.
Кожухотрубчатые конденсаторы с плавающей головкой (ГОСТ 14247-79) отличаются от аналогичных холодильников большим диаметром штуцера для подвода пара в межтрубное пространство. Допустимое давление охлаждающей среды в трубах до 1,0 МПа, в межтрубном пространстве-от 1,0до 2,5МПа. Эти теплообменники могут быть двух- четырех- и шестиходовыми по трубному пространству. Диаметр кожуха от 600 до 1400 мм, высота труб 6,0м. Поверхности теплопередачи и основные параметры их также представлены в табл.
Теплообменники с U-образными трубами применяют для нагрева и охлаждения жидких или газообразных сред без изменения их агрегатного состояния. Они рассчитаны на давление до 6,4МПа, отличаются от холодильников с плавающей головкой менее сложной конструкцией (однотрубная решетка, нет внутренней крышки), однако могут быть лишь двухходовыми из труб только одного сортамента -:20 *2мм. Поверхности теплообмена и основные параметры этих теплообменников в соответствии с ГОСТ 14245-79 приведены в таблицах.
Кожухотрубчатые испарители с трубными пучками из U-образных труб или с плавающей головкой имеют паровое пространство над кипящей в кожухе жидкостью. В этих аппаратах, расположенных всегда горизонтально, горячий теплоноситель (в качестве которого могут использоваться газы, жидкости или пар) движется по трубам. Согласно ГОСТ 14248-79, кожухотрубчатые испарители могут быть с коническим днищем диаметром от 800 до 1600 мм и с эллиптическим днищем диаметром от 2400 до 2800мм. Последние могут иметь два или три трубных пучка. Допустимые давления в трубах составляют от 1,6 до 4,0 МПа, в кожухе – от 1,0 до 2,5 МПа при рабочих температурах от -30до 450С, т.е. выше, чем для испарителей с линзовым компенсатором. Испарители с паровым пространством изготовляют лишь двухходовыми, только из труб длиной 6,0 м, диаметром 25*2мм. Поверхности теплообмена и основные параметры испарителей с паровым пространством в соответствии с ГОСТ14248-79.
Лекция №6
Сушильные процессы
Сушильные установки
Влажность воздуха
Вода в атмосфере содержится в виде молекул (пар), капелек и кристалликов, влажность воздуха характеризуется содержанием водяного пара в г/м3 (абсолютная влажность — “а” 4м3) или упругостью- “с” мм р.с., мб, г.п). Количество водяного пара, которое может содержаться в воздухе при данной температуре, — максимальное влагосодержание (или максимальная упругость) водяного пара (Е). Процентное отношение количества водяного пара, содержащегося в воздухе, к тому количеству, которое может содержаться при данной температуре, — относительная влажность (%). Она показывает степень насыщения воздуха водяным паром.
Разность между максимальной (Е) и фактической упругостью водяного пара — дефицит 4 (Д). Температура, при которой находящийся в воздухе водяной пар насытит его и начнется конденсация, — точка росы (Т0). Чем выше температура воздуха, тем больше водяного пара он может содержать и тем выше точка росы.
Водяной пар поступает в атмосферу в результате процесса испарения с поверхности. Испарение зависит от температуры испаряющей поверхности и от относительной влажности воздуха. Насыщенный воздух не может вместить больше пара, если температура его не повысится. При повышении температуры он удаляется от насыщения, при понижении, наоборот, в нем может начаться конденсация. Так происходит, например, летней ночью при ясной погоде, соприкасаясь с холодной поверхностью, воздух оставляет на ней капельки росы. При отрицательной температуре выпадает иней. В воздухе, охлаждающемся от поверхности или от пришедшего холодного воздуха, образуется туман. Он состоит из мелких капелек или кристалликов, взвешенных в воздухе. В сильно загрязнённом воздухе образуется густой туман с примесью дыма — смог.
Облака образуются при конденсации водяного пара в поднимающемся воздухе вследствие его охлаждения. Высота их образования зависит от температуры и относительной влажности воздуха. При достижении им высоты, на которой насыщение станет полным (100%), начинается конденсация и облакообразование. Если восходящий воздух встретит теплый слой (инверсия), подъём прекращается, воздух не достигает границы конденсации и облака не образуются.
Облака находятся в постоянном движении, опускаясь ниже границы конденсации, они испаряются (“тают”). Облака могут состоять из мелких капелек или кристалликов, чаще всего они смешанные. По форме (по виду) различают облака перистые, слоистые и кучевые. Перистые облака — облака верхнего яруса (выше 6000 м), полупрозрачные, ледяные. Осадки из них не выпадают. Слоистые облака среднего (от 2000 до 6000 м) и нижнего (ниже 2000 м) ярусов. В основном они и дают осадки, обычно длительные, обложные. Кучевые облака могут образоваться в нижнем ярусе и достигать очень большой высоты. Часто они имеют вид башен и состоят внизу из капелек, вверху — из кристалликов. С ними связаны ливни, град, грозы. Кроме трёх основных форм облаков, возникает много комбинированных. Например, перисто-слоистые, слоисто-кучевые, перисто-кучевые и.т. д.
Форма облаков объясняется их происхождением. Облачный покров обычно состоит из разных облаков. Степень покрытия неба облаками — облачность — измеряется в баллах. Полная облачность — 10 баллов. В среднем на Земле половина неба закрыта облаками. Наибольшая облачность там, где воздух поднимается, то есть в облаках пониженного давления. Наименьшая облачность — соответственно, в областях повышенного давления. Над океаном она больше, чем над сушей, так как там больше влаги в воздухе. Абсолютный максимум облачности — над Северной Атлантикой (9 баллов), абсолютный минимум — над Антарктидой и над тропическими пустынями (0,2 балла). Облачный покров задерживает солнечную радиацию, идущую к земной поверхности, отражает и рассеивает её. Одновременно облака задерживают тепловые излучения земной поверхности в атмосфере. Поэтому влияние облачности на климат велико.
От влажности зависит интенсивность испарения влаги с поверхности кожи человека. А испарение влаги имеет большое значение для поддержания температуры тела постоянной. В космических кораблях поддерживается наиболее благоприятная для человека относительная влажность воздуха (40 – 60%).
Большое значение имеет знание влажности в метеорологии для предсказания погоды. Хотя количество водяного пара в атмосфере сравнительно невелико (около 1%), роль его в атмосферных явлениях значительна. Конденсация водяного пара приводит к образованию облаков и последующему выпадению осадков. При этом выделяется большое количество теплоты, а испарение воды сопровождается поглощением теплоты.
В ткацком, кондитерском и других производствах для нормального течения процесса необходима определённая влажность.
Хранение произведений искусства и книг требуют поддержания влажности воздуха на необходимом уровне. Поэтому в музеях на стенах вы можете видеть психрометры.
Оптимальные нормы микроклимата для помещений с ВДТ и ВЭВМ.
| Период года | Категория робот | Температура воздуха 0С не более | Относительная влажность воздуха, % | Скорость движения воздуха, м/с |
| Холодный | легкая-19 | 22 – 24 | 40 – 60 | 0,1 |
| легкая -16 | 21 – 23 | 40 – 60 | 0,1 | |
| Тёплый | легкая -19 | 23 – 25 | 40 – 60 | 0,1 |
| легкая -16 | 22 – 24 | 40 – 60 | 0,2 |
Приложение (обязательное); оптимальные и допустимые параметры температуры и относительной влажностью воздуха в помещениях с ВДТ и ПЭВМ во всех учебных и дошкольных учреждениях.
| Оптимальные параметры | Допустимые параметры | ||
| Температура, 0С. | Относительная влажность % | Температура, 0С. | Относительная влажность % |
| 19 | 62 | 18 | 39 |
| 20 | 58 | 22 | 31 |
| 21 | 55 | ||
Лекция №8
Ректификационная установка.
Материальный баланс колонны и определение рабочего флегмового числа
Производительность колонны по дистилляту 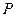 и кубовому остатку
и кубовому остатку 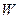 определяем из уравнений материального баланса колонны:
определяем из уравнений материального баланса колонны:
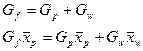 (1)
(1)
Откуда находим:
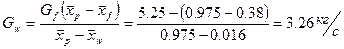 ,
,
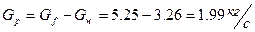 .
.
Нагрузки ректификационной колонны по пару и жидкости определяются значением рабочего флегмового числа 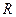 ; его оптимальное значение
; его оптимальное значение 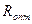 можно найти путем технико-экономического расчета. Ввиду отсутствия надежной методики оценки
можно найти путем технико-экономического расчета. Ввиду отсутствия надежной методики оценки 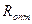 используют приближенные вычисления, основанные на определении коэффициента избытка флегмы (орошения)
используют приближенные вычисления, основанные на определении коэффициента избытка флегмы (орошения) 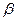 , равного отношению
, равного отношению 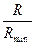 , где минимальное флегмовое число:
, где минимальное флегмовое число:
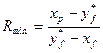 , (2)
, (2)
где 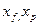 – мольные доли легколетучего компонента соответственно в исходной смеси и дистилляте,
– мольные доли легколетучего компонента соответственно в исходной смеси и дистилляте,  ;
;
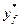 – концентрация легколетучего компонента в паре, находящемся в равновесии с исходной смесью,
– концентрация легколетучего компонента в паре, находящемся в равновесии с исходной смесью, 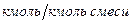 .
.
Пересчитаем составы фаз из массовых в мольные доли по соотношению
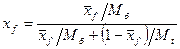 , (3)
, (3)
где 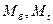 - молекулярные массы соответственно бензола и толуола,
- молекулярные массы соответственно бензола и толуола, 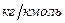 .
.
Получим:
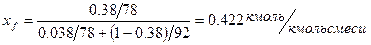 .
.
Аналогично найдем: 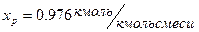 ,
, 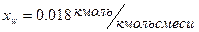 .
.
Тогда минимальное флегмовое число по формуле (2) равно:
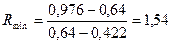 .
.
Рабочее (действительное) число флегмы:
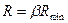 (4)
(4)
Задавшись различными значениями коэффициентов избытка флегмы 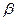 , определим соответствующие флегмовые числа.
, определим соответствующие флегмовые числа.
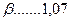
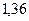
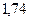
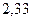

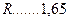
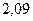
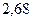
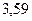
Графическим построением ступеней изменения концентраций между равновесной и рабочими линиями в диаграмме состав пара 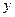 – состав жидкости
– состав жидкости 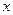 находим
находим 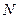 , диаграммы приведены в приложении 1. Равновесные данные для различных систем приведены в справочнике.
, диаграммы приведены в приложении 1. Равновесные данные для различных систем приведены в справочнике.
Для построения диаграммы равновесия между паром и жидкостью рассчитаем уравнения рабочих линий для верхней (укрепляющей) и нижней (исчерпывающей) части колонны.
a) верхняя часть ректификационной колонны
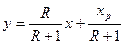 (4)
(4)
b) нижняя часть колонны
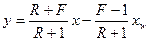 , (5)
, (5)
где 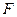 – относительный мольный расход питания.
– относительный мольный расход питания.
Относительный мольный расход питания находится по формуле:
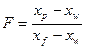 (6)
(6)
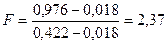
Для флегмового числа 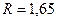 :
: 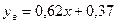 ,
, 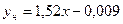 .
.
Для флегмового числа 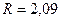 :
: 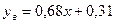 ,
, 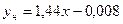 .
.
Для флегмового числа 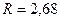 :
: 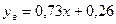 ,
, 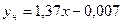 .
.
Для флегмового числа 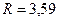 :
: 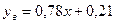 ,
, 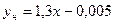 .
.
Результаты расчетов рабочего флегмового числа приведены ниже в таблице 1.
Таблица 1 – Расчет рабочего флегмового числа
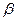
| 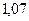
| 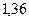
| 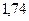
| 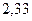
|
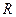
| 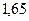
| 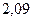
| 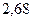
| 
|
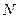
| 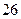
| 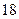
| 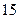
| 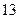
|
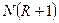
| 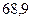
| 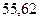
| 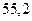
| 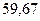
|
Для определения минимального флегмового числа построим график в координатах 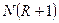 –
– 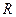 .
.
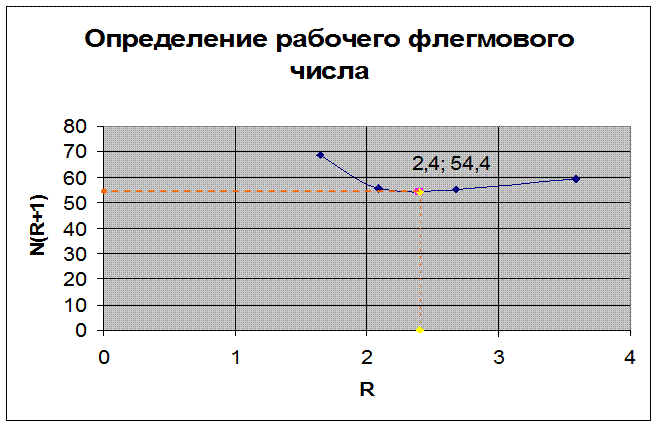
Рисунок 1 Определение рабочего флегмового числа
Минимальное произведение 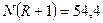 соответствует флегмовому числу
соответствует флегмовому числу 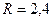 . В приложении 2 изображена диаграмма равновесия между жидкостью и паром при постоянном давлении. На диаграмме рабочие линии и ступени изменения концентраций для верхней (укрепляющей) и нижней (исчерпывающей) частей колонны в соответствии с найденным числом
. В приложении 2 изображена диаграмма равновесия между жидкостью и паром при постоянном давлении. На диаграмме рабочие линии и ступени изменения концентраций для верхней (укрепляющей) и нижней (исчерпывающей) частей колонны в соответствии с найденным числом 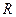 .
.
Средние массовые расходы (нагрузки) по жидкости для верхней и нижней частей колонны определяются из соотношений:
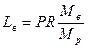 (7)
(7)
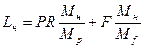 , (8)
, (8)
где  – мольные массы дистиллята и исходной смеси;
– мольные массы дистиллята и исходной смеси;
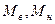 – средние мольные массы жидкости в верхних и нижних частях колонны.
– средние мольные массы жидкости в верхних и нижних частях колонны.
Мольную массу дистиллята можно принять равной мольной массе легколетучего компонента – бензола. Мольная масса жидкости в верхней и нижней частях колонны равна:
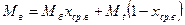 , (9)
, (9)
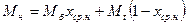 , (10)
, (10)
где 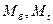 – мольные массы бензола и толуола;
– мольные массы бензола и толуола;
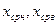 – средний мольный состав жидкости соответственно в верхней и нижней частях колонны:
– средний мольный состав жидкости соответственно в верхней и нижней частях колонны:
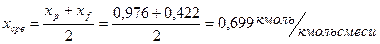 ,
,
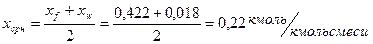 .
.
Тогда:
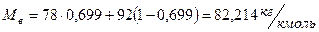 ,
,
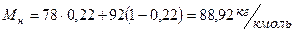 .
.
Мольная масса исходной смеси:
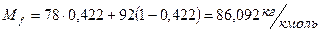 .
.
Подставив, получим:
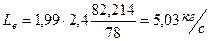 ,
,
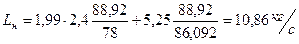 .
.
Средние массовые потоки пара в верхней 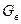 и нижней
и нижней 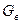 частях колонны соответственно равны:
частях колонны соответственно равны:
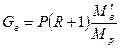 , (11)
, (11)
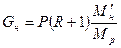 , (12)
, (12)
где 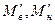 – средние мольные массы паров в верхней и нижней части колонны:
– средние мольные массы паров в верхней и нижней части колонны:
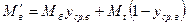 (13)
(13)
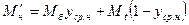 (14)
(14)
Где:
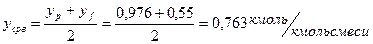 ,
,
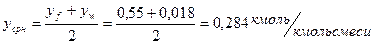 .
.
Тогда:
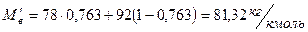 ,
,
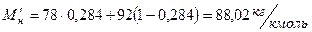 .
.
Подставив, получим:
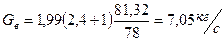 ,
,
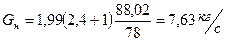 .
.
2 Определение скорости пара и диаметра колонны
Средние температуры пара определяем по диаграмме  (рис.2):
(рис.2):
a) при 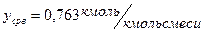
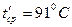 ;
;
b) при 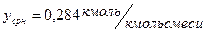
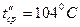 .
.
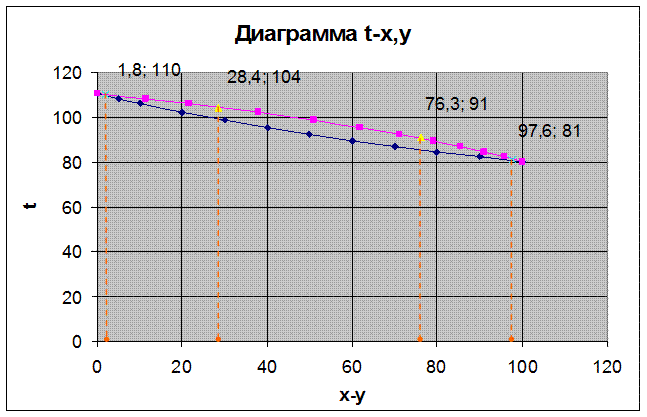
Рисунок 2 Диаграмма равновесия между паром и жидкостью - в координатах температура t - состав пара y и жидкости x
Определим плотность пара в верхней и нижней части колонны по формуле:
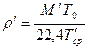 (15)
(15)
a) 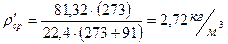 ;
;
b) 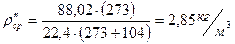 .
.
Средняя плотность пара в колонне:
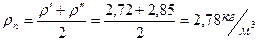 .
.
Плотности жидкого бензола и жидкого толуола близки. Температура вверху колонны при 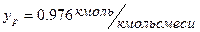 равняется
равняется 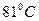 , а в кубе-испарителе при
, а в кубе-испарителе при 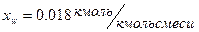 она равна
она равна 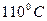 (рис.2).
(рис.2).
Плотность жидкого бензола при 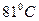
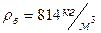 , а жидкого толуола при
, а жидкого толуола при  она равна
она равна 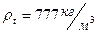 .
.
Принимаем среднюю плотность жидкости в колонне:
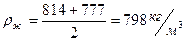 .
.
Определяем скорость пара в колонне по уравнению:
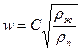 (16)
(16)
По данным каталога-справочника «Колонные аппараты» принимаем расстояние между тарелками 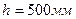 . Для ситчатых тарелок определяем коэффициент
. Для ситчатых тарелок определяем коэффициент 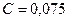 .
.
Скорость пара в колонне:
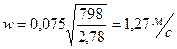 .
.
Объемный расход проходящего через колонну пара при средней температуре 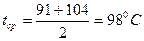 :
:
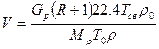 (17)
(17)
где 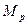 – мольная масса дистиллята.
– мольная масса дистиллята.
 .
.
Диаметр колонны:
 (18)
(18)
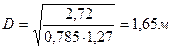 .
.
По каталогу-справочнику «Колонные аппараты» берем 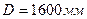 . Тогда скорость пара в колонне будет:
. Тогда скорость пара в колонне будет:
 .
.
По каталогу для колонны диаметром 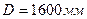 выбираем ситчатую однопоточную тарелку
выбираем ситчатую однопоточную тарелку  со следующими конструктивными размерами:
со следующими конструктивными размерами:
Диаметр отверстий в тарелке 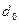 …………
………… 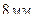
Шаг между отверстиями  ………………..
……………….. 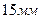
Свободное сечение тарелки 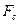 …………...
…………... 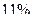
Высота переливного порога 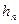 …………...
…………... 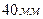
Ширина переливного порога 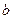
Рабочее сечение тарелки 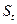 ……………….
………………. 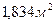
Периметр слива 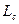 ………………………...
………………………... 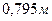
3 Гидравлический расчет тарелок
Рассчитаем гидравлическое сопротивление тарелки в верхней и нижней части колонны по уравнению:
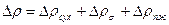 , (19)
, (19)
где 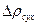 – гидравлическое сопротивление сухой тарелки;
– гидравлическое сопротивление сухой тарелки;
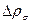 – сопротивление, обусловленное силами поверхностного натяжения;
– сопротивление, обусловленное силами поверхностного натяжения;
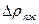 – сопротивление парожидкостного слоя на тарелке.
– сопротивление парожидкостного слоя на тарелке.
a) Верхняя часть колонны.
Гидравлическое сопротивление сухой тарелки:
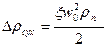 , (20)
, (20)
где 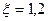 – коэффициент сопротивления ситчатых тарелок;
– коэффициент сопротивления ситчатых тарелок;
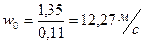 – скорость пара в отверстиях тарелки.
– скорость пара в отверстиях тарелки.
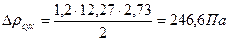 .
.
Сопротивление, обусловленное силами поверхностного натяжения:
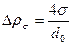 , (21)
, (21)
где 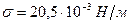 а – поверхностное натяжение жидкости при средней температуре в верхней части колонны
а – поверхностное натяжение жидкости при средней температуре в верхней части колонны  (у бензола и толуола практически одинаковое поверхностное натяжение);
(у бензола и толуола практически одинаковое поверхностное натяжение);
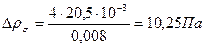 .
.
Сопротивление парожидкостного слоя на тарелке:
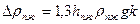 , (22)
, (22) 
где 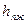 – высота парожидкостного слоя;
– высота парожидкостного слоя;
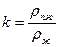 – отношение плотности парожидкостного слоя к плотности жидкости, принимаемое приближенно равным
– отношение плотности парожидкостного слоя к плотности жидкости, принимаемое приближенно равным 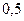 .
.
Высота парожидкостного слоя:
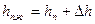 (23)
(23)
Величину 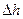 – высоту слоя над сливной перегородкой рассчитываем по формуле:
– высоту слоя над сливной перегородкой рассчитываем по формуле:
 , (24)
, (24)
где 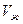 – объемный расход жидкости.
– объемный расход жидкости.
Объемный расход жидкости в верхней части колонны:
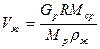 (25)
(25)
где 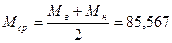 – средняя мольная масса жидкости
– средняя мольная масса жидкости 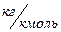 .
.
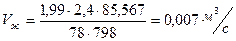 .
.
Тепловой расчет установки
Расход теплоты, отдаваемой охлаждающей воде в дефлегматоре-конденсаторе, находим по уравнению:
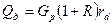
Здесь
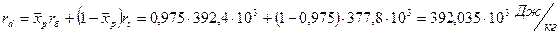 ,
,
где 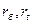 е – удельные теплоты конденсации бензола и толуола при
е – удельные теплоты конденсации бензола и толуола при 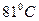 .
.
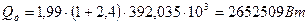 .
.
Расход теплоты получаемый в кубе-испарителе от греющего пара, находим по уравнению:
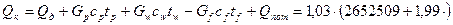
Лекция №9
Холодильные процессы.
Холодильные установки
Второй закон термодинамики
Второй закон термодинамики (как и первый — закон сохранения энергии) установлен эмпирическим путем. Впервые его сформулировал Клаузиус: "теплота сама собой переходит лишь от тела с большей температурой к телу с меньшей температурой и не может самопроизвольно переходить в обратном направлении".
Другая формулировка: все самопроизвольные процессы в природе идут с увеличением энтропии. (Энтропия — мера хаотичности, неупорядоченности системы).
Рассмотрим систему из двух контактирующих тел с разными температурами. Тепло пойдет от тела с большей температурой к телу с меньшей до тех пор, пока температуры обоих тел не выровняются. При этом от одного тела к другому будет передано определенное количество тепла  Q. Но энтропия при этом у первого тела уменьшится на меньшую величину, чем она увеличится у второго тела, которое принимает теплоту, так как
Q. Но энтропия при этом у первого тела уменьшится на меньшую величину, чем она увеличится у второго тела, которое принимает теплоту, так как  S =
S =  Q/T (температура в знаменателе!). То есть, в результате этого самопроизвольного процесса энтропия системы из двух тел станет больше суммы энтропий этих тел до начала процесса. Иначе говоря, самопроизвольный процесс передачи тепла от тела с более высокой температурой к телу с более низкой привел к тому, что энтропия системы из этих двух тел увеличилась!
Q/T (температура в знаменателе!). То есть, в результате этого самопроизвольного процесса энтропия системы из двух тел станет больше суммы энтропий этих тел до начала процесса. Иначе говоря, самопроизвольный процесс передачи тепла от тела с более высокой температурой к телу с более низкой привел к тому, что энтропия системы из этих двух тел увеличилась!
Заметим, что, рассматривая эту систему из двух тел, мы подразумевали, что внешнего теплопритока в нее или теплооттока из нее нет — то есть, считали ее изолированной (или замкнутой). Отсюда еще одна формулировка второго закона термодинамики: "при прохождении в изолированной системе самопроизвольных процессов энтропия системы возрастает". Или: "энтропия изолированной системы стремится к максимуму", так как самопроизвольные процессы передачи тепла всегда будут происходить, пока есть перепады температур.
А что будет, если наша система из двух тел не будет изолирована и, допустим, в нее поступает тепло? Ясно, что ее энтропия будет увеличиваться еще больше, так как при получении телом тепла энтропия его увеличивается (  S =
S =  Q/T).
Q/T).
Но для простоты формулировки этот момент обычно не упоминают, поэтому формулируют второй закон термодинамики именно для изолированных систем. Хотя, как мы видим, он действует также и для открытых систем в случае поступления в них тепла.
Третье начало термодинамики
Третье начало термодинамики связано с нахождением химического сродства — величины, характеризующей способность различных веществ химически реагировать друг с другом. Эта величина определяется работой W химических сил при реакции. Первое и второе начала термодинамики позволяют вычислить химическое сродство W только с точностью до некоторой неопределенной функции. Для определения этой функции в дополнение к обоим началам термодинамики нужны новые опытные данные о свойствах тел. В связи с этим Нернст провел экспериментальные исследования поведения веществ при низкой температуре.
На основе этих исследований и было сформулировано третье начало термодинамики, или теорема Нернста – Планка.
Энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина.
Это утверждение относится к любой равновесной системе. При Т, стремящейся к 0 К, энтропия не зависит от значения любого параметра системы. Согласно третьему началу термодинамики:
lin [S (T, X2) - S (T, X1)] = 0
или
lim [dS/dX]T = 0 при Т 0,
где Х — любой термодинамический параметр (аi или Аi).
Для всех систем предельное значение энтропии одно и то же, поэтому в нем нет никакого физического смысла, оно принимается равным нулю (постулат Планка). На основе опытов Нернста энтропия по своему существу определена с точностью до некоторой постоянной (подобно, например, электростатическому потенциалу системы зарядов в какой-либо точке поля). Значит, нет смысла вводить некую “абсолютную энтропию”, как это делал Планк и другие ученые.
Их основные свойства.
Для охлаждения до температур 10... 30 °С в качестве охлаждающих агентов используют доступные и дешевые — воздух и воду.
Атмосферный воздух имеет низкую теплоемкость и низкие коэффициенты теплоотдачи, но, несмотря на это, находит применение как охладитель.
По сравнению с воздухом вода имеет большую теплоемкость, больший коэффициент теплоотдачи, поэтому может забрать больше теплоты от охлаждаемой среды. В качестве охлаждающего агента используется речная, озерная, прудовая и артезианская вода. Вода естественных водоемов в зависимости от времени года имеет температуру 4...25°С, артезианская вода — 8...15°С. Если для охлаждения применяется оборотная вода, то ее температура летом может достигать 30 °С. Вода как охлаждающий агент используется главным образом в поверхностных теплообменных аппаратах (холодильниках), но может применяться и в теплообменниках смешивания. Чтобы предотвратить загрязнение поверхности теплообмена выделяемыми из воды растворенными в ней солями, температура воды на выходе из холодильника не должна превышать 40...50°С.
Если температура охлаждаемой среды выше 100 °С, то охлаждающая вода будет испаряться. Охлаждение путем испарения снижает расход воды, образующийся пар можно использовать как низкотемпературный греющий агент. Охлаждение до температур ниже 0 °С проводится с помощью холодильных агентов (хладагентов). Наиболее распространенными хладагентами являются аммиак и фреоны (фторхлорпроизводные метана).
Лекция №10
Процессы смешивания.
Конструкции мешалок.
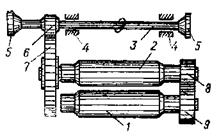
Резиновая смесь является сложной многокомпонентной системой, в состав которой входят каучуки и различные ингредиенты, равномерно распределенные в массе каучука. Для получения резиновых смесей каучук и ингредиенты смешивают до образования однородной массы.
Рис. 4. Камера резиносмесителя с овальными роторами:
1 — верхний затвор; 2 — корпус рабочей камеры; 3 — роторы; 4 — гребень нижней разгрузочной дверцы [11] .
расположены так, чтобы осевые силы, возникающие в гребнях, были направлены к середине камеры [11, 20-23].Диаметры роторов по гребням на 3 мм меньше диаметра цилиндрической камеры; зазор δ между гребнем и стенкой камеры равен 1,5 мм. При износе гребней и стенок камеры зазор увеличивается, что снижает эффективность работы оборудования. Не рекомендуется допускать увеличения зазора свыше 6 мм; зазор между гребнями роторов 3 мм. Роторы имеют фрикцию; 1:1,18. Материалы обрабатывают в четырех зазорах между гребнями роторов и неподвижными стенками камеры. Благодаря винтообразной форме гребней создается внешнее давление на обрабатываемый материал, направленное по нормали к его поверхности. Эту нормально направленную силу Nc можно разложить на три составляющие: радиальную R, оказывающую давление на корпус через материал, окружную Р и осевую А. Окружное усилие, деформируя материал, способствует его ламинарному истечению через зазоры, а осевое усилие вызывает местные турбулентные завихрения (перемещение материала к центру камеры), что способствует лучшему диспергированию компонентов.
При заполнении объема рабочей камеры на 53—65% гребни роторов несут избыточный материал, не прошедший через зазоры, к верхней части камеры и к верхнему затвору резиносмесителя. Здесь потоки встречаются, при этом создается давление, за счет которого верхний затвор (при недостаточном пневматическом давлении) поднимается, и материал входит в загрузочное окно, выбывая из общего процесса смешения. Чтобы избежать такого нежелательного явления, необходимо следить за пневматическим давлением на верхний затвор. Встречные потоки и пневматическое давление на верхний затвор в этой зоне обеспечивают эффективное перемешивание. Движением гребней в центральной части камеры материал перемещается вниз и в зазорах между гребнями роторов подвергается дополнительной обработке. Осевые силы от гребней создают местные турбулентные завихрения. При дальнейшем перемещении материал встречает неподвижный гребень 4 скользящей дверцы, расположенный параллельно осям роторов и имеющий контуры цилиндрической поверхности камеры. Этот гребень разделяет общий поток на два, каждый из которых направлен в соответствующий корпус камеры. В этой зоне в материале развиваются сдвиговые явления, усиливающиеся при наличии фрикции у роторов.
Таким образом, деформация каучука и резиновой смеси и соответственно смешение происходят во всем объеме материала и во всех частях камеры.
Проходные сечения в камере смесителя изменяются от 1,5— 4 мм между стенкой камеры и площадкой гребня лопасти до 240 мм между валками роторов. При этом для смесителя с объемом камеры 250 л при частоте вращения роторов 40 об/мин окружные скорости отдельных точек лопасти составляют 1,2 и 0,66 м/с, что обусловливает изменение скорости сдвига в весьма больших пределах и следовательно различную интенсивность диспергирования ингредиентов в различных частях смесителя.
В основном процесс диспергирования происходит в зазоре между гребнем ротора и стенками камеры, где наблюдается наибольшая скорость сдвига.
Производительность резиносмесителя П характеризуется его конструктивными и энергетическими параметрами и определяется по уравнению
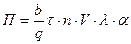 (1)[11]
(1)[11]
где b — коэффициент пропорциональности, равный 2,062-10-2;
q — удельный расход энергии, зависящий от свойств перерабатываемых материалов и конструкции смесителя;
τ— среднее сдвиговое напряжение, развивающееся в приграничном к стенке камеры слое смеси в процессе ее изготовления;
п — частота вращения ротора;
V — полный объем камеры смесителя;
λ — безразмерный коэффициент, характеризующий степень совершенства конструкции смесительного механизма и степень заполнения камеры, равен 0,2—0,6.
Для того чтобы увеличить производительность резиносмесителей, необходимо повысить частоту вращения роторов, увеличить объемы камеры смесителя, уменьшить продолжительность подготовительных операций при смешении, а также усовершенствовать конструкцию смесителя [11] .
Конструкция вальцев с групповым приводом. Техническая характеристика агрегата из 3-х машин.
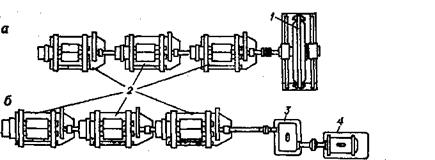
Рис. 5. Вальцы с групповым электроприводом (вид сверху) от тихоходного синхронного электродвигателя (а) и от быстроходного асинхронного электро двигателя через редуктор (б):
1 — тихоходный синхронный электродвигатель; 2 — вальцы; 3 — редуктор; 4 — быстроходный асинхронный электродвигатель [21].
Для вальцев с групповым приводом в качестве электродвигателей могут быть использованы синхронный (рис. 5, а) или асинхронный (рис.5,б) электродвигатели. Некоторые характеристики электродвигателей, используемых для группового привода резиноперерабатывающих вальцев приведены ниже:
Количество вальцев 2 2—3 4 3—4
Мощность электродвигателя, кВт 217 276 376 372
Частота вращения, об/мин 150 94 94 150
|
|
Рис. 6. Кинематическая схема при вода одной секции вальцев:
1 — передний валок; 2—задний валок; 3 — трансмиссионный вал; 4 — подшипники трансмиссионного вала; 5— соединительные муфты; .6, 7 — малая и большая приводные шестерни; 8, 9 — передаточые шестерни [21].
При групповом приводе крутящий момент от электродвигателя передается по схеме рис. 1, б через редуктор, а по схеме рис.5, а — без редуктора через жесткую муфту 5 (рис. 6) на участок трансмиссионного вала, расположенного непосредственно под вальцами.
На рис. 6 изображена секция кинематической схемы привода одних вальцев от группового привода (см. рис. 5). Здесь передача крутящего момента осуществляется от трансмиссионного вала 3 к переднему и заднему валкам через ряд зубчатых передач. На трансмиссионный вал 3 насажена малая приводная шестерня 6, которая находится в зацеплении с большой приводной шестерней 7, сидящей на шейке заднего валка 2 вальцев. Далее крутящий момент от заднего валка передается на передний валок через фрикционные шестерни 8 и 9. Шестерни 8 и 9 насажены на шпонках соответственно на шейки заднего и переднего валков. По условиям работы вальцев эти шестерни должны допускать изменение межцентрового расстояния при изменении зазора между рабочими валками. С этой целью передаточные (фрикционные) прямозубые шестерни 8 и 9 имеют эвольвентное зубчатое зацепление с увеличенной высотой зубьев. Эвольвентное зубчатое зацепление допускает нормальную работу шестерен при изменении межцентрового расстояния. Изменение величины фрикции вальцев может быть достигнуто изменением количества зубьев фрикционных шестерен.
Вальцы могут быть сконструированы с левым и с правым расположением привода в зависимости от того, с какой стороны по отношению к рабочему месту у переднего валка расположена большая приводная шестерня 7 (рис. 6). Если она расположена с правой стороны от рабочего места, то вальцы имеют правый привод, если с левой стороны, — левый привод [11, 20-23]. Бывают случаи, когда при групповом приводе (при ремонте) необходимо средние вальцы отключить от привода; тогда малую приводную шестерню 6 выводят из зацепления с шестерней 7. Для уменьшения износа все шестерни (передаточные и приводные) вальцев изготавливаются, как правило, из качественной углеродистой стали [21].
Конспект лекций
по дисциплине «Процессы и аппараты химической технологии»
по направлению 240000 «Химическая и биотехнология»
специальности 240500 «Технология переработки пластических масс и эластомеров»
и специализации 240502 «Химия и технология переработки эластомеров»
для студентов специальности 240502 «Технология переработки пластических масс и эластомеров»
(заочная форма обучения)
Омск 2012
«Процессы и аппараты химической технологии»
Лекция №1
Техническая гидродинамика
В химической промышленности широко распространены процессы перемещения жидкостей, газов и паров, а также их хранения.
Техническая гидравлика является наукой о равновесии и движении жидкости (гидростатика, гидродинамика).
Гидродинамические закономерности в значительной степени определяют ход процессов теплопередачи, массопередачи и химических реакций в химических аппаратах.
Движение жидкостей и газов характеризуются одними и теми же законами, поэтому в гидравлике под жидкостью понимают как собственно жидкость, так и газы.
Под жидкостью понимают вещества, обладающие текучестью. Данные вещества не способны сохранять свою форму и полностью заполняют занимаемый ими объём.
Давление в жидкости и газе
Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности, называется давлением. За единицу давления принимается такое давление, которое производит сила в 1 Н, действующая на поверхность площадью 1 м2 перпендикулярно этой поверхности. Следовательно, чтобы определить давление, надо силу, действующую перпендикулярно поверхности, разделить на площадь поверхности.
Известно, что молекулы газа беспорядочно движутся. При своем движении они сталкиваются друг с другом, а также со стенками сосуда, в котором находится газ. Молекул в газе много, потому и число их ударов очень велико. Например: число ударов молекул воздуха, находящегося в комнате, на поверхность площадью 1 см2 за 1 с выражается двадцатитрехзначным числом. Хотя сила удара отдельной молекулы мала, но действие всех молекул о стенки сосуда значительно, оно и создает давление газа.
Итак, давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа.
При уменьшении объема газа его давление увеличивается, а при увеличении объема — уменьшается, если масса и температура газа остаются неизменными.
Давление, производимое на жидкость или газ, передается без изменения в каждую точку объема жидкости или газа (закон Паскаля).
На основе закона Паскаля легко объяснить следующий опыт.
Возмём полый шар, имеющий в различных местах узкие отверстия. К шару присоединена трубка, в которую вставлен поршень. Если набрать воды в шар и вдвинуть в трубку поршень, то вода польется из всех отверстий шара. В этом опыте поршень давит на поверхность воды в трубке. Частицы воды, находящиеся под поршнем, уплотняясь, передают его давление другим слоям, лежащим глубже. Таким образом, давление поршня передается в каждую точку жидкости, заполняющей шар, и часть воды выталкивается из шара в виде струек, вытекающих из всех отверстий.
Если шар заполнить дымом, то при вдвигании поршня в трубку из отверстий шара начнут выходить струйки дыма. Этот опыт подтверждает, что газ передает производимое на него давление во все стороны одинаково.
Опустим трубку с резиновым дном, в которую налита вода, в более широкий сосуд с водой. Мы увидим, что по мере опускания трубки резиновая пленка постепенно выпрямляется. Полное выпрямление пленки показывает, что силы, действующие на нее сверху и снизу, равны. Полное выпрямление пленки наступает тогда, когда уровни воды в трубке и сосуде совпадают.
Итак, опыт показывает, что внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям. С глубиной давление увеличивается. Газы в этом отношении не отличаются от жидкостей.
Мембранный манометр
Как измерить давление жидкости на поверхность твердого тела? Как измерить, например, давление воды на дно стакана? Дно стакана деформируется под действием сил давления. Зная величину деформации, мы могли бы определить величину вызвавшей ее силы и рассчитать давление, но эта деформация настолько мала, что измерить ее практически невозможно. Поскольку судить по деформации данного тела о давлении, оказываемом на него жидкостью, удобно лишь в том случае, когда деформация достаточно велика, то для практического определения давления жидкости пользуются специальными приборами — манометрами, в которых деформации имеют сравнительно большую, легко измеримую величину.
Простейший мембранный манометр устроен следующим образом. Тонкая упругая пластинка (мембрана) герметически закрывает пустую коробку. К мембране присоединен указатель, вращающийся около оси. При погружении прибора в жидкость мембрана прогибается под действием сил давления, ее прогиб передается в увеличенном виде указателю, передвигающемуся по шкале. Каждому положению указателя соответствует определенный прогиб мембраны, а, следовательно, и определенная сила давления на мембрану. Зная площадь мембраны, можно от сил давления перейти к самим давлениям. Можно непосредственно измерять давление, если заранее проградуировать манометр, т.е. определить, какому давлению соответствует то или иное положение указателя на шкале. Для этого нужно подвергнуть манометр действию давлений, величина которых известна, и, замечая положение стрелки указателя, проставить соответственные цифры на шкале прибора.
Воздушную оболочку, окружающую Землю, называют атмосферой (гр. atmos пар, воздух и sphaire шар).
Атмосфера, как показали наблюдения за полетом искусственных спутников Земли, простирается на высоту нескольких тысяч километров. Мы живем на дне огромного воздушного океана. Поверхность Земли — дно этого океана.
Вследствие действия силы тяжести верхние слои воздуха, подобно воде океана, сжимают нижние слои. Воздушный слой, прилегающий непосредственно к Земле, сжат больше всего и согласно закону Паскаля передает производимое на него давление по всем направлениям.
В результате этого земная поверхность и тела, находящиеся на ней, испытывают давление всей толщи воздуха, или атмосферное давление.
В практике для измерения атмосферного давления используют металлический барометр, называемый анероидом (гр. a…, an… — начальная часть слова со значением отрицания; neros влажный; eidos вид). Анероид — один из видов барометра, в котором изменения атмосферного давления определяются по деформации металлической коробки с сильным разрежением внутри.

Внешний вид анероида изображен на рисунке. Главная его часть — металлическая коробочка 1 с волнистой (гофрированной) поверхностью. Из этой коробочки выкачан воздух, а чтобы атмосферное давление не раздавило ее, крышку оттягивают вверх пружиной 2. При увеличении атмосферного давления крышка прогибается вниз и натягивает пружину. При уменьшении давления пружина выпрямляет крышку. К пружине с помощью передаточного механизма 3 прикреплена стрелка-указатель 4, которая передвигается вправо или влево при изменении давления. Под стрелкой укреплена шкала, деления которой нанесены по показаниям ртутного барометра. Так, число 750, против которого стоит стрелка анероида, показывает, что в данный момент в ртутном барометре высота ртутного столба 750 мм. Следовательно, атмосферное давление равно 750 мм рт. ст., или 1000 гПа.
Знание атмосферного давления весьма важно для определения погоды на ближайшие дни, так как изменение атмосферного давления связано с изменением погоды. Барометр — необходимый прибор при метеорологических наблюдениях.
Лекция №3
Нагнетательные технические устройства
1. Определение нагнетательных технических устройств, их виды.
Технические устройства, в которых происходит преобразование механической энергии в энергию движения жидкости или газа, называются нагнетательными.
Нагнетательные технические устройства (нагнетательные машины) делятся на:
- гидравлические (насосы);
- воздуходувные (компрессоры, вентиляторы).
Насосом называется гидравлическая машина (техническое устройство) для перемещения капельной жидкости за счет сообщаемой ей энергии.
Насос является основным элементом насосной установки, включающей в себя также:
- привод (электродвигатель, двигатель внутреннего сгорания);
- основание (фундамент), на который монтируется насос или двигатель.
В отдельных случаях основание может отсутствовать. Например, в современных системах отопления электронасос монтируется непосредственно на магистральном трубопроводе.
Насосы, в свою очередь, по принципу действия делятся на:
- объёмные,
- динамические.
Объёмные насосы действуют по принципу вытеснения жидкости в результате её сжатия (поршневые, роторные, диафрагменные).
Динамические насосы действуют по принципу силового воздействия на жидкость (на перемещаемую среду, жидкость или газ) (лопастные насосы, вихревые, струйные).
Лекция №4
Основы теплопередачи
Перенос теплоты
Решающую роль в восприятии окружающего мира играют характеристики, сохраняющиеся в замкнутых системах: масса, количество движения, момент количества движения, энергия и энтропия.
В учении о теплообмене рассматриваются процессы распространения теплоты в твердых, жидких и газообразных телах. Эти процессы по своей физико-механической природе весьма многообразны, отличаются большой сложностью и обычно развиваются в виде целого комплекса разнородных явлений.
Перенос теплоты может осуществляться тремя способами: теплопроводностью, конвекцией и излучением, или радиацией. Эти формы глубоко различны по своей природе и характеризуются различными законами.
Процесс переноса теплоты теплопроводностью происходит между непосредственно соприкасающимися телами или частицами тел с различной температурой. Учение о теплопроводности однородных и изотропных тел опирается на весьма прочный теоретический фундамент. Оно основано на простых количественных законах и располагает хорошо разработанным математическим аппаратом. Теплопроводность представляет собой молекулярный процесс передачи теплоты.
При определении переноса теплоты теплопроводностью в реальных телах встречаются известные трудности, которые на практике до сих пор удовлетворительно не решены. Эти трудности состоят в том, что тепловые процессы развиваются в неоднородной среде, свойства которой зависят от температуры и изменяются по объему; кроме того, трудности возникают с увеличением сложности конфигурации системы.
Уравнение теплопроводности имеет вид:
 ;
; 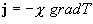 . (1)
. (1)
Оно выражает тот факт, что изменения теплосодержания определенной массы вещества, заключенного в единице объема, определяются различием между притоком и вытеканием энергии (дивергенцией плотности теплового потока j) при условии, что внутренних источников энергии нет. Тепловой поток пропорционален градиенту температуры и направлен в сторону ее падения; x — коэффициент теплопроводности.
При разработке методов исследования композиционных материалов весьма трудно и, по-видимому, не имеет смысла (в тех случаях, когда это можно практически реализовать) полностью учитывать структуру композита. В связи с этим возникла необходимость связать механику композитных материалов с механизмами элементов конструкций, развивающимися обычно в рамках континуальных процессов. Эта задача решается в процессе создания теории определения приведенных свойств композитных материалов различных структур (слоистые, волокнистые и др.) при описании их поведения в рамках континуальных представлений. Совершается переход от кусочно-однородной среды к однофазной.
Рассмотрим двухфазный композитный материал, представляющий собой матрицу, в которой случайным образом распределены включения второй фазы — армирующий элемент, имеющий приблизительно равноосную форму. Количество включений достаточно велико на участке изменения температуры. Пусть некая характеристика матрицы — А1, а включений — А2. Тогда можно представить композит как новый материал с промежуточными характеристиками между характеристиками матрицы и включений.
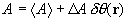 , (2)
, (2)
где 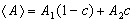 ,
, 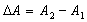 ,
, 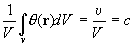 .
.
Подстановка (2) в (1) дает:
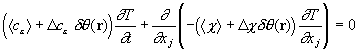 . (3)
. (3)
Имеем операторы:
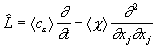 ; (4а)
; (4а)
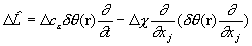 . (4б)
. (4б)
После преобразования Фурье получаем:
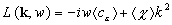 ;
;
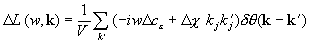 .
.
Уравнение для функции Грина:
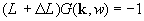 и
и 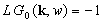 ,
,
где 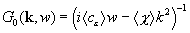 . (5)
. (5)
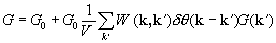 — уравнение Дайсона. (6)
— уравнение Дайсона. (6)
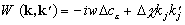 .
.
Функция Грина G0 описывает однородный материал со средними характеристиками, определяемыми по правилу смесей (2), а оператор W (k, k') можно назвать оператором возмущения, поскольку он определяет форму и расположение неоднородностей.
Решим уравнение итерациями:
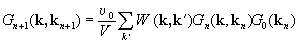 .
.
Вычислим сначала W2 (k, k2):
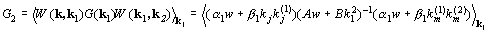 .
.
Здесь 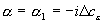 ,
, 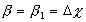 ,
, 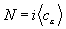 ,
, 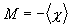 .
.
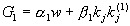 ;
;
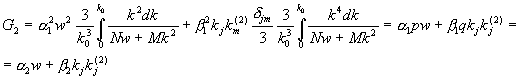 ;
;
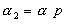 ,
, 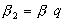 ,
, 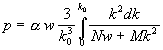 ,
, 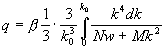 . (7)
. (7)
Теперь определим:
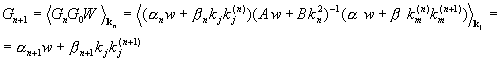 ;
;
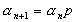 ,
, 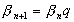 ,
, 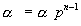 ,
, 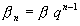 ,
, 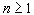 .
.
Теперь необходимо вычислить:
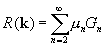 ;
;
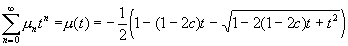 ;
;
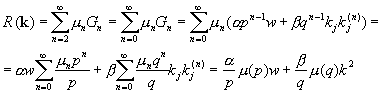 .
.
Таким образом,
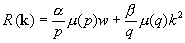 . (8)
. (8)
Подставляем в (6) равенство (8):
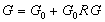 ;
;
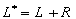 , где
, где 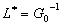 и
и 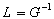 . (9)
. (9)
Подставляем (5) в (9):
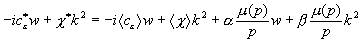 .
.
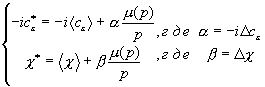 ;
;
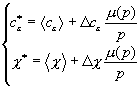 .
.
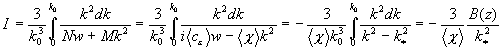 ,
,
где 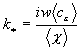 и
и 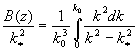 ;
;
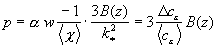 . (10)
. (10)
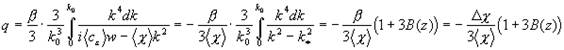 (11),
(11),
где 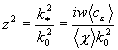 ;
; 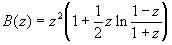 ; (12)
; (12)
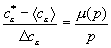 ;
;
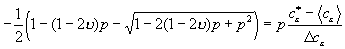 ;
;
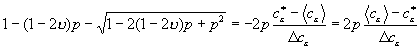 ;
;
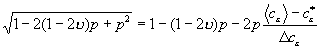
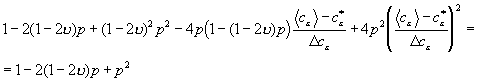 ;
;
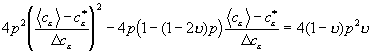 ;
;
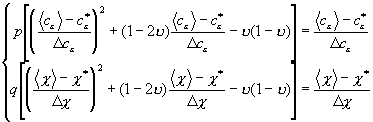 . (13)
. (13)
Ограничимся первым приближением:
` 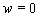 ,
,  ,
,  ,
,
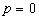 ,
, 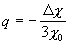 ,
, 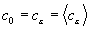 . (14)
. (14)
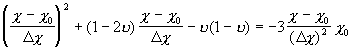 ;
;
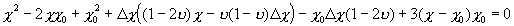 .
.
Рассмотрим:
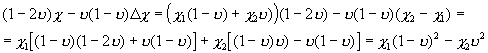 ;
;
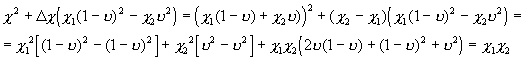 ;
;
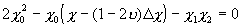 ;
;
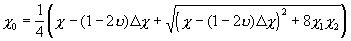 . (15)
. (15)
Ограничимся вторым приближением:
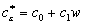 ,
, 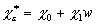 . (16)
. (16)
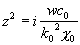 ,
, 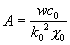 . (17)
. (17)
Из (12) найдем:
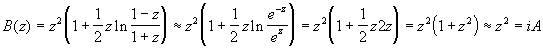 . (18)
. (18)
Подставляя (18) с учетом (16) в (10), получим:
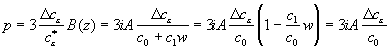 . (19)
. (19)
Теперь подставляем (19) с учетом (16) в (13), получим:
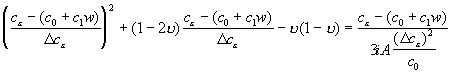 ;
;
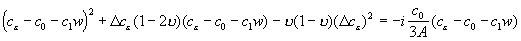 ;
;
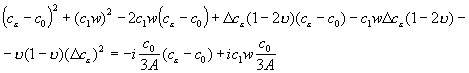 .
.
Коэффициентами при 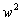 ,
, 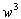 из-за малости произведения пренебрегаем, а коэффициенты без
из-за малости произведения пренебрегаем, а коэффициенты без 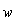 обращаются в 0 из-за (14):
обращаются в 0 из-за (14):
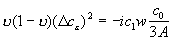 ,
,
подставляя (17), найдем:
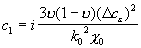 . (20)
. (20)
Подставляя (18) в (11) с учетом (16), получим:
Теперь подставляем (21) с учетом (16) в (13), получим:
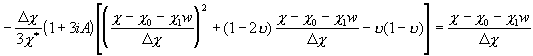
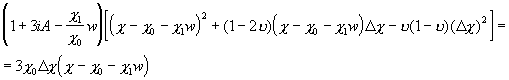 .
.
Коэффициентами при 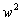 ,
, 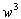 из-за малости произведения пренебрегаем, а коэффициенты без
из-за малости произведения пренебрегаем, а коэффициенты без 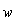 обращаются в 0 из-за (15):
обращаются в 0 из-за (15):
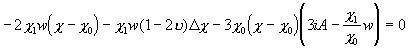 ;
;
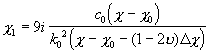 . (22)
. (22)
Ограничимся третьим приближением:
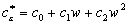 ,
, 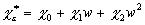 . (23)
. (23)
Подставляя (18) с учетом (23) в (10), получим:
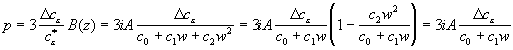 . (24)
. (24)
Теперь подставляем (24) с учетом (23) в (13), получим:
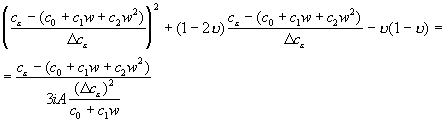 ;
;
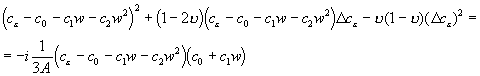 ;
;
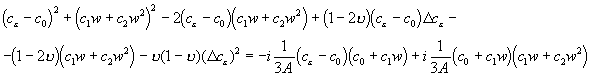 .
.
Коэффициентами при 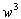 ,
, 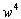 ,
, 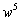 из-за малости произведения пренебрегаем, а коэффициенты без
из-за малости произведения пренебрегаем, а коэффициенты без 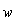 обращаются в 0 из-за (14), а с
обращаются в 0 из-за (14), а с 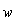 — из-за (18):
— из-за (18):
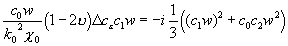 ;
;
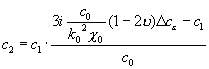 . (25)
. (25)
Подставляя (18) в (11) с учетом (23), получим:
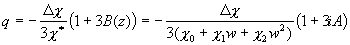 . (26)
. (26)
Теперь подставляем (26) с учетом (23) в (13), получим:
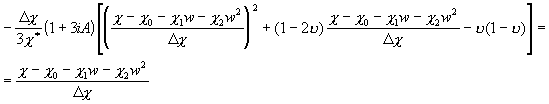 ;
;
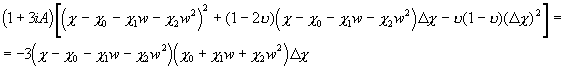 .
.
Коэффициентами при 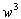 ,
, 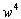 ,
, 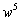 из-за малости произведения пренебрегаем, а коэффициенты без
из-за малости произведения пренебрегаем, а коэффициенты без 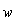 обращаются в 0 из-за (15), а с
обращаются в 0 из-за (15), а с 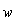 — из-за (22):
— из-за (22):
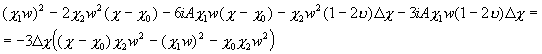 ;
;
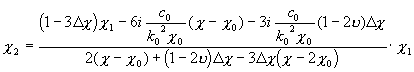 . (27)
. (27)
Анализ с1, с2, с3 и x0, x1, x2 показывает, что c0, c2 и x0, x2 — действительные коэффициенты, а c1, x1 — мнимые.
Физический смысл увеличения коэффициента теплоотдачи с увеличением скорости жидкости (газа).
Рассмотрим процесс теплоотдачи от потока теплоносителя к продольно омываемой им пластине. Скорость и температура набегающего потока постоянны и равны w ж и t ж (рис. 2.1).
Частицы жидкости, непосредственно соприкасающиеся с поверхностью, адсорбируются («прилипают») к ней. Соприкасаясь с неподвижным слоем, тормозятся и более удаленные от поверхности слои жидкости. Зона потока, в которой наблюдается уменьшение скорости (w<wж), вызванное вязким взаимодействием жидкости с поверхностью, называется гидродинамическим пограничным слоем. За пределами пограничного слоя течет невозмущенный поток. Четкой границы между ними нет, так как скорость w по мере удаления от поверхности постепенно (асимптотически) возрастает до wж. Практически за толщину гидродинамического пограничного слоя условно принимают расстояние от поверхности до точки, в которой скорость w отличается от скорости невозмущенного потока wж, незначительно (обычно на 1 %).
 На начальном участке (при малых значениях х) гидродинамический слой очень тонок (в лобовой точке с координатой х=0 толщина равна нулю) и течение в нем ламинарное — струйки жидкости движутся параллельно, не перемешиваясь. При удалении от лобовой точки толщина пограничного слоя растет. На некотором расстоянии х = хkp ламинарное течение становится неустойчивым. В пограничном слое появляются вихри (турбулентные пульсации скорости). Постепенно турбулентный режим течения распространяется почти на всю толщину гидродинамического пограничного слоя. Лишь около самой поверхности пластины в турбулентном пограничном слое сохраняется тонкий ламинарный, или вязкий, подслой, где скорость невелика и силы вязкости гасят турбулентные вихри.
На начальном участке (при малых значениях х) гидродинамический слой очень тонок (в лобовой точке с координатой х=0 толщина равна нулю) и течение в нем ламинарное — струйки жидкости движутся параллельно, не перемешиваясь. При удалении от лобовой точки толщина пограничного слоя растет. На некотором расстоянии х = хkp ламинарное течение становится неустойчивым. В пограничном слое появляются вихри (турбулентные пульсации скорости). Постепенно турбулентный режим течения распространяется почти на всю толщину гидродинамического пограничного слоя. Лишь около самой поверхности пластины в турбулентном пограничном слое сохраняется тонкий ламинарный, или вязкий, подслой, где скорость невелика и силы вязкости гасят турбулентные вихри.
Аналогичным образом осуществляется и тепловое взаимодействие потока с пластиной. Частицы жидкости, «прилипшие» к поверхности, имеют температуру, равную температуре поверхности t с. Соприкасающиеся с этими частицами движущиеся слои жидкости охлаждаются, отдавая им свою теплоту. От соприкосновения с этими слоями охлаждаются следующие более удаленные от поверхности слои потока — так формируется тепловой пограничный слой, в пределах которого температура меняется от tc на поверхности до t ж в невозмущенном потоке. По аналогии с гидродинамическим пограничным слоем толщина теплового пограничного слоя δт принимается равной расстоянию от поверхности до точки, в которой избыточная температура жидкости V = t — lc отличается от избыточной температуры невозмущенного потока V ж = t ж — lc на малую величину (обычно на 1 %).
С удалением от лобовой точки количество охлаждающейся у пластины жидкости увеличивается, и толщина теплового пограничного слоя возрастает аналогично возрастанию δт. В общем случае толщины теплового и гидродинамического слоев не равны, но часто достаточно близки друг к другу, особенно в газах.
При ламинарном течении тепловой поток от охлаждающейся в пограничном слое жидкости переносится к поверхности пластины только за счет теплопроводности. При этом плотность теплового потока по толщине пограничного слоя неодинакова: на внешней границе q =0, ибо дальше жидкость не охлаждается; по мере приближения к поверхности значение q возрастает. Для качественного анализа можно предположить, что плотность теплового потока q по всей толщине пограничного слоя такая же, как и у поверхности. Это условие соответствует задаче о переносе теплоты теплопроводностью через плоскую стенку (пограничный слой толщиной δт с температурами tc и tж на поверхностях).
С увеличением толщины теплового пограничного слоя при ламинарном течении жидкости у поверхности пластины интенсивность теплоотдачи уменьшается. В переходной зоне общая толщина пограничного слоя продолжает возрастать, однако значение α при этом увеличивается, потому что толщина ламинарного подслоя убывает, а в образующемся турбулентном слое тепло переносится не только теплопроводностью, но и конвекцией вместе с перемещающейся массой, т. е. более интенсивно. В результате суммарное термическое сопротивление теплоотдачи убывает.
После стабилизации толщины ламинарного подслоя в зоне развитого турбулентного режима коэффициент теплоотдачи вновь начинает убывать из-за возрастания общей толщины пограничного слоя.
При течении жидкости в трубе толщина пограничного слоя вначале растет симметрично по всему периметру, как на пластине (рис. 4.4а), до тех пор, пока слои с противоположных стенок не сольются на оси трубы. Дальше движение стабилизируется и фактически гидродинамический (аналогично и тепловой) пограничный слой заполняет все сечение трубы. В зависимости от конкретных условий пограничный слой на начальном участке может успеть перейти в турбулентный, а может и не успеть. Соответственно стабилизированный режим течения в трубе будет либо турбулентным с ламинарным подслоем около стенки, либо ламинарным по всему сечению.
В связи с особенностями течения жидкости в трубе изменяется и само понятие коэффициента теплоотдачи. Для пластины коэффициент а рассчитывался как отношение плотности теплового потока q к разности температур внешнего невозмущенного потока и поверхности (или наоборот при t с > t ж). В трубе пограничный слой занимает все сечение и невозмущенного потока нет, поэтому под коэффициентом теплоотдачи понимают отношение плотности теплового потока q к разности температуры стенки и среднемассовой температуры жидкости, протекающей через данное сечение трубы. Экспериментально среднемассовая температура жидкости определяется измерением ее температуры после хорошего перемешивания.
 Локальный коэффициент теплоотдачи от трубы к текущей в ней жидкости изменяется лишь на начальном участке (рис. 4.4б), а на участке стабилизированного течения αст = const, поскольку толщина пограничного слоя (δт= r) постоянна. С увеличением скорости течения теплоносителя в трубе αст возрастает из-за уменьшения толщины ламинарного подслоя, а с увеличением диаметра трубы уменьшается, поскольку растет толщина всего пограничного слоя δт= r .
Локальный коэффициент теплоотдачи от трубы к текущей в ней жидкости изменяется лишь на начальном участке (рис. 4.4б), а на участке стабилизированного течения αст = const, поскольку толщина пограничного слоя (δт= r) постоянна. С увеличением скорости течения теплоносителя в трубе αст возрастает из-за уменьшения толщины ламинарного подслоя, а с увеличением диаметра трубы уменьшается, поскольку растет толщина всего пограничного слоя δт= r .
Критерии подобия при подсчете величин коэффициентов теплоотдачи
При подсчете величин коэффициентов теплоотдачи применяются основные критерии подобия:
Критерий Прандтля:

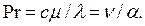
Критерий Рейнольдса:
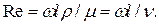
Критерий Галилея:
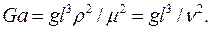
Критерий Грасгофа:
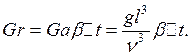
Критерий Пекле:
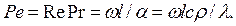
Дата: 2019-04-23, просмотров: 332.