(приложение к протоколу №)
Среднее арифметическое
 , 
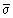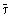
| Среднее квадратическое отклонение S | Односторонняя доверителями вероятность β(p) | Доверительный интервал ε | Вид закона распределения |
ПРИМЕРЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ИСПЫТАНИЙ
Количество образцов, необходимое для проведения эксперимента, определяют в соответствии с приложением 2.
По табл. 1 для δ = 10 % = 0,1; β = 0,95 и υ = 10 % = 0,1 в случае нормального закона распределения n = 5.
Пример 1
При обработке результатов испытаний пяти паяных образцов был получен следующий вариационный ряд значений σв 18,7, 18,2; 17,4; 16,2; 16,0 кгс/мм2.
Среднее арифметическое значение подсчитывают по формуле (12)
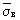= (18,7 + 18,2 + 17,4 + 16,2 + 16,0)/5 = 17,3 кгс/мм2.
Для определения среднего квадратического отклонения находят значение
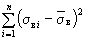(см. табл. 15).
Таблица 15
кгс/мм2
| i | σвi |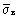 
| 
| 
| 
|
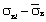
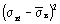
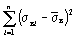
| 1 | 18,7 | 17,3 | +1,4 | 1,96 | 5,68 |
| 2 | 18,2 | +0,9 | 0,81 | ||
| 3 | 17,4 | +0,1 | 0,01 | ||
| 4 | 16,2 | -1,1 | 1,21 | ||
| 5 | 16,0 | -1,3 | 1,69 |
По формуле (14) определяют среднее квадратическое отклонение
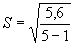= 1,19 кгс/мм2.
Границы доверительного интервала случайной погрешности вычисляют по формуле (19)
ε = 1,19·2,132/5 = 1,13 кгс/мм2.
Значение t находят по табл. 10 или 11. Для K = n - 1 = 4 при β = 0,95.
Проверяют коэффициент вариации, для чего по формуле (27) находят его значение υ = 1,19/17,3 = 0,0687, и результат сравнивают с принятым коэффициентом.
Полученный коэффициент вариации меньше заданного, следовательно n определено правильно.
Для оценки принадлежности резко выделяющегося (выпадающего) значения σв* данному вариационному ряду и принятия решения об исключении или оставлении σв* = σв1 = 18,7 кгс/мм2 в составе ряда определяют среднее квадратическое отклонение без выпадающего значения
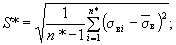(29)
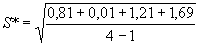= 1,11 кгс/мм2.
Находят отношение разности выпадающего значения и среднего арифметического к среднему квадратическому отклонению:
Un* = (σв* - 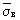)/S*; (30)
Un* = (18,7 - 17,3)/1,11 = 1,26.
Полученный результат сравнивают со h, взятым из табл. 16 или 17 для данного числа образцов n* и принятой доверительной вероятности β.
Таблица 16
Предельные значения h при n < 21
| Число образцов n* | Предельные значения h при вероятности β | |
| 0,90 | 0,95 | |
| 3 | 1,15 | 1,15 |
| 4 | 1,42 | 1,46 |
| 5 | 1,60 | 1,67 |
| 6 | 1,73 | 1,82 |
| 7 | 1,83 | 1,94 |
| 8 | 1,91 | 2,03 |
| 9 | 1,98 | 2,11 |
| 10 | 2,03 | 2,18 |
| 11 | 2,09 | 2,23 |
| 12 | 2,13 | 2,29 |
| 13 | 2,17 | 2,33 |
| 14 | 2,21 | 2,37 |
| 15 | 2,25 | 2,41 |
| 16 | 2,28 | 2,44 |
| 17 | 2,31 | 2,48 |
| 18 | 2,34 | 2,50 |
| 19 | 2,36 | 2,53 |
| 20 | 2,38 | 2,56 |
| n* = n - 1. | ||
| Примечание. Величины, помеченные звездочкой, принадлежат новому вариационному ряду без анормальных («выпадающих») значений. | ||
Если Un* ≥ h, то подозреваемый в анормальности результат может быть исключен, в противном случае он принадлежит данному вариационному ряду и его не исключают.
При n ≤ 21 значение h находят по табл. 16.
Таблица 17
Предельные значения h при n ≥ 21
| Число образцов n* | Предельные значения h при вероятности β | ||
| 0,90 | 0,95 | 0,99 | |
| 20 | 2,559 | 2,799 | 3,289 |
| 25 | 2,635 | 2,870 | 3,351 |
| 30 | 2,696 | 2,928 | 3,402 |
| 40 | 2,792 | 3,015 | 3,480 |
| 50 | 2,800 | 3,082 | 3,541 |
| 100 | 3,076 | 3,285 | 3,723 |
| 250 | 3,339 | 3,534 | 3,946 |
где n* = п - 1.
Из табл. 16 для n* = 4 и β = 0,95 находят h = 1,46, т.е.
Un* < h.
Значение σв, полученное при испытании первого образца, не является грубой погрешностью и принадлежит данному вариационному ряду.
Следовательно, значения, полученные при статистической обработке результатов испытаний, являются окончательными:
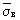= 17,3 кгс/мм2, S = 1,19 кгс/мм2; β = 0,95, ε = 1,13 кгс/мм2.
Пример 2
При обработке результатов испытаний пяти паяных образцов получен следующий вариационный ряд значений σв 18,7; 17,8; 17,1; 16,7; 16,2 кгс/мм2.
Среднее арифметическое значение 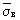= 17,3 кгс/мм2.
Таблица 18
| i | σвi |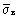
| 
|
| 
|
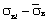
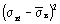
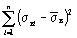
| 1 | 18,7 | 17,3 | +1,4 | 1,96 | 3,82 |
| 2 | 17,8 | +0,5 | 0,25 | ||
| 3 | 17,1 | -0,2 | 0,04 | ||
| 4 | 16,7 | -0,6 | 0,36 | ||
| 5 | 16,2 | 1,1 | 1,21 |
По формуле (14) определяют среднее квадратическое отклонение
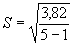= 0,977 кгс/мм2,
по формуле (19) находят
ε = 0,977·2,132/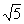 
= 0,93 кгс/мм2.
Определяют по формуле (27) расчетный коэффициент вариации
υ = 0,977/17,3 = 0,0565
υ расчетное меньше υ заданного, следовательно n определено правильно.
Определение анормального (выпадающего) результата в выборке
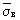= 17,3 кгс/мм2,
σв* = σв1 = 18,7 кгс/мм2,
для чего по формуле (14) подсчитывают S*, причем σв* = 18,7 кгс/мм2 в расчет не принимают
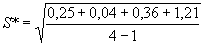= 0,787 кгс/мм2.
По формуле (30) находим
Un* = (18,7 - 17,3)/0,787 = 1,78.
При табличном значении h = 1,46,
Un* > h
следовательно, значение σв, полученное при испытании первого образца, является грубой погрешностью и может быть исключено из данного вариационного ряда. В этом случае вычисляют новые значения 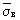, S и ε:
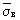= (17,8 + 17,1 + 16,7 + 16,2)/4 = 17 кгс/мм2;
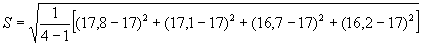= 0,68 кгс/мм2;
ε = 0,68·2,132/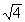 
= 0,72 кгс/мм2.
Записывают окончательный результат испытаний:
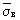= 17 кгс/мм2, S = 0,08 кгс/мм2, β = 0,95, T = 0,72 кгс/мма.
ИНФОРМАЦИОННЫЕ ДАННЫЕ
Дата: 2019-04-23, просмотров: 165.
