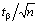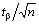1. Для статистической обработки результатов испытаний составляют вариационный ряд характеристик σ или τ.
Временное сопротивление при растяжении (σ), МПа (кгс/мм2), вычисляют по формуле
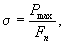 (10)
(10)
где Pmax - максимальная разрушающая нагрузка, Н (кгс);
Fn - площадь паяного шва, мм2.
Предел прочности на срез (τ), МПа (кгс/мм2), вычисляют по формуле
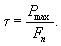 (11)
(11)
Далее проводят первичную статистическую обработку полученных значений σ и τ. За результат испытания принимают среднее арифметическое полученных характеристик  и
и 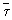 , среднее квадратическое отклонение S характеристик, границы доверительного интервала ε случайных погрешностей характеристик.
, среднее квадратическое отклонение S характеристик, границы доверительного интервала ε случайных погрешностей характеристик.
Вычисляют среднее арифметическое значение характеристик (  и
и 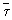 ) по формулам:
) по формулам:
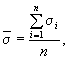 (12)
(12)
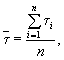 (13)
(13)
где σi - временное сопротивление при растяжении i-го образца, МПа;
τi - предел прочности на срез i-го образца, МПа;
n - число значений характеристик σ или τ в вариационном ряду;
i = 1, 2, 3 … n.
2. Среднее квадратическое отклонение характеристик определяют по формулам:
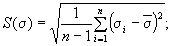 (14)
(14)
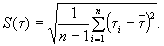 (15)
(15)
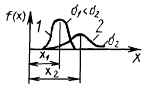
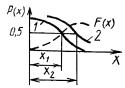
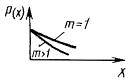
3. Для определения вида распределения результатов испытаний необходимо построить график распределения опытных данных в координатах вероятность - значение характеристики.
Затем сравнить его с известными законами распределения, приведенными в табл. 9.
Далее проверяют согласие распределения опытных данных с предполагаемым теоретическим распределением по критериям согласия.
4. Наиболее часто применяемым законом распределения является нормальный.
Формулы для расчета результатов испытаний:
при равноточных измерениях
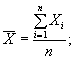 (16)
(16)
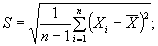 (17)
(17)
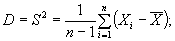 (18)
(18)
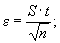 (19)
(19)
при неравноточных измерениях
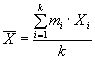 - среднее взвешенное; (20)
- среднее взвешенное; (20)
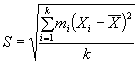 - взвешенное среднее квадратическое отклонение, (21)
- взвешенное среднее квадратическое отклонение, (21)
где n - число результатов испытаний;
mi - частота появления случайного значения в интервале;
Xi - значение переменной величины;
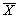 - среднее арифметическое;
- среднее арифметическое;
K - число интервалов;
S - среднее квадратическое;
D - дисперсия;
ε - границы доверительного интервала случайной погрешности;
t - коэффициент распределения Стьюдента, определяемый по табл. 10 и 11.
5. Определение несмещенной оценки среднего квадратического отклонения
S1 = Mk·S. (22)
Таблица 9
| Законы распределения | (х) | P(x) |
Нормальный (Гаусса)
 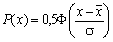
| 
| 
|
Логарифмически нормальный
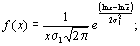 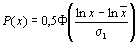
| 
| 
|
Экспоненциальный
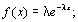 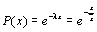
| 
| 
|
Вейбулла
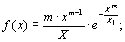 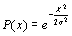
| 
| 
|
Рэлея
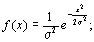 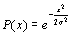
| 
| 
|
Гамма-распределение
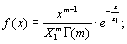 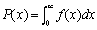
| 
| 
|
Равномерное распределение
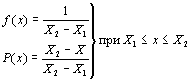
| 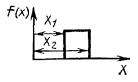
| 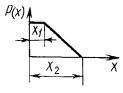
|
Таблица 10
Значение коэффициента Стьюдента t при односторонней доверительной вероятности β
| K | β | K | β | ||||
| 0,90 | 0,95 | 0,99 | 0,90 | 0,95 | 0,99 | ||
| t | t | ||||||
| 1 | 3,073 | 6,314 | 31,820 | 28 | 1,313 | 1,701 | 2,467 |
| 2 | 1,886 | 2,920 | 6,965 | 29 | 1,311 | 1,699 | 2,462 |
| 3 | 1,638 | 2,353 | 4,541 | 30 | 1,310 | 1,697 | 2,457 |
| 4 | 1,533 | 2,132 | 3,747 | 32 | 1,309 | 1,694 | 2,449 |
| 5 | 1,476 | 2,015 | 3,365 | 34 | 1,307 | 1,691 | 2,441 |
| 6 | 1,440 | 1,943 | 3,143 | 36 | 1,305 | 1,688 | 2,434 |
| 7 | 1,415 | 1,895 | 2,998 | 38 | 1,304 | 1,686 | 2,429 |
| 8 | 1,397 | 1,859 | 2,896 | 40 | 1,303 | 1,684 | 2,423 |
| 9 | 1,383 | 1,833 | 2,821 | 42 | 1,302 | 1,682 | 2,418 |
| 10 | 1,372 | 1,812 | 2,764 | 44 | 1,301 | 1,680 | 2,414 |
| 11 | 1,363 | 1,796 | 2,718 | 46 | 1,300 | 1,679 | 2,410 |
| 12 | 1,356 | 1,782 | 2,681 | 48 | 1,299 | 1,677 | 2,407 |
| 13 | 1,350 | 1,771 | 2,650 | 50 | 1,298 | 1,676 | 2,403 |
| 14 | 1,345 | 1,761 | 2,624 | 55 | 1,297 | 1,673 | 2,396 |
| 15 | 1,341 | 1,753 | 2,602 | 60 | 1,296 | 1,671 | 2,390 |
| 16 | 1,337 | 1,746 | 2,583 | 65 | 1,295 | 1,669 | 2,385 |
| 17 | 1,333 | 1,740 | 2,567 | 70 | 1,294 | 1,667 | 2,381 |
| 18 | 1,330 | 1,734 | 2,552 | 80 | 1,292 | 1,664 | 2,374 |
| 19 | 1,328 | 1,729 | 2,539 | 90 | 1,291 | 1,662 | 2,368 |
| 20 | 1,325 | 1,725 | 2,528 | 100 | 1,290 | 1,660 | 2,364 |
| 21 | 1,323 | 1,721 | 2,518 | 120 | 1,289 | 1,658 | 2,358 |
| 22 | 1,321 | 1,717 | 2,508 | 150 | 1,287 | 1,655 | 2,351 |
| 23 | 1,319 | 1,714 | 2,500 | 200 | 1,286 | 1,653 | 2,345 |
| 24 | 1,318 | 1,711 | 2,492 | 250 | 1,285 | 1,651 | 2,341 |
| 25 | 1,316 | 1,708 | 2,485 | 300 | 1,284 | 1,650 | 2,339 |
| 26 | 1,315 | 1,706 | 2,479 | 400 | 1,284 | 1,649 | 2,336 |
| 27 | 1,314 | 1,703 | 2,473 | 500 | 1,283 | 1,648 | 2,334 |
| ∞ | 1,282 | 1,645 | 2,326 | ||||
| K - число степеней свободы, K = n - 1 | |||||||
Таблица 11
Значение коэффициентов Стьюдента при двусторонней доверительной вероятности P
| K | P | ||||
| 0,90 | 0,95 | 0,98 | 0,99 | 0,999 | |
| t | |||||
| 4 | 2,132 | 2,776 | 3,747 | 4,604 | 8,610 |
| 5 | 2,015 | 2,571 | 3,365 | 4,032 | 6,859 |
| 6 | 1,943 | 2,447 | 3,143 | 3,707 | 5,959 |
| 7 | 1,895 | 2,365 | 2,998 | 3,499 | 5,405 |
| 8 | 1,860 | 2,306 | 2,896 | 3,355 | 5,041 |
| 9 | 1,833 | 2,262 | 2,821 | 3,250 | 4,781 |
| 10 | 1,812 | 2,228 | 2,764 | 3,169 | 4,587 |
| 11 | 1,796 | 2,201 | 2,718 | 3,106 | 4,437 |
| 12 | 1,782 | 2,179 | 2,681 | 3,055 | 4,318 |
| 13 | 1,771 | 2,160 | 2,650 | 3,012 | 4,221 |
| 14 | 1,761 | 2,145 | 2,624 | 2,977 | 4,140 |
| 15 | 1,753 | 2,131 | 2,602 | 2,947 | 4,073 |
| 16 | 1,746 | 2,120 | 2,583 | 2,921 | 4,015 |
| 18 | 1,734 | 2,103 | 2,552 | 2,878 | 3,922 |
| 20 | 1,725 | 2,086 | 2,528 | 2,845 | 3,850 |
| 25 | 1,708 | 2,060 | 2,485 | 2,787 | 3,725 |
| 30 | 1,697 | 2,042 | 2,457 | 2,750 | 3,646 |
| 35 | 1,689 | 2,030 | 2,437 | 2,724 | 3,591 |
| 40 | 1,684 | 2,021 | 2,423 | 2,704 | 3,551 |
| 45 | 1,679 | 2,014 | 2,412 | 2,689 | 3,522 |
| 50 | 1,676 | 2,008 | 2,403 | 2,677 | 3,497 |
| 60 | 1,671 | 2,000 | 2,390 | 2,660 | 3,460 |
| 70 | 1,667 | 1,995 | 2,381 | 2,648 | 3,436 |
| 80 | 1,664 | 1,990 | 2,374 | 2,639 | 3,416 |
| 90 | 1,662 | 1,987 | 2,368 | 2,632 | 3,401 |
| 100 | 1,660 | 1,984 | 2,364 | 2,626 | 3,391 |
| ∞ | 1,645 | 1,960 | 2,326 | 2,576 | 3,291 |
Таблица 12
Значения коэффициента Mk при K
| K | Mk | K | Mk | K | Mk | K | Mk |
| 1 | 1,253 | 8 | 1,032 | 15 | 1,017 | 30 | 1,008 |
| 2 | 1,128 | 9 | 1,028 | 16 | 1,016 | 35 | 1,007 |
| 3 | 1,085 | 10 | 1,025 | 17 | 1,015 | 40 | 1,006 |
| 4 | 1,064 | 11 | 1,023 | 18 | 1,014 | 45 | 1,006 |
| 5 | 1,051 | 12 | 1,021 | 19 | 1,013 | 50 | 1,005 |
| 6 | 1,042 | 13 | 1,019 | 20 | 1,013 | 60 | 1,004 |
| 7 | 1,036 | 14 | 1,018 | 25 | 1,010 | ||
| K = n - 1 - число степеней свободы. | |||||||
Границы доверительного интервала случайной погрешности при нормальном распределении находят по формуле
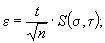 (23)
(23)
определение доверительных границ среднего квадратического отклонения
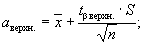 (24)
(24)
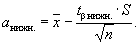 (25)
(25)
Значение 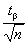 определяют по табл. 13.
определяют по табл. 13.
6. Дисперсия, полученная при неравноточных измерениях (расчет S2 - по интервалам на основе их середин), завышена. Для уточнения дисперсии применяется поправка Шеппарда.
S2 - с поправкой = S2 по интервалам + c2/12, (26)
где с - размер интервалов.
7. Далее следует провести проверку принадлежности характеристик σ или τ вариационного ряда к нормальному распределению.
8. Определяют расчетный коэффициент вариации и сравнивают его с принятым значением υ.
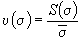 (27)
(27)
или 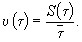 (28)
(28)
Если расчетный коэффициент вариации больше принятого, - объем испытаний пересчитывают для найденного коэффициента вариации.
Таблица 13
| n | β | n | β | ||||||
| 0,80 | 0,90 | 0,95 | 0,99 | 0,80 | 0,90 | 0,95 | 0,99 | ||
|
|
| ||||||||
| 2 | 0,973 | 2,180 | 4,460 | 22,500 | 25 | 0,171 | 0,264 | 0,342 | 0,498 |
| 3 | 0,613 | 1,080 | 1,690 | 4,020 | 27 | 0,164 | 0,253 | 0,328 | 0,477 |
| 4 | 0,489 | 0,819 | 1,180 | 2,270 | 29 | 0,159 | 0,244 | 0,316 | 0,458 |
| 5 | 0,421 | 0,685 | 0,953 | 1,670 | 31 | 0,153 | 0,235 | 0,304 | 0,441 |
| 6 | 0,375 | 0,602 | 0,823 | 1,370 | 33 | 0,149 | 0,228 | 0,295 | 0,425 |
| 7 | 0,342 | 0,544 | 0,734 | 1,190 | 35 | 0,144 | 0,221 | 0,280 | 0,413 |
| 8 | 0,317 | 0,500 | 0,670 | 1,060 | 37 | 0,140 | 0,214 | 0,278 | 0,400 |
| 9 | 0,296 | 0,466 | 0,620 | 0,966 | 39 | 0,136 | 0,209 | 0,270 | 0,389 |
| 10 | 0,279 | 0,437 | 0,580 | 0,892 | 41 | 0,133 | 0,203 | 0,263 | 0,378 |
| 11 | 0,265 | 0,414 | 0,546 | 0,833 | 43 | 0,130 | 0,198 | 0,256 | 0,369 |
| 13 | 0,242 | 0,393 | 0,494 | 0,744 | 45 | 0,127 | 0,194 | 0,250 | 0,360 |
| 15 | 0,224 | 0,347 | 0,455 | 0,678 | 47 | 0,124 | 0,190 | 0,245 | 0,392 |
| 17 | 0,210 | 0,324 | 0,423 | 0,627 | 49 | 0,121 | 0,186 | 0,240 | 0,344 |
| 19 | 0,198 | 0,305 | 0,398 | 0,586 | 51 | 0,119 | 0,182 | 0,235 | 0,337 |
| 21 | 0,188 | 0,288 | 0,376 | 0,552 | 56 | 0,114 | 0,173 | 0,224 | 0,320 |
| 23 | 0,178 | 0,275 | 0,358 | 0,523 | 61 | 0,109 | 0,166 | 0,214 | 0,306 |
9. В случае, если в вариационном ряду характеристик σ или τ, подчиняющемуся нормальному закону распределения, одно или несколько значений вызывают сомнение в принадлежности их к данному ряду, то используют правила оценки анормальности результатов испытаний для неприятия резко выделяющихся (выпадающих) значений.
Примечание. Если анормальное значение, характеризующее нижнюю границу свойства паяного соединения и являющееся минимальным, повторяется, а по фрактографическому анализу соединение качественное, то такой результат исключать не следует, а испытания необходимо повторить на увеличенной вдвое партии образцов.
10. При определении грубых погрешностей для других законов распределения применяют другие критерии для неприятия выпадающих значений. Использованный критерий должен быть указан в протоколе испытания.
11. При исключении одного или нескольких значений характеристик σ или τ из вариационного ряда следует пересчитать среднее арифметическое результатов измерений, среднее квадратическое отклонение и доверительные границы случайной погрешности для значений нового ряда.
12. Полученные значения являются окончательными результатами проведенных испытаний и оформляются в форме табл. 14, прилагаемой к протоколу испытаний.
Таблица 14
Дата: 2019-04-23, просмотров: 289.