Определитель матрицы А равен сумме произведений всех элементов некоторого столбца (строки) на их алгебраические дополнения:

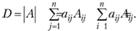
Рассмотрим примеры вычисления определителей (предполагается знание правил вычисления определителей второго порядка).

1. Вычислить определитель

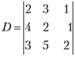
Разложим определитель D по элементам второго столбца: 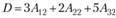. Переходя к минорам, имеем

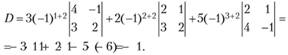
2. Вычислить определитель четвертого порядка

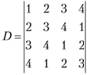
Используя свойства определителей, получим единичную первую строку и разложим по ней определитель D, аналогично поступим с первым столбцом преобразованного определителя:

Решение систем линейных уравнений

Рассмотрим систему из п линейных уравнений с п неизвестными (такие системы линейных уравнений называются определенными):

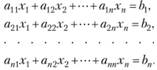(2.15)

Определитель А, составленный из коэффициентов при неизвестных, называют определителем системы (2.15):

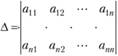
Решить систему уравнений (2.15) можно различными методами, в частности методом Крамера. В основе решения системы уравнений (2.15) методом Крамера лежит следующая теорема.

Теорема Крамера

Если определитель Δ системы (2.15) отличен от нуля, то система совместна и имеет единственное решение, которое можно найти по формуле

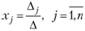
В этой формуле Δ_j является определителем, полученным из определителя системы Δ путем замены столбца j столбцом свободных членов.

Систему п линейных уравнений с п неизвестными (2.15) можно записать в матричном виде: АХ = В, где А - квадратная матрица порядка п, составленная из коэффициентов при неизвестных; X - вектор-столбец из неизвестных; В - вектор-столбец свободных членов:

Если А - невырожденная матрица, т.е. ее определитель 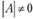, то можно определить A^-1. С учетом этого имеют место матричные соотношения:

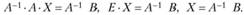(2.16)

Обратная матрица может быть определена на базе следующей теоремы.

Теорема 2.1. Если определитель матрицы А не равен нулю, то матрица А имеет обратную матрицу A^-1, которая находится по формуле

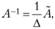
где 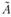- матрица, присоединенная к матрице А.

Матрица А составляется из алгебраических дополнений к элементам транспонированной матрицы:

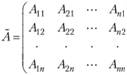
Таким образом, соотношение (2.16) лежит в основе решения системы уравнений (2.15) методом обратной матрицы (функция = МУМНОЖ (МОБР(А), В) Мастера функций MS Excel).

Рассмотрим систему т линейных уравнений с п неизвестными (при т < п такие системы называются неопределенными):

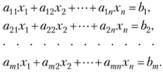(2.17)

или в векторной записи:

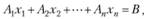
где

соответствующие вектор-столбцы.

Запишем расширенную матрицу этой системы в виде

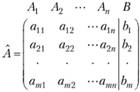
Элементарными преобразованиями системы (2.17) (или матрицы 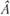) называются следующие преобразования:

o перестановка любых двух уравнений;

o умножение обеих частей одного из уравнений на любое отличное от нуля число;

o прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число, отличное от нуля;

o вычеркивание нулевой строки (уравнения с нулевыми коэффициентами и свободными членом, равным 0).

Можно показать, что элементарные преобразования переводят данную систему уравнений в эквивалентную систему. Две системы линейных уравнений называются эквивалентными, или равносильными, если каждое решение первой системы (если они существуют) является решением второй, и наоборот. Соответствующие расширенные матрицы также называются эквивалентными.

При практическом решении системы линейных уравнений методом Жордана - Гаусса последовательно над строками матрицы 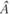выполняют элементарные преобразования, так что некоторое неизвестное исключается из всех уравнений, кроме одного, т.е. в составе расширенной матрицы формируется единичная подматрица.

В процессе решения могут встретиться следующие случаи.

1. Будет получена матрица 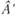, эквивалентная матрице 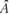, в левой части некоторой строки ее стоят нули, а в правой - число, отличное от нуля, что соответствует уравнению

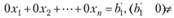
Это признак несовместности системы (2.17), т.е. система не имеет решений.

2. В результате преобразований получилась матрица А' вида

В этом случае система (2.17) совместна, определенная и имеет единственное решение: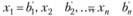

3. На некотором этапе получилась расширенная матрица вида

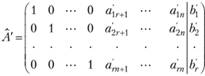
Система совместна и имеет бесчисленное множество решений. Общее решение системы можно записать в виде

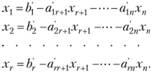
Придавая каждой из стоящих в правых частях равенств переменных 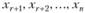произвольные значения, будем получать частные решения системы.

Неизвестные 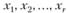называются базисными, или основными, они соответствуют линейно-независимым векторам

Таким образом, любые r переменных называются базисными (основными), если определитель матрицы коэффициентов при них отличен от нуля, а остальные (п - r) переменных называются свободными, или неосновными. Базисным решением системы уравнений называется частное решение, в котором неосновные переменные имеют нулевые значения. Каждому разбиению на основные и неосновные переменные соответствует одно базисное решение, а количество способов разбиения не превышает величины

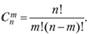
Если все компоненты базисного решения неотрицательны, то такое решение называется опорным.

Пример 2.3. Исследовать систему уравнений методом Жордана - Гаусса.

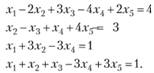
Решение. Запишем расширенную матрицу системы уравнений и последовательно преобразуем ее элементарными преобразованиями

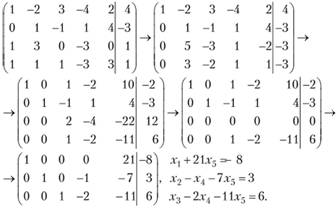
Таким образом, система совместна, имеет бесчисленное множество решений. Общее решение записывается в виде

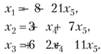
Любое частное решение получается из общего путем придания конкретных значений свободным переменным х₄ и х₅. Например, (-8; 4; 8; 1; 0) - частное решение. Одно из базисных решений получаем при х₄ = 0 и х₅ = 0 , т.е. (-8; 3; 6; 0; 0).

Число базисных решений не превосходит 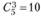. Перейдем к другому базисному решению, взяв в расширенной матрице в качестве базисных решений векторы А_иА₂ ,А₄ ; при этом переменные x_t,x₂ ,x₄ будут базисными, а х₃ ,х₅ - свободными. Переход от одного базиса к другому осуществим методом Жордана - Гаусса, т.е. используя элементарные преобразования:

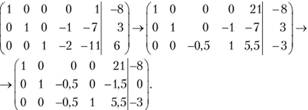
Таким образом, получено еще одно базисное решение: (-8; 0; 0; -3; 0) и т.д.

Заметим, что оба полученных базисных решения не являются опорными решениями; последнее решение является также вырожденным (базисная переменная х равна 0).