Математический аппарат линейного программирования
Изучение и понимание современных экономико-математических методов предполагает достаточно серьезную математическую подготовку экономистов. Для освоения задач и методов в пределах данной главы необходимы знания основных понятий и элементов высшей математики, матричной и векторной алгебры. Некоторые необходимые сведения из этих разделов математики приведены ниже.
Матрицы и определители
Рассмотрим т x п действительных чисел, записанных в виде прямоугольной таблицы из т строк и п столбцов:
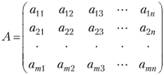
Данная таблица чисел называется числовой матрицей (в дальнейшем - просто матрицей). Числа аij, которые входят в матрицу, называются ее элементами. Индексы i и j элемента aij указывают соответственно номера строки и столбца, в которых расположен элемент aij. Матрицу, содержащую одну строку (или один столбец), называют также вектор-строкой (или вектор-столбцом).
Матрица, все элементы которой равны нулю, называется нулевой. Две матрицы называются равными, если числа строк и столбцов одной из них равны соответственно числам строк и столбцов другой и элементы этих матриц, расположенные на соответствующих местах, равны.
Матрицей, транспонированной к матрице А, называется матрица вида
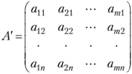
т.е. строками матрицы А являются столбцы, а столбцами - строки матрицы А.
Если число строк равно числу столбцов (т = n), матрицу называют квадратной матрицей порядка п.
Элементы а11, а22, a33, аnn, образуют так называемую главную диагональ квадратной матрицы; элементы a1n, а2n-1, ..., аn1 - побочную диагональ квадратной матрицы.
Рассмотрим некоторые действия над матрицами.
1. Произведением матрицы А на число λ (или, что то же самое, числа λ на матрицу А) называется матрица
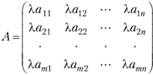
получающаяся из А путем умножения каждого ее элемента на число λ.
2. Под суммой двух матриц
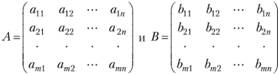
элементы которой равны суммам соответствующих элементов матриц А и В. При этом подразумевается, что число строк (столбцов) матрицы А равно числу строк (столбцов) матрицы В. Подобным же образом определяется и разность (А - В) матриц А и В.
Линейные операции над матрицами подчиняются обычным законам арифметики, например:
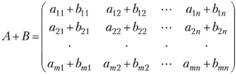
понимается матрица
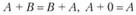
(все элементы матрицы 0 - нули),
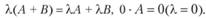
3. Произведением матрицы А из т строк и п столбцов на матрицу В из п строк и k столбцов называется матрица С = АВ, имеющая т строк и k столбцов, элемент Сij которой, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-гo столбца матрицы В, т.е. находится по формуле скалярного произведения i-й вектор-строки матрицы А на j-й вектор-столбец матрицы В:
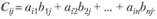
В случае квадратных матриц можно составить как произведение АВ, так и произведение ВА. В общем случае АВ≠ВА, т.е. переместительный закон для матриц не выполняется.
Для произведения матриц остаются в силе следующие законы арифметики.
1. Распределительный закон (А + В)С = АС + ВС, С(А + В) = СА + СВ.
2. Сочетательный закон (АВ)С = А(ВС).
Среди квадратных матриц особую роль играет матрица

все элементы которой, расположенные на главной диагонали, равны единице, а остальные - нулю. Можно проверить, что для любой матрицы А:
АЕ = ЕА = А. Матрица Е называется единичной.
Матрица В называется обратной для матрицы А, если АВ = ВА = Е. Матрица В, обратная матрице А, обозначается через A-1 (функция = МОБР() Мастера функций MS Excel).
С каждой квадратной матрицей определенным образом связано некоторое число, называемое ее определителем (функция =МОПРЕД() Мастера функций MS Excel).
Для вычисления определителя любого порядка необходимо знание его свойств и теоремы о разложении определителя.
Приведем основные свойства определителей.
1. При транспонировании матрицы ее определитель не меняется. Это свойство свидетельствует о полном равноправии строк и столбцов определителя. Следовательно, если некоторое утверждение справедливо относительно столбцов определителя, то аналогичное утверждение справедливо и для его строк.
2. Если все элементы какого-либо столбца (строки) определителя равны нулю, то и сам определитель равен нулю.
3. При перестановке двух любых столбцов (строк) определителя его знак меняется на противоположный, а абсолютная величина остается неизменной.
4. Определитель с двумя одинаковыми столбцами (строками) равен нулю.
5. Если j-й столбец (строка) Aj определителя D является линейной комбинацией
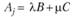
двух произвольных столбцов (строк) В и С, то и сам определитель оказывается линейной комбинацией
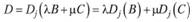
определителей Dj(B) и Dj(C).
Здесь Dj(B) и Dj(С) - определитель D, в котором столбец (строка) у заменен соответственно на столбец (строку) В и С. Остальные столбцы (строки) сохранены без изменения.
6. При умножении любого столбца (строки) определителя на произвольное число λ сам определитель умножается на это же число.
7. Если какой-либо столбец (строка) определителя является линейной комбинацией других его столбцов (строк), то определитель равен нулю.
8. Определитель не изменится, если к элементам любого его столбца (строки) прибавить соответствующие элементы другого столбца (строки), предварительно умноженные на одно и то же число.
Рассмотрим определитель n-го порядка:
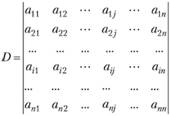
Выделим в нем некоторый элемент, например aij. Вычеркнем в определителе i-ю строку и j-й столбец, в которых расположен выделенный элемент аij. В результате останется определитель (n-1)-го порядка. Этот оставшийся определитель называется минором элемента аij в определителе D и обозначается Мij.
Величину 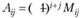 называют алгебраическим дополнением элемента aij в определителе D (или в соответствующей квадратной матрице).
называют алгебраическим дополнением элемента aij в определителе D (или в соответствующей квадратной матрице).
Теорема Крамера
Если определитель Δ системы (2.15) отличен от нуля, то система совместна и имеет единственное решение, которое можно найти по формуле
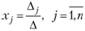
В этой формуле Δj является определителем, полученным из определителя системы Δ путем замены столбца j столбцом свободных членов.
Систему п линейных уравнений с п неизвестными (2.15) можно записать в матричном виде: АХ = В, где А - квадратная матрица порядка п, составленная из коэффициентов при неизвестных; X - вектор-столбец из неизвестных; В - вектор-столбец свободных членов:

Если А - невырожденная матрица, т.е. ее определитель 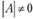 , то можно определить A-1. С учетом этого имеют место матричные соотношения:
, то можно определить A-1. С учетом этого имеют место матричные соотношения:
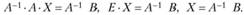 (2.16)
(2.16)
Обратная матрица может быть определена на базе следующей теоремы.
Теорема 2.1. Если определитель матрицы А не равен нулю, то матрица А имеет обратную матрицу A-1, которая находится по формуле
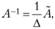
где 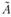 - матрица, присоединенная к матрице А.
- матрица, присоединенная к матрице А.
Матрица А составляется из алгебраических дополнений к элементам транспонированной матрицы:
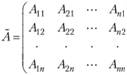
Таким образом, соотношение (2.16) лежит в основе решения системы уравнений (2.15) методом обратной матрицы (функция = МУМНОЖ (МОБР(А), В) Мастера функций MS Excel).
Рассмотрим систему т линейных уравнений с п неизвестными (при т < п такие системы называются неопределенными):
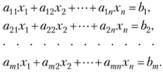 (2.17)
(2.17)
или в векторной записи:
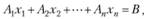
где 
соответствующие вектор-столбцы.
Запишем расширенную матрицу этой системы в виде
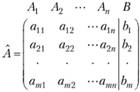
Элементарными преобразованиями системы (2.17) (или матрицы 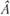 ) называются следующие преобразования:
) называются следующие преобразования:
o перестановка любых двух уравнений;
o умножение обеих частей одного из уравнений на любое отличное от нуля число;
o прибавление к обеим частям одного уравнения соответствующих частей другого, умноженных на любое число, отличное от нуля;
o вычеркивание нулевой строки (уравнения с нулевыми коэффициентами и свободными членом, равным 0).
Можно показать, что элементарные преобразования переводят данную систему уравнений в эквивалентную систему. Две системы линейных уравнений называются эквивалентными, или равносильными, если каждое решение первой системы (если они существуют) является решением второй, и наоборот. Соответствующие расширенные матрицы также называются эквивалентными.
При практическом решении системы линейных уравнений методом Жордана - Гаусса последовательно над строками матрицы 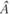 выполняют элементарные преобразования, так что некоторое неизвестное исключается из всех уравнений, кроме одного, т.е. в составе расширенной матрицы формируется единичная подматрица.
выполняют элементарные преобразования, так что некоторое неизвестное исключается из всех уравнений, кроме одного, т.е. в составе расширенной матрицы формируется единичная подматрица.
В процессе решения могут встретиться следующие случаи.
1. Будет получена матрица 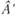 , эквивалентная матрице
, эквивалентная матрице 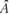 , в левой части некоторой строки ее стоят нули, а в правой - число, отличное от нуля, что соответствует уравнению
, в левой части некоторой строки ее стоят нули, а в правой - число, отличное от нуля, что соответствует уравнению
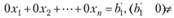
Это признак несовместности системы (2.17), т.е. система не имеет решений.
2. В результате преобразований получилась матрица А' вида

В этом случае система (2.17) совместна, определенная и имеет единственное решение: 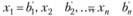
3. На некотором этапе получилась расширенная матрица вида
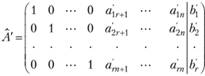
Система совместна и имеет бесчисленное множество решений. Общее решение системы можно записать в виде
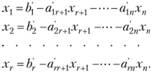
Придавая каждой из стоящих в правых частях равенств переменных 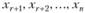 произвольные значения, будем получать частные решения системы.
произвольные значения, будем получать частные решения системы.
Неизвестные 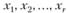 называются базисными, или основными, они соответствуют линейно-независимым векторам
называются базисными, или основными, они соответствуют линейно-независимым векторам 
Таким образом, любые r переменных называются базисными (основными), если определитель матрицы коэффициентов при них отличен от нуля, а остальные (п - r) переменных называются свободными, или неосновными. Базисным решением системы уравнений называется частное решение, в котором неосновные переменные имеют нулевые значения. Каждому разбиению на основные и неосновные переменные соответствует одно базисное решение, а количество способов разбиения не превышает величины
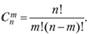
Если все компоненты базисного решения неотрицательны, то такое решение называется опорным.
Пример 2.3. Исследовать систему уравнений методом Жордана - Гаусса.
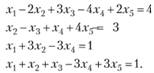
Решение. Запишем расширенную матрицу системы уравнений и последовательно преобразуем ее элементарными преобразованиями
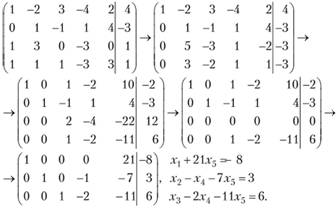
Таким образом, система совместна, имеет бесчисленное множество решений. Общее решение записывается в виде
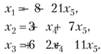
Любое частное решение получается из общего путем придания конкретных значений свободным переменным х4 и х5. Например, (-8; 4; 8; 1; 0) - частное решение. Одно из базисных решений получаем при х4 = 0 и х5 = 0 , т.е. (-8; 3; 6; 0; 0).
Число базисных решений не превосходит 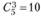 . Перейдем к другому базисному решению, взяв в расширенной матрице в качестве базисных решений векторы АиА2 ,А4 ; при этом переменные xt,x2 ,x4 будут базисными, а х3 ,х5 - свободными. Переход от одного базиса к другому осуществим методом Жордана - Гаусса, т.е. используя элементарные преобразования:
. Перейдем к другому базисному решению, взяв в расширенной матрице в качестве базисных решений векторы АиА2 ,А4 ; при этом переменные xt,x2 ,x4 будут базисными, а х3 ,х5 - свободными. Переход от одного базиса к другому осуществим методом Жордана - Гаусса, т.е. используя элементарные преобразования:
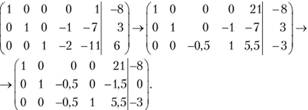
Таким образом, получено еще одно базисное решение: (-8; 0; 0; -3; 0) и т.д.
Заметим, что оба полученных базисных решения не являются опорными решениями; последнее решение является также вырожденным (базисная переменная х равна 0).
Рангом системы векторов
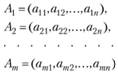
называется максимальное число линейно независимых векторов этой системы. Ранг системы векторов равен рангу матрицы А, составленной из компонент векторов этой системы, т.е. наивысшему порядку минора матрицы А, отличного от нуля.
Пример 2.4. Определить, является ли система векторов 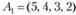 ,
, 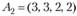 ,
, 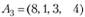 линейно зависимой; если она линейно-зависима, то найти ее максимальную линейно независимую подсистему.
линейно зависимой; если она линейно-зависима, то найти ее максимальную линейно независимую подсистему.
Решение. Составим матрицу из компонент векторов и найдем ее ранг.
Имеем 
Минор второго порядка 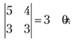
Рассмотрим два минора третьего порядка, которые его окаймляют:

Ранг матрицы А равен 2, поэтому система векторов является зависимой. В матрицах, составленных из компонент любых двух векторов данной системы, содержатся миноры второго порядка, отличные от нуля, например,
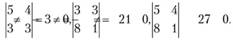
Поэтому максимальная линейно независимая подсистема состоит из двух любых векторов, а третий вектор является их линейной комбинацией.
Базисом n-мерного векторного пространства называется любая совокупность п линейно независимых векторов этого же пространства.
Теорема 2.2. Любой вектор n-мерного векторного пространства можно представить как линейную комбинацию векторов базиса, притом единственным образом.
Один из базисов n-мерного векторного пространства образует система единичных векторов
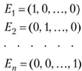
Компоненты любого n-мерного вектора можно считать координатами этого вектора в единичном базисе.
Пусть задано n-мерное линейное пространство 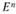
Определение 2.3. Множество X называется выпуклым, если вместе с любыми точками х{ и х2 множеству принадлежат точки (отрезок) 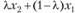 при всех
при всех 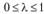
Множество на рис. 2.1, а - выпуклое, на рис. 2.1, б - невыпуклое.
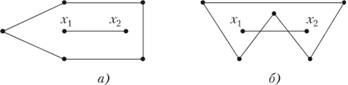
Рис. 2.1
Определение 2.4. Функция 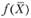 , заданная на выпуклом множестве
, заданная на выпуклом множестве  , называется выпуклой, если для любых двух точек x1 и х2 из X и любого числа
, называется выпуклой, если для любых двух точек x1 и х2 из X и любого числа 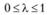 выполняется соотношение
выполняется соотношение
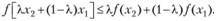
Определение 2.5. Функция 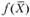 , заданная на выпуклом множестве
, заданная на выпуклом множестве 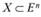 , называется вогнутой, если для любых двух точек х1 и х2 из X и любого числа
, называется вогнутой, если для любых двух точек х1 и х2 из X и любого числа 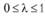 выполняется соотношение
выполняется соотношение
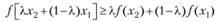
Если приведенные неравенства считать строгими и они выполняются при 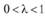 , то функция
, то функция 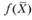 - строго выпуклая (вогнутая).
- строго выпуклая (вогнутая).
Можно показать, что если 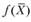 - выпуклая функция, то функция
- выпуклая функция, то функция 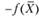 - вогнутая, и наоборот.
- вогнутая, и наоборот.
На рис. 2.2, а функция 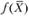 - выпуклая, на рис. 2.2, б - вогнутая.
- выпуклая, на рис. 2.2, б - вогнутая.
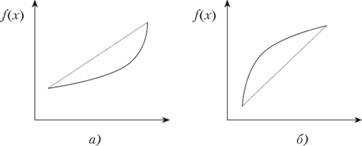
Рис. 2.2
Справедливы следующие утверждения относительно выпуклых множеств и функций.
1. Пересечение выпуклых множеств есть выпуклое множество.
2. Сумма вогнутых (выпуклых) функций есть вогнутая (выпуклая) функция.
3. Если 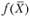 - выпуклая функция при
- выпуклая функция при 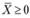 , то множество всех точек, удовлетворяющих условиям
, то множество всех точек, удовлетворяющих условиям 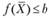 ,
, 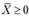 , выпукло (если оно не пустое; b - это постоянная).
, выпукло (если оно не пустое; b - это постоянная).
4. Пусть 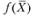 - выпуклая (вогнутая) функция, заданная на замкнутом выпуклом множестве
- выпуклая (вогнутая) функция, заданная на замкнутом выпуклом множестве  , тогда любой локальный минимум (максимум)
, тогда любой локальный минимум (максимум) 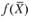 на X является и глобальным.
на X является и глобальным.
Приведем необходимое и достаточное условие выпуклости функции многих переменных. Пусть функция 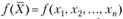 имеет все частные производные второго порядка, образующие матрицу
имеет все частные производные второго порядка, образующие матрицу
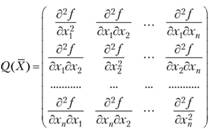
Эта функция является выпуклой в области X тогда и только тогда, когда матрица Q для любой точки из этой области является неотрицательно (положительно) определенной. Напомним, что квадратная матрица 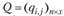 называется неотрицательно (положительно) определенной, если все определители
называется неотрицательно (положительно) определенной, если все определители

т.е. все главные миноры матрицы, неотрицательны (положительны).
Пример 2.5. Показать, что функция 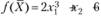 является выпуклой при
является выпуклой при 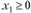
Составим матрицу из частных производных второго порядка для 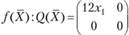
Найдем главные миноры 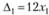 . Так как
. Так как 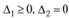 при
при 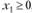 , то функция является выпуклой.
, то функция является выпуклой.
Дадим определение глобального и локального максимумов. Функция 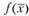 достигает на замкнутом (т.е. включающем свою границу) множестве X глобальный максимум в точке
достигает на замкнутом (т.е. включающем свою границу) множестве X глобальный максимум в точке 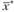 , если для любой точки, принадлежащей
, если для любой точки, принадлежащей 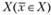 , выполняется условие
, выполняется условие 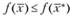
Функция 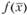 достигает на замкнутом множестве X локального максимума в точке
достигает на замкнутом множестве X локального максимума в точке 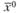 , если существует некоторой окрестность этой точки, для каждой точки которой выполняется условие
, если существует некоторой окрестность этой точки, для каждой точки которой выполняется условие 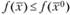
Определения локального и глобального минимума формулируются аналогично.
На рис. 2.3 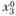 - точка локального минимума;
- точка локального минимума; 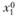 - глобального минимума; α,
- глобального минимума; α, 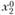 - точки локального максимума; β - точка глобального максимума.
- точки локального максимума; β - точка глобального максимума.
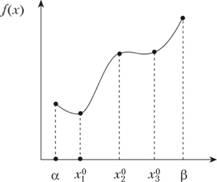
Рис. 2.3
Необходимые условия экстремума (максимума, минимума). Если в точке 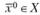 функция
функция 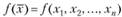 имеет экстремум, то частные производные первого порядка равны нулю в этой точке:
имеет экстремум, то частные производные первого порядка равны нулю в этой точке:
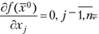
Достаточные условия существования экстремума здесь не формулируются. О самом существовании точек глобального минимума и максимума говорит следующая теорема.
Теорема Вейерштрасса
Если функция 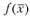 определена и непрерывна в ограниченной замкнутой области X, то она достигает в ней своих точных верхней и нижней границ (глобальный максимум и глобальный минимум).
определена и непрерывна в ограниченной замкнутой области X, то она достигает в ней своих точных верхней и нижней границ (глобальный максимум и глобальный минимум).
Приведенные утверждения относительно выпуклых множеств и функций, условий существования экстремума позволяют делать выводы о свойствах тех или иных задач оптимального программирования, что является основой разработки и применения математических методов их решения. Например, симплекс-метод решения задачи линейного программирования использует, в частности, "свойство выпуклости" этой задачи: не существует локального экстремума, отличного от глобального.
Таблица 2.1
Таблица 2.2
Решение ЗЛП в симплекс-таблицах
| Номер симплекс- таблицы | Базис | ci / cj | План В | 2 | 3 | 0 | 0 | Q |
| A1 | A2 | A3 | A4 | |||||
| 0 | А3 | 0 | 300 | 1 | 3 | 1 | 0 | 100 |
| А4 | 0 | 150 | 1 | 1 | 0 | 1 | 150 | |
| ∆j | - | 0 | -2 | -3 | 0 | 0 | - | |
| I | A2 | 3 | 100 | 1/3 | 1 | 1/3 | 0 | 300 |
| A4 | 0 | 50 | 2/3 | 0 | -1/3 | 1 | 75 | |
| ∆j | - | 300 | -1 | 0 | 1 | 0 | - | |
| II | A2 | 3 | 75 | 0 | 1 | 1/2 | -1/2 | |
| A1 | 2 | 75 | 1 | 0 | -1/2 | 3/2 | ||
| ∆j | - | 375 | 0 | 0 | 1/2 | 3/2 | - |
Второй опорный план (0, 100, 0, 50) не оптимальный; переход к следующему опорному плану осуществим, вводя в базис вектор A1 и выводя вектор А4.
В симплекс-таблице II получен оптимальный опорный план, поскольку все симплекс-разности (оценки) 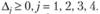 Оптимальные значения переменных равны:
Оптимальные значения переменных равны: 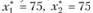 (основные переменные),
(основные переменные), 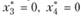 (дополнительные переменные).
(дополнительные переменные).
Максимальное значение целевой функции равно 375.
Таким образом, в рассмотренной задаче об оптимальном использовании ограниченных ресурсов, оптимальная производственная программа состоит в выпуске 75 ед. продукции первого вида и 75 ед. продукции второго вида. С этой программой связана максимальная прибыль от реализации готовой продукции - 375 у.е.
Симплекс-метод с искусственным базисом (М-метод)
Применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи ЛП, записанной в канонической форме.
М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной ЗЛП таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае ее максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М - достаточно большое положительное число.
В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки ∆j теперь будет зависеть "от буквы М". Для сравнения оценок нужно помнить, что М - достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
В процессе решения М-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М-задачи содержит искусственные векторы или М-задача неразрешима, то исходная задача также неразрешима.
Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.
Пример 2.8. Найти максимум целевой функции: 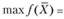
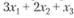 при условиях
при условиях
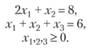
Решение. Матрица условий содержит только один единичный вектор, добавим еще один искусственный вектор (искусственную неотрицательную переменную ух в первое ограничение):
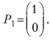
Получим следующую М-задачу: найти максимум целевой функции 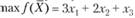 - Му1 при условиях
- Му1 при условиях
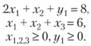
М-задачу решаем симплекс-методом. Начальный опорный план (0, 0, 6, 8), решение проводим в симплекс-таблицах (табл. 2.3).
В начальной таблице наименьшее ∆j соответствует вектору А1 - он вводится в базис, а искусственный вектор P1 из базиса выводится, так как ему отвечает наименьшее Q. Столбец, соответствующий Р1, из дальнейших симплексных таблиц вычеркивается.
Таблица 2.3
Решение М-задачи в симплекс-таблицах
| Номер симплекс- таблицы | Базис | ci / cj | План В | 3 | 2 | 1 | -M | Q |
| A1 | A2 | A3 | P1 | |||||
| 0 | P1 | -M | 8 | 2 | 1 | 0 | 1 | 4 |
| A3 | 1 | 6 | 1 | 1 | 1 | 0 | 6 | |
| ∆j | - | -8М+6 | -2М-2 | -М-1 | 0 | 0 | - | |
| 1 | A1 | 3 | 4 | 1 | 0,5 | 0 | - | |
| A3 | 1 | 2 | 0 | 0,5 | 1 | - | ||
| ∆j | - | 14 | 0 | 0 | 0 | - |
Полученный новый опорный план является опорным планом исходной задачи. Для него все ∆j > 0, поэтому он является и оптимальным. Таким образом, получен оптимальный план исходной задачи (4, 0, 2) и максимальное значение целевой функции max 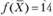 .
.
Пример 2.9. Решить ЗЛП:
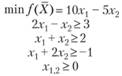
Решение. Приведем ЗЛП к каноническому виду, перейдя к задаче "на максимум":
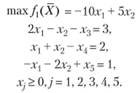
Для нахождения опорного плана переходим к М-задаче:
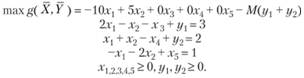
Дальнейшее решение проводим в симплекс-таблицах (табл. 2.4).
Таблица 2.4
Решение ЗЛП М-методом
| Номер симплекс-таблицы | Базис | ci / cj | В | -10 | 5 | 0 | 0 | 0 | -M | -M | Q |
| A1 | A2 | A3 | A4 | A5 | P1 | P2 | |||||
| 0 | P1 | -M | 3 | 2 | -1 | -1 | 0 | 0 | 1 | 0 | 3/2 |
| P2 | -M | 2 | 1 | 1 | 0 | -1 | 0 | 1 | 1 | 2 | |
| A5 | 0 | 1 | -1 | -2 | 0 | 0 | 0 | 0 | 0 | - | |
| - | ∆j | - | -5 М | -3 М+ + 10 | -5 | М | М | 0 | - | ||
| I | A1 | -10 | 3/2 | 1 | -1/2 | -1/2 | 0 | 0 | 0 | - | |
| P2 | -M | 1/2 | 0 | 3/2 | 1/2 | -1 | 0 | 1 | 1/3 | ||
| A5 | 0 | 5/2 | 0 | -5/2 | -1/2 | 0 | 1 | 0 | - | ||
| - | ∆j | - | -M/2-15 | 0 | -3М/2 | -М/2+5 | М | 0 | 0 | - | |
| II | A1 | -10 | 5/3 | 1 | 0 | -1/3 | -1/3 | 0 | - | ||
| A2 | 5 | 1/3 | 0 | 1 | 1/3 | -2/3 | 0 | - | |||
| A5 | 0 | 10/3 | 0 | 0 | 0 | -5/3 | 1 | - | |||
| - | ∆j | - | -15 | 0 | 0 | 5 | 0 | 0 | - |
В симплекс-таблице II получен опорный план исходной ЗЛП; поскольку все симплекс-разности 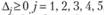 , то этот план является и оптимальным, т.е.
, то этот план является и оптимальным, т.е. 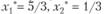 (исходные переменные),
(исходные переменные), 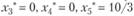 (дополнительные переменные), при этом
(дополнительные переменные), при этом 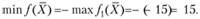
При рассмотрении графического метода выделялись три особых случая решения ЗЛП. В симплекс-методе эти случаи определяются следующим образом.
1. Если найден оптимальный план и оценки всех свободных переменных строго больше нуля, то оптимальный план является единственным', если оценки некоторых свободных переменных в оптимальном плане равны нулю, то этот план будет неединственным, так как ввод этих переменных в базис не нарушает критерия оптимальности и не меняет оптимальное значение целевой функции. В соответствии с этим оптимальный план в табл. 2.2 является единственным, а в табл. 2.3 и 2.4 - несдинственным (первый особый случай).
2. Если в процессе решения ЗЛП М-методом искусственные переменные не выводятся из базиса, это является свидетельством того, что область определения исходной ЗЛП является пустым множеством: в этом случае ЗЛП не имеет решения ввиду противоречивости системы ограничений (второй особый случай).
3. Если в направляющем столбце все элементы ajk неположительны (см. 2.23), то это свидетельствует о незамкнутости области определения ЗЛП; в этом случае ЗЛП не имеет решения ввиду неограниченности целевой функции (третий особый случай).
Для автоматизации решения задач линейного программирования могут быть использованы стандартные офисные средства Microsoft Excel - надстройка Поиск решения, использующая симплексный метод (линейная оптимизация с помощью надстройки Поиск решения подробно рассмотрена, например, в литературе).
Однако для корректного и эффективного использования программных средств необходимо знать основы линейного программирования, изложенные выше в данной главе.
Лекция 2 Основы линейного программирования
- Принцип оптимальности в планировании и управлении, общая задача оптимального программирования
- Формы записи задачи линейного программирования и ее экономическая интерпретация
- Математический аппарат линейного программирования
- Геометрическая интерпретация задачи
- Симплексный метод решения задачи
После изучения данной главы студенты должны:
знать:
o общие принципы оптимального планирования и управления в экономике:
o основные понятия линейного программирования:
o методы решения задач линейного программирования (ЗЛП);
уметь:
o формулировать общую постановку ЗЛП;
o представить ЗЛП в различных формах записи;
o дать экономическую интерпретацию полученных результатов на всех этапах графического и симплексного методов решения ЗЛП;
владеть:
o математическим аппаратом линейного программирования;
o практическими навыками формулирования и решения ЗЛП.
Принцип оптимальности в планировании и управлении, общая задача оптимального программирования
Линейное программирование - это особый раздел оптимального программирования. В свою очередь оптимальное (математическое) программирование - раздел прикладной математики, изучающий задачи условной оптимизации. В экономике такие задачи возникают при практической реализации принципа оптимальности в планировании и управлении.
Необходимым условием использования оптимального подхода к планированию и управлению (принципа оптимальности) является гибкость, альтернативность производственно-хозяйственных ситуаций, в условиях которых приходится принимать планово-управленческие решения. Именно такие ситуации, как правило, и составляют повседневную практику хозяйствующего субъекта (выбор производственной программы, прикрепление к поставщикам, маршрутизация, раскрой материалов, приготовление смесей, загрузка контейнеров и т.д.).
Суть принципа оптимальности состоит в стремлении выбрать такое планово-управленческое решение 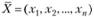 , где
, где 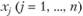 - его компоненты, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта.
- его компоненты, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта.
Слова "наилучшим образом" здесь означают выбор некоторого критерия оптимальности, т.е. некоторого экономического показателя, позволяющего сравнивать эффективность тех или иных планово-управленческих решений. Традиционные критерии оптимальности: "максимум прибыли", "минимум затрат", "максимум объема работ (услуг)" и др.
Слова "учитывало бы внутренние возможности и внешние условия производственной деятельности" означают, что на выбор управленческого решения (поведения) накладывается ряд условий, т.е. выбор 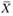 осуществляется из некоторой области возможных (допустимых) решений D; эту область называют также областью определения задачи.
осуществляется из некоторой области возможных (допустимых) решений D; эту область называют также областью определения задачи.
Таким образом, реализовать на практике принцип оптимальности в планировании и управлении - это значит решить экстремальную задачу вида
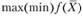 (2.1)
(2.1)
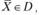 (2.2)
(2.2)
где 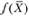 - математическая запись критерия оптимальности - целевая функция задачи (модели) оптимизации.
- математическая запись критерия оптимальности - целевая функция задачи (модели) оптимизации.
Задачу условной оптимизации (2.1), (2.2) обычно записывают в виде:
найти максимум или минимум функции
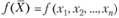 (2.3)
(2.3)
при ограничениях
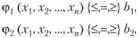 (2.4)
(2.4)
………………………..
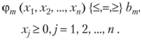 (2.5)
(2.5)
Условие (2.5) необязательно, но его всегда при необходимости можно добиться. Обозначение {≤,=,≥} говорит о том, что в конкретном ограничении возможен один из знаков ≤, = или ≥. Более компактная запись:
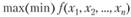 (2.6)
(2.6)
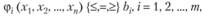 (2.7)
(2.7)
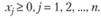 (2.8)
(2.8)
Задача (2.6)-(2.8) - общая задача оптимального (математического) программирования, иначе - математическая модель задачи оптимального программирования, в основе построения (разработки) которой лежат принципы оптимальности, системности и адекватности.
Вектор 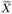 (набор управляющих переменных хj, j = 1, 2, ..., п) называется допустимым решением или планом задачи оптимального программирования, если его компоненты xj удовлетворяют системе ограничений. А тот план
(набор управляющих переменных хj, j = 1, 2, ..., п) называется допустимым решением или планом задачи оптимального программирования, если его компоненты xj удовлетворяют системе ограничений. А тот план 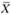 (допустимое решение), который доставляет максимум или минимум целевой функции f(x1, х2, ..., хn) называется оптимальным планом (оптимальным поведением, или просто решением) задачи оптимального программирования.
(допустимое решение), который доставляет максимум или минимум целевой функции f(x1, х2, ..., хn) называется оптимальным планом (оптимальным поведением, или просто решением) задачи оптимального программирования.
Таким образом, выбор оптимального управленческого поведения в конкретной производственной ситуации связан с проведением с позиций системности, адекватности и оптимальности экономико-математического моделирования и решением задачи оптимального программирования.
Решить задачу оптимального программирования (получить решение по оптимизационной экономико-математической модели) - это значит:
- во-первых, найти оптимальный план 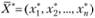 ,
,
который, с учетом интерпретации его компонент, и определяет оптимальное поведение в рассматриваемой ситуации;
- во-вторых, найти оптимальное значение (максимум или минимум) целевой функции 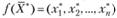 , которое и представляет собой экономическую оценку последствий предлагаемого решения (поведения).
, которое и представляет собой экономическую оценку последствий предлагаемого решения (поведения).
Иногда невозможно получить решение по оптимизационной модели: область допустимых решений может оказаться пустым множеством (задача противоречива) или целевая функция является неограниченной на области определения.
Первый случай связан с некорректностями в постановке экономической задачи или (и) разработанной экономико-математической модели (ЭММ). Например, с имеющимся объемом ресурсов заведомо невозможно выполнить даже те минимальные объемы работ, которые закладываются в ограничения как необходимые минимальные плановые задания. Если в данной ситуации все же необходимо найти решение задачи, то следует построить непустое множество допустимых решений, исключив одно или несколько ограничений, т.е. фактически соблюсти принцип альтернативности.
Второй случай обычно означает, что ЭММ разработана некорректно и некоторые существенные ограничения в ней отсутствуют.
Задачи оптимального программирования в наиболее общем виде классифицируют по следующим признакам.
1. По характеру взаимосвязи между переменными:
а) линейные;
б) нелинейные.
В случае (а) все функциональные связи в системе ограничений и функция цели - линейные функции, наличие нелинейности в хотя бы одном из упомянутых элементов приводит к случаю (б).
2. По характеру изменения переменных:
а) непрерывные;
б) дискретные.
В случае (а) значения каждой из управляющих переменных могут заполнять сплошь некоторую область действительных чисел, в случае (б) все или хотя бы одна переменная могут принимать только целочисленные значения.
3. По учету фактора времени:
а) статические;
б) динамические.
В задачах (а) моделирование и принятие решений осуществляются в предположении о независимости от времени элементов модели в течение периода времени, на который принимается планово-управленческое решение. В случае (б) такое предположение достаточно аргументированно принято не может быть и необходимо учитывать фактор времени.
1. По наличию информации о переменных:
а) задачи в условиях полной определенности (детерминированные);
б) задачи в условиях неполной информации;
в) задачи в условиях неопределенности.
В задачах (б) отдельные элементы являются вероятностными величинами, однако известны или дополнительными статистическими исследованиями могут быть установлены их законы распределения вероятностей. В случае (в) можно сделать предположение о возможных исходах случайных элементов, но нет возможности сделать вывод о вероятностях исходов.
2. По числу критериев оценки альтернатив:
а) простые, однокритериальные задачи;
б) сложные, многокритериальные задачи.
В задачах (а) экономически приемлемо использование одного критерия оптимальности или удастся специальными процедурами (например, "взвешиванием приоритетов") свести многокритериальный поиск к однокритериальному; примеры многокритериальных задач рассмотрены в главе 3.
Сочетание признаков 1-5 позволяет группировать (классифицировать) в самом общем виде задачи и методы оптимального программирования, например: 1а)2а)3а)4а)5а) - задачи и методы линейного программирования, 1б)2а)3а)4а)5а) - задачи и методы нелинейного программирования, 1а)2б)3а)4а)5а) - задачи и методы целочисленного (дискретного) линейного программирования и т.д.
Новые возможности для широкого практического применения методов оптимального программирования представляют современные офисные средства. Широкий круг специалистов в своей повседневной практике использует необходимый компонент финансово-экономических расчетов - Microsoft Excel (MS Excel), который содержит специальное средство - надстройку Поиск решения, позволяющую реализовывать модели линейной, нелинейной и дискретной оптимизации. Технология оптимизации с помощью надстройки Поиск решения с решением некоторых типовых задач оптимального программирования в среде MS Excel подробно рассмотрена, например, в литературе.
Рассмотрим пример задачи оптимального программирования.
Постановка задачи. Предлагается п инвестиционных проектов, тщательная экономическая экспертиза которых позволяет получить для каждого из проектов достаточно убедительные экономические оценки ожидаемого эффекта от их реализации с1, с2, ..., сn и необходимых капиталовложений р1, р2, ..., pn. Общий объем возможных капиталовложений ограничен величиной В. Необходимо так распорядиться имеющимися финансовыми ресурсами, чтобы максимизировать суммарный эффект от инвестиций.
Математическая модель. Введем необходимые обозначения, пусть хj(j = 1, 2, ..., п):

Таким образом, формально инвестиционный план - это вектор X=(х1, х2, ..., хn). С учетом этих обозначений задача по критерию "максимум экономического эффекта" математически запишется следующим образом:
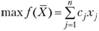
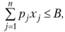
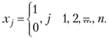
Приведенная задача (модель) является задачей дискретного линейного программирования с булевыми переменными (переменные, которые могут принимать только два значения: 1 и 0, иначе "да" или "нет"), т.е. относится к классу задач 1а)2б)3а)4а)5а). Эта задача может быть решена, например, известным методом Балаша.
Выбору метода решения конкретной задачи оптимального программирования предшествует ее классификация, т.е. отнесение к одному из классов оптимизационных задач, начиная с приведенных самых общих признаков (например, задача дискретного линейного программирования с булевыми переменными).
Развитие и совершенствование методов решения задач оптимального программирования идет от случаев типа (а) к случаям типа (б), (в).
Наиболее изучены задачи линейного программирования, для которых разработан универсальный метод решения - метод последовательного улучшения плана (симплекс-метод), т.е. любая задача линейного программирования решается (о модели линейной оптимизации говорят, что она реализуется) этим методом.
Именно эти задачи в дальнейшем рассматриваются в данной главе.
Дата: 2019-03-05, просмотров: 408.