Изучение и понимание современных экономико-математических методов предполагает достаточно серьезную математическую подготовку экономистов. Для освоения задач и методов в пределах данной главы необходимы знания основных понятий и элементов высшей математики, матричной и векторной алгебры. Некоторые необходимые сведения из этих разделов математики приведены ниже.

Матрицы и определители

Рассмотрим т x п действительных чисел, записанных в виде прямоугольной таблицы из т строк и п столбцов:

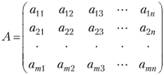
Данная таблица чисел называется числовой матрицей (в дальнейшем - просто матрицей). Числа а_ij, которые входят в матрицу, называются ее элементами. Индексы i и j элемента a_ij указывают соответственно номера строки и столбца, в которых расположен элемент a_ij. Матрицу, содержащую одну строку (или один столбец), называют также вектор-строкой (или вектор-столбцом).

Матрица, все элементы которой равны нулю, называется нулевой. Две матрицы называются равными, если числа строк и столбцов одной из них равны соответственно числам строк и столбцов другой и элементы этих матриц, расположенные на соответствующих местах, равны.

Матрицей, транспонированной к матрице А, называется матрица вида

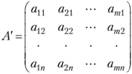
т.е. строками матрицы А являются столбцы, а столбцами - строки матрицы А.

Если число строк равно числу столбцов (т = n), матрицу называют квадратной матрицей порядка п.

Элементы а₁₁, а₂₂, a₃₃, а_nn, образуют так называемую главную диагональ квадратной матрицы; элементы a_1n, а_2n-1, ..., а_n1 - побочную диагональ квадратной матрицы.

Рассмотрим некоторые действия над матрицами.

1. Произведением матрицы А на число λ (или, что то же самое, числа λ на матрицу А) называется матрица

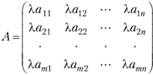
получающаяся из А путем умножения каждого ее элемента на число λ.

2. Под суммой двух матриц

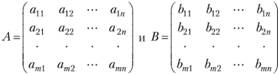
элементы которой равны суммам соответствующих элементов матриц А и В. При этом подразумевается, что число строк (столбцов) матрицы А равно числу строк (столбцов) матрицы В. Подобным же образом определяется и разность (А - В) матриц А и В.

Линейные операции над матрицами подчиняются обычным законам арифметики, например:

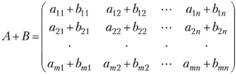
понимается матрица

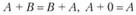
(все элементы матрицы 0 - нули),

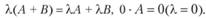
3. Произведением матрицы А из т строк и п столбцов на матрицу В из п строк и k столбцов называется матрица С = АВ, имеющая т строк и k столбцов, элемент С_ij которой, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-гo столбца матрицы В, т.е. находится по формуле скалярного произведения i-й вектор-строки матрицы А на j-й вектор-столбец матрицы В:

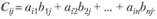
В случае квадратных матриц можно составить как произведение АВ, так и произведение ВА. В общем случае АВ≠ВА, т.е. переместительный закон для матриц не выполняется.

Для произведения матриц остаются в силе следующие законы арифметики.

1. Распределительный закон (А + В)С = АС + ВС, С(А + В) = СА + СВ.

2. Сочетательный закон (АВ)С = А(ВС).

Среди квадратных матриц особую роль играет матрица

все элементы которой, расположенные на главной диагонали, равны единице, а остальные - нулю. Можно проверить, что для любой матрицы А:

АЕ = ЕА = А. Матрица Е называется единичной.

Матрица В называется обратной для матрицы А, если АВ = ВА = Е. Матрица В, обратная матрице А, обозначается через A^-1 (функция = МОБР() Мастера функций MS Excel).

С каждой квадратной матрицей определенным образом связано некоторое число, называемое ее определителем (функция =МОПРЕД() Мастера функций MS Excel).

Для вычисления определителя любого порядка необходимо знание его свойств и теоремы о разложении определителя.

Приведем основные свойства определителей.

1. При транспонировании матрицы ее определитель не меняется. Это свойство свидетельствует о полном равноправии строк и столбцов определителя. Следовательно, если некоторое утверждение справедливо относительно столбцов определителя, то аналогичное утверждение справедливо и для его строк.

2. Если все элементы какого-либо столбца (строки) определителя равны нулю, то и сам определитель равен нулю.

3. При перестановке двух любых столбцов (строк) определителя его знак меняется на противоположный, а абсолютная величина остается неизменной.

4. Определитель с двумя одинаковыми столбцами (строками) равен нулю.

5. Если j-й столбец (строка) A_j определителя D является линейной комбинацией

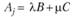
двух произвольных столбцов (строк) В и С, то и сам определитель оказывается линейной комбинацией

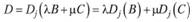
определителей D_j(B) и D_j(C).

Здесь Dj(B) и D_j(С) - определитель D, в котором столбец (строка) у заменен соответственно на столбец (строку) В и С. Остальные столбцы (строки) сохранены без изменения.

6. При умножении любого столбца (строки) определителя на произвольное число λ сам определитель умножается на это же число.

7. Если какой-либо столбец (строка) определителя является линейной комбинацией других его столбцов (строк), то определитель равен нулю.

8. Определитель не изменится, если к элементам любого его столбца (строки) прибавить соответствующие элементы другого столбца (строки), предварительно умноженные на одно и то же число.

Рассмотрим определитель n-го порядка:

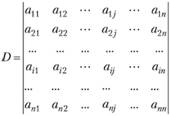
Выделим в нем некоторый элемент, например a_ij. Вычеркнем в определителе i-ю строку и j-й столбец, в которых расположен выделенный элемент а_ij. В результате останется определитель (n-1)-го порядка. Этот оставшийся определитель называется минором элемента а_ij в определителе D и обозначается М_ij.

Величину 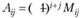называют алгебраическим дополнением элемента a_ij в определителе D (или в соответствующей квадратной матрице).