П.1. Сведение двойного интеграла по прямоугольнику к повторному интегралу
Теорема 1 Пусть 1) функция 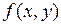 интегрируема на прямоугольнике
интегрируема на прямоугольнике 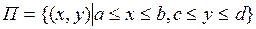 ; 2)
; 2) 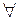
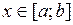 существует интеграл
существует интеграл 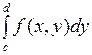 . Тогда функция
. Тогда функция 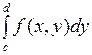 - интегрируема на
- интегрируема на 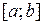 , причем
, причем 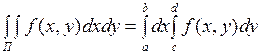 .
.
Следствие 1 Пусть 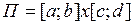 ,
, 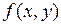 интегрируема на
интегрируема на 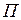 . Если
. Если 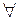
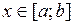
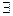
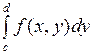 и
и 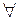
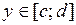
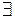
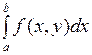 , тогда
, тогда
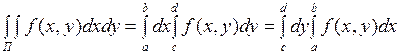 (1)
(1)
Следствие 2 Если 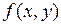 - непрерывна на
- непрерывна на 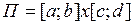 , то верны условия следствия 1, и равенство (1) выполняется.
, то верны условия следствия 1, и равенство (1) выполняется.
П.2 Сведение двойного интеграла по элементарной области
К повторному интегралу
Пусть 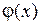 и
и 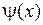 − непрерывны на
− непрерывны на 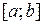 и
и 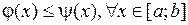 .
.
Область 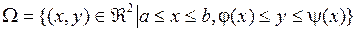 называется элементарной относительно оси
называется элементарной относительно оси 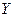 . Это множество является измеримым по Жордану, т.к. ограничено кривыми и отрезками.
. Это множество является измеримым по Жордану, т.к. ограничено кривыми и отрезками.
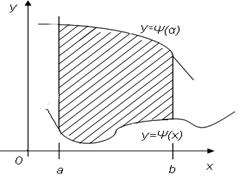
Теорема 2 Пусть 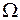 элементарная относительно оси
элементарная относительно оси 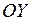 область, функция
область, функция 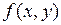 интегрируема на
интегрируема на 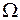 и
и 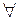
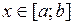
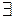
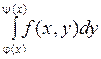 , тогда
, тогда
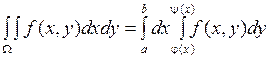 . (2)
. (2)
Следствие Если 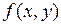 непрерывна на
непрерывна на 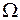 , то справедлива формула (2).
, то справедлива формула (2).
Пример Вычислить 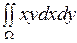 , если
, если 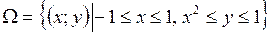 .
.
Опр. Определим область, элементарную относительно оси 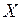 − это множество
− это множество 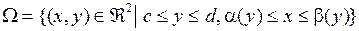 .
.
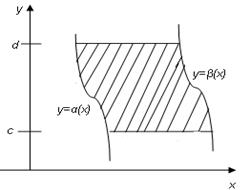
Теорема 3 Если 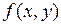 непрерывна в области
непрерывна в области 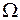 , элементарной относительно оси
, элементарной относительно оси 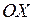 , то
, то 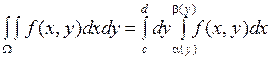 .
.
П.3 Сведение тройных интегралов к повторным
Область 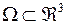 называется элементарной относительно оси
называется элементарной относительно оси 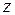 , если:
, если: 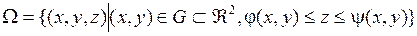 , где
, где 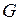 − замкнутое и ограниченное множество в
− замкнутое и ограниченное множество в 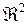 , функции
, функции 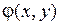 и
и 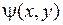 − непрерывные.
− непрерывные.
Теорема 4 Если функция 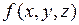 − непрерывна в области
− непрерывна в области 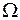 , элементарной относительно оси
, элементарной относительно оси 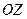 , то
, то 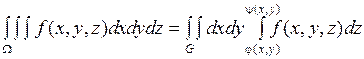 .
.

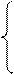
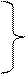 Если при этом
Если при этом  =
= 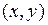
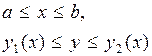 ,
,
то 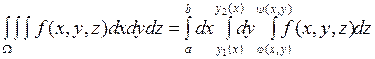 .
.
Пример 1 Расставить пределы интегрирования в повторном интеграле 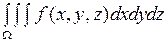 , если
, если 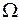 − область, ограниченная параболоидом
− область, ограниченная параболоидом 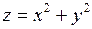 и плоскостью
и плоскостью 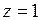 . Ответ:
. Ответ: 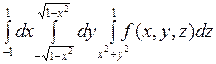 .
.
Пример 2 Вычислить 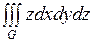 по области
по области  , ограниченной плоскостями
, ограниченной плоскостями 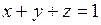 ,
, 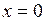 ,
, 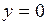 ,
, 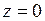 .
.
Замена переменных в кратном интеграле
П.1 Двойные интегралы
Рассмотрим 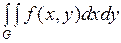 . Перейдем от переменных
. Перейдем от переменных 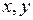 к переменным
к переменным 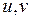 по формулам:
по формулам: 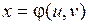 ,
, 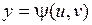 ,
, 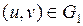 .
.
При этом отображении каждой точке 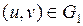 соответствует некоторая точка
соответствует некоторая точка 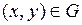 . (Т.е. если точка (
. (Т.е. если точка ( 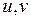 ) пробегает область
) пробегает область 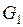 , то (
, то ( 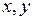 ) пробегает область
) пробегает область 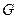 .) Область
.) Область  является образом
является образом 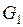 при данном отображении.
при данном отображении.
Пусть отображение 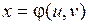 ,
, 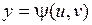 ,
, 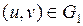 (1) удовлетворяет следующим условиям:
(1) удовлетворяет следующим условиям:
1) Отображение (1) взаимно однозначно (т.е. различные точки области 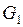 переходят в различные точки области
переходят в различные точки области  );
);
2) Функции 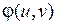 и
и 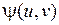 имеют непрерывные частные производные первого порядка в области
имеют непрерывные частные производные первого порядка в области 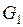 ;
;
3) 
 Якобиан отображения
Якобиан отображения 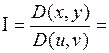
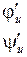
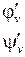 ≠ 0 в
≠ 0 в 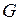 .
.
Теорема Пусть  и
и 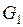 - замкнутые ограниченные множества, функция
- замкнутые ограниченные множества, функция 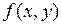 ограничена в области
ограничена в области  и непрерывна всюду, кроме, быть может, некоторого множества меры 0, а отображение (1) удовлетворяет условиям 1-3. Тогда справедливо равенство
и непрерывна всюду, кроме, быть может, некоторого множества меры 0, а отображение (1) удовлетворяет условиям 1-3. Тогда справедливо равенство
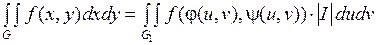 .
.
Замечание 1 Отображение, удовлетворяющее условиям 1-3, обладает следующими свойствами:
1) непрерывные кривые при этом отображении переходят в непрерывные кривые;
2) граница области 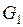 переходит в границу области
переходит в границу области  .
.
Замечание 2
Если условие 1 (взаимная однозначность отображения (1)) или условие 3 (неравенство нулю Якобиана) нарушается на множестве меры 0 (например, в отдельных точках или на отдельных кривых), то формула замены переменных остается в силе.
Пример Вычислить 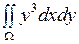 , если
, если  ограничена кривыми:
ограничена кривыми: 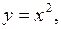
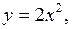
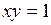 ,
, 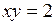 .
.
Решение. Замена 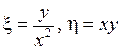 . Тогда
. Тогда 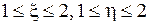 .
.
Выразим 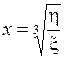 ,
, 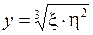 .
.
Якобиан I = 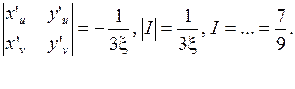
Дата: 2019-03-05, просмотров: 361.