Пусть множество G измеримо по Жордану в 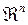 .
.
Опр. Разбиением множества G называется совокупность измеримых по Жордану в 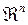 и попарно непересекающихся множеств
и попарно непересекающихся множеств 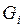 ,
, 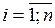 , если
, если 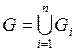 .
.
Разбиение будем обозначать буквой Т,  – диаметр множества
– диаметр множества 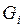 . Число
. Число 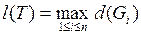 называется мелкостью разбиения.
называется мелкостью разбиения.
Опр. Пусть функция f(x) определена на измеримом по Жордану множестве 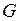 ,
, 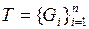 − разбиение множества
− разбиение множества 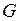 .
.
Возьмем в каждом множестве 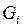 произвольную точку
произвольную точку  .
.
Выражение 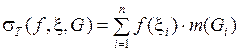 называется интегральной суммой Римана функции f(x) на множестве
называется интегральной суммой Римана функции f(x) на множестве 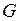 , соответствующей разбиению T и выборке
, соответствующей разбиению T и выборке  .
.
Опр. Число I называется пределом интегральных сумм 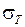 при мелкости разбиения
при мелкости разбиения  , если
, если 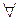
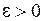
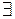
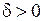 , такое, что для любого разбиения с мелкостью
, такое, что для любого разбиения с мелкостью  и при любом выборе точек
и при любом выборе точек 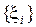 выполняется неравенство
выполняется неравенство
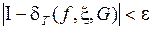 .
.
Если число I является пределом интегральных сумм при  , то число I называют кратным интегралом Римана от функции f(x) по множеству
, то число I называют кратным интегралом Римана от функции f(x) по множеству 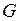 , а функцию f(x) − интегрируемой по множеству
, а функцию f(x) − интегрируемой по множеству 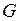 .
.
Обозначается 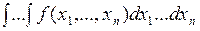 или
или 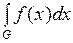
 .
.
В случае 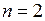 интеграл называется двойным, а в случае
интеграл называется двойным, а в случае 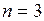 − тройным. Обозначается …
− тройным. Обозначается …
Прежде, чем сформулировать теорему, введем определение.
Если f(x) ограничена на множестве 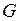 , то для
, то для 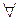 разбиения T определены числа
разбиения T определены числа 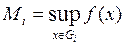 и
и 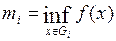 .
.
Выражения  и
и 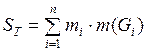 называются соответственно верхней и нижней суммами Дарбу, соответствующими разбиению Т.
называются соответственно верхней и нижней суммами Дарбу, соответствующими разбиению Т.
Теорема (критерий интегрируемости)
Ограниченная функция 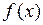 интегрируема по множеству
интегрируема по множеству 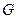 тогда и только тогда, когда
тогда и только тогда, когда 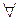
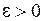
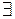
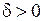 : для любого разбиения с мелкостью
: для любого разбиения с мелкостью  выполняется неравенство
выполняется неравенство  , т.е.
, т.е. 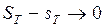 при
при 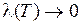 .
.
П.3. Классы интегрируемых функций
Теорема 1 Непрерывная на измеримом по Жордану компакте функция интегрируема на нем.
Теорема 2 Пусть функция 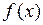 ограничена на измеримом по Жордану компакте
ограничена на измеримом по Жордану компакте  и множество ее точек разрыва имеет Жорданову меру 0, тогда
и множество ее точек разрыва имеет Жорданову меру 0, тогда 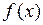 интегрируема на множестве
интегрируема на множестве 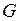 .
.
Доказательство. Пусть Е − множество точек разрыва функции 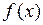 и
и 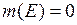 . Тогда
. Тогда 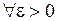 существует открытое клеточное множество А, такое, что
существует открытое клеточное множество А, такое, что 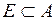 и
и 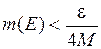 , где
, где 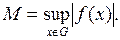
На множестве 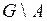 (а оно замкнуто и ограничено)
(а оно замкнуто и ограничено) 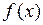 непрерывна, следовательно, интегрируема. Значит,
непрерывна, следовательно, интегрируема. Значит, 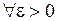 существует разбиение
существует разбиение 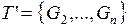 множества
множества 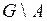 такое, что
такое, что
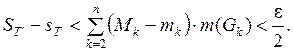
Пусть 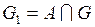 . Тогда множества
. Тогда множества 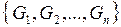 образуют разбиение Т множества
образуют разбиение Т множества 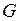 , причем
, причем 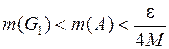 .
.
Тогда 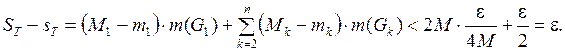
П.4. Свойства кратного интеграла
1) Справедливо равенство 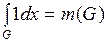 .
.
2) Если 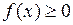 и
и 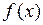 интегрируема на множестве
интегрируема на множестве 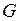 , то
, то 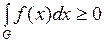 .
.
3) Если 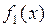 и
и 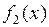 интегрируемы на множестве
интегрируемы на множестве 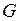 , то
, то 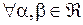
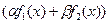 − интегрируема на множестве
− интегрируема на множестве 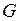 , причем
, причем
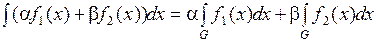 .
.
4) Если 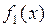 и
и 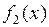 интегрируемы на множестве
интегрируемы на множестве 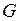 и
и 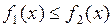 ,
, 
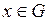 , то
, то  .
.
5) Теорема о среднем. Если 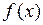 – непрерывна на связном компакте
– непрерывна на связном компакте 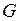 , то
, то
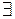
 :
: 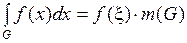 .
.
6) Если 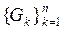 − разбиение множества
− разбиение множества 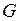 , причем
, причем 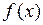 интегрируема на каждом
интегрируема на каждом 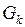 , то
, то 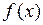 интегрируема на множестве
интегрируема на множестве 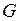 , причем
, причем
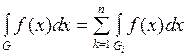 .
.
7) Произведение интегрируемых на 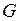 функций, есть интегрируемая на
функций, есть интегрируемая на 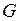 функция.
функция.
8) Если 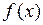 интегрируема на множестве
интегрируема на множестве 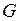 , то
, то 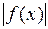 тоже интегрируема на
тоже интегрируема на 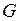 , причем
, причем 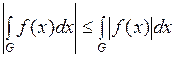 .
.
Дата: 2019-03-05, просмотров: 330.