Свойства множеств жордановой меры 0.
1) Множество меры 0 измеримо по Жордану (по определению).
2) Объединение конечного числа множеств меры 0 есть множество меры 0.
3) Подмножество множества меры 0 есть множество меры 0.
П.2. Определение кратного интеграла Римана
Пусть множество G измеримо по Жордану в 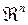 .
.
Опр. Разбиением множества G называется совокупность измеримых по Жордану в 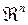 и попарно непересекающихся множеств
и попарно непересекающихся множеств 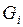 ,
, 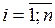 , если
, если 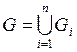 .
.
Разбиение будем обозначать буквой Т, 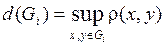 – диаметр множества
– диаметр множества 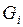 . Число
. Число 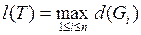 называется мелкостью разбиения.
называется мелкостью разбиения.
Опр. Пусть функция f(x) определена на измеримом по Жордану множестве 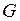 ,
, 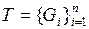 − разбиение множества
− разбиение множества 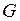 .
.
Возьмем в каждом множестве 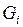 произвольную точку
произвольную точку 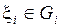 .
.
Выражение 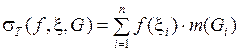 называется интегральной суммой Римана функции f(x) на множестве
называется интегральной суммой Римана функции f(x) на множестве 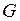 , соответствующей разбиению T и выборке
, соответствующей разбиению T и выборке 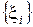 .
.
Опр. Число I называется пределом интегральных сумм 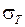 при мелкости разбиения
при мелкости разбиения 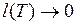 , если
, если 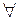
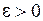
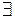
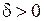 , такое, что для любого разбиения с мелкостью
, такое, что для любого разбиения с мелкостью 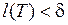 и при любом выборе точек
и при любом выборе точек 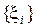 выполняется неравенство
выполняется неравенство
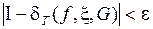 .
.
Если число I является пределом интегральных сумм при 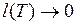 , то число I называют кратным интегралом Римана от функции f(x) по множеству
, то число I называют кратным интегралом Римана от функции f(x) по множеству 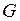 , а функцию f(x) − интегрируемой по множеству
, а функцию f(x) − интегрируемой по множеству 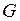 .
.
Обозначается 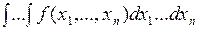 или
или 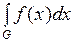
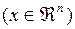 .
.
В случае 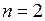 интеграл называется двойным, а в случае
интеграл называется двойным, а в случае 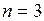 − тройным. Обозначается …
− тройным. Обозначается …
Прежде, чем сформулировать теорему, введем определение.
Если f(x) ограничена на множестве 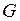 , то для
, то для  разбиения T определены числа
разбиения T определены числа 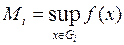 и
и 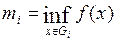 .
.
Выражения 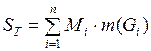 и
и 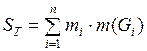 называются соответственно верхней и нижней суммами Дарбу, соответствующими разбиению Т.
называются соответственно верхней и нижней суммами Дарбу, соответствующими разбиению Т.
Теорема (критерий интегрируемости)
Ограниченная функция 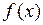 интегрируема по множеству
интегрируема по множеству 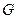 тогда и только тогда, когда
тогда и только тогда, когда 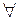
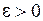
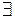
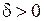 : для любого разбиения с мелкостью
: для любого разбиения с мелкостью 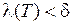 выполняется неравенство
выполняется неравенство 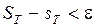 , т.е.
, т.е. 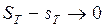 при
при 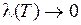 .
.
П.3. Классы интегрируемых функций
Теорема 1 Непрерывная на измеримом по Жордану компакте функция интегрируема на нем.
Теорема 2 Пусть функция 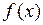 ограничена на измеримом по Жордану компакте
ограничена на измеримом по Жордану компакте 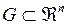 и множество ее точек разрыва имеет Жорданову меру 0, тогда
и множество ее точек разрыва имеет Жорданову меру 0, тогда 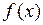 интегрируема на множестве
интегрируема на множестве 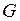 .
.
Доказательство. Пусть Е − множество точек разрыва функции 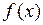 и
и 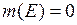 . Тогда
. Тогда 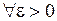 существует открытое клеточное множество А, такое, что
существует открытое клеточное множество А, такое, что 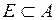 и
и 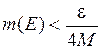 , где
, где 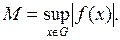
На множестве 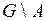 (а оно замкнуто и ограничено)
(а оно замкнуто и ограничено) 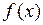 непрерывна, следовательно, интегрируема. Значит,
непрерывна, следовательно, интегрируема. Значит, 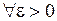 существует разбиение
существует разбиение 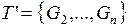 множества
множества 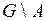 такое, что
такое, что
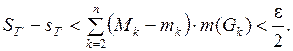
Пусть 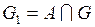 . Тогда множества
. Тогда множества 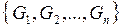 образуют разбиение Т множества
образуют разбиение Т множества 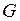 , причем
, причем 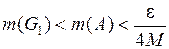 .
.
Тогда 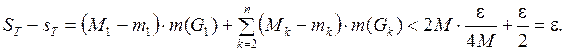
Сведение кратных интегралов к повторным
П.2 Сведение двойного интеграла по элементарной области
К повторному интегралу
Пусть  и
и  − непрерывны на
− непрерывны на 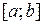 и
и 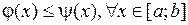 .
.
Область 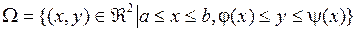 называется элементарной относительно оси
называется элементарной относительно оси 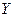 . Это множество является измеримым по Жордану, т.к. ограничено кривыми и отрезками.
. Это множество является измеримым по Жордану, т.к. ограничено кривыми и отрезками.
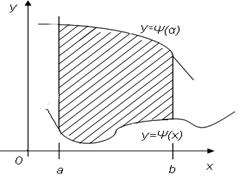
Теорема 2 Пусть  элементарная относительно оси
элементарная относительно оси  область, функция
область, функция  интегрируема на
интегрируема на 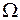 и
и 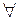
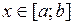
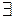
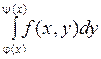 , тогда
, тогда
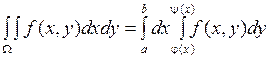 . (2)
. (2)
Следствие Если 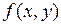 непрерывна на
непрерывна на 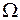 , то справедлива формула (2).
, то справедлива формула (2).
Пример Вычислить 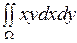 , если
, если 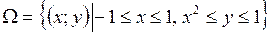 .
.
Опр. Определим область, элементарную относительно оси 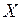 − это множество
− это множество 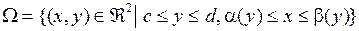 .
.
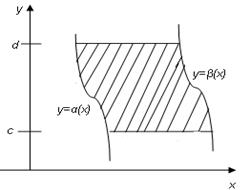
Теорема 3 Если 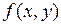 непрерывна в области
непрерывна в области 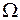 , элементарной относительно оси
, элементарной относительно оси 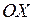 , то
, то 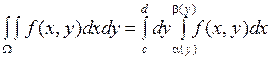 .
.
П.1 Двойные интегралы
Рассмотрим 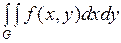 . Перейдем от переменных
. Перейдем от переменных 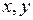 к переменным
к переменным 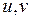 по формулам:
по формулам: 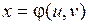 ,
, 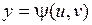 ,
, 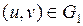 .
.
При этом отображении каждой точке 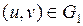 соответствует некоторая точка
соответствует некоторая точка 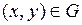 . (Т.е. если точка (
. (Т.е. если точка ( 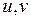 ) пробегает область
) пробегает область 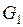 , то (
, то ( 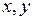 ) пробегает область
) пробегает область 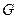 .) Область
.) Область  является образом
является образом 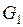 при данном отображении.
при данном отображении.
Пусть отображение 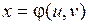 ,
, 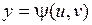 ,
, 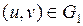 (1) удовлетворяет следующим условиям:
(1) удовлетворяет следующим условиям:
1) Отображение (1) взаимно однозначно (т.е. различные точки области 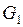 переходят в различные точки области
переходят в различные точки области  );
);
2) Функции 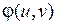 и
и 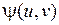 имеют непрерывные частные производные первого порядка в области
имеют непрерывные частные производные первого порядка в области 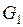 ;
;
3) 
 Якобиан отображения
Якобиан отображения 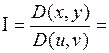
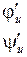
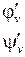 ≠ 0 в
≠ 0 в 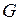 .
.
Теорема Пусть  и
и 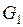 - замкнутые ограниченные множества, функция
- замкнутые ограниченные множества, функция 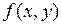 ограничена в области
ограничена в области  и непрерывна всюду, кроме, быть может, некоторого множества меры 0, а отображение (1) удовлетворяет условиям 1-3. Тогда справедливо равенство
и непрерывна всюду, кроме, быть может, некоторого множества меры 0, а отображение (1) удовлетворяет условиям 1-3. Тогда справедливо равенство
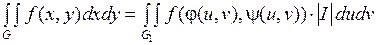 .
.
Замечание 1 Отображение, удовлетворяющее условиям 1-3, обладает следующими свойствами:
1) непрерывные кривые при этом отображении переходят в непрерывные кривые;
2) граница области 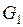 переходит в границу области
переходит в границу области  .
.
Замечание 2
Если условие 1 (взаимная однозначность отображения (1)) или условие 3 (неравенство нулю Якобиана) нарушается на множестве меры 0 (например, в отдельных точках или на отдельных кривых), то формула замены переменных остается в силе.
Пример Вычислить 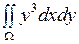 , если
, если 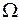 ограничена кривыми:
ограничена кривыми: 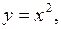
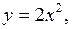
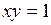 ,
, 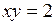 .
.
Решение. Замена 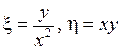 . Тогда
. Тогда 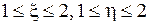 .
.
Выразим 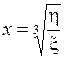 ,
, 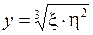 .
.
Якобиан I = 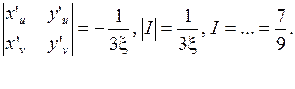
Свойства множеств жордановой меры 0.
1) Множество меры 0 измеримо по Жордану (по определению).
2) Объединение конечного числа множеств меры 0 есть множество меры 0.
3) Подмножество множества меры 0 есть множество меры 0.
Дата: 2019-03-05, просмотров: 528.