Пусть функция 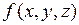 определена в области  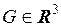и пусть точка 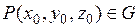. Рассмотрим вектор 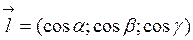, где

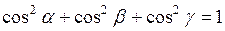, т.е ,  –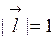

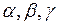углы, которые образует вектор 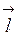 с положительным направлением осей Ox, Oy, Oz соответственно.

O . Производной функции 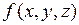 в точке  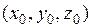  направлении  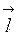называется величина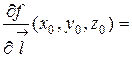

.

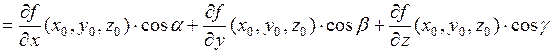Обозначим .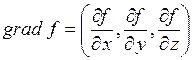

Тогда 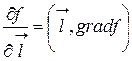 (имеется ввиду скалярное произведение).

Множество точек, для которых 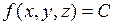, 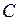= const  будем называть линией уровня функции .

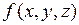Утверждение Вектор 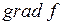 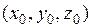ортогонален линии уровня, проходящей через точку 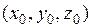. Градиент показывает направление наибольшего роста функции.

П.6 Частные производные и дифференциалы

Высших порядков

Пусть для функции ,  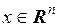существуют частная производная 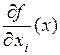. Если эта функция имеет в некоторой точке частную производную 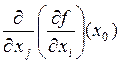, то эта производная называется частной производной второго порядка  и обозначается  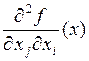или .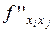

Если 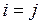, то эта производная обозначается .

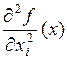Производные  и 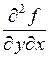 называются смешанными. Вообще говоря, 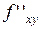не всегда равна .

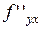Теорема (о смешанных производных) Если обе смешанные производные 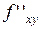 и 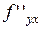 определены в некоторой окрестности точки  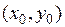и непрерывны в этой точке, то = .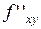

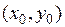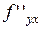
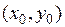Производные более высоких порядков определяются по индукции.

Например, .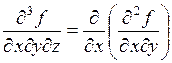

Дифференциалом второго порядка для 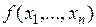 называется величина

.

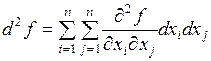Если смешанные производные непрерывны, то для функции 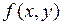 двух переменных .

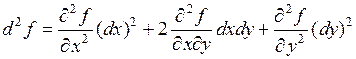Если обозначить оператор 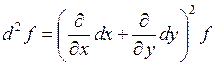, то для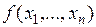

,

.

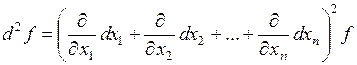Например, .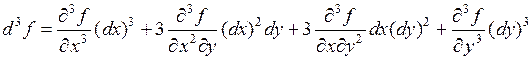

Отметим, что дифференциалы второго и более высокого порядков не обладают свойством инвариантности относительно замены переменных.

П.7 Формула Тейлора для функций

Нескольких переменных

Теорема Если функция 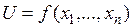 дифференцируема  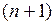раз в некоторой окрестности точки  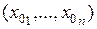(т.е. все частные производные n-го порядка дифференцируемы в этой точке), то для любой точки  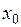из этой окрестности справедливо равенство:

.

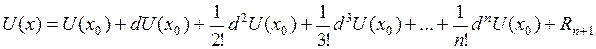Здесь .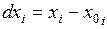

Остаточный член в форме Пеано: 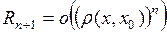, при .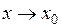

Остаточный член в форме Лагранжа: .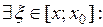

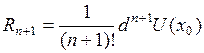§5 Локальный экстремум функции

Нескольких переменных

 п.1 Определения

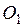. Пусть  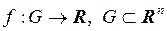и пусть .

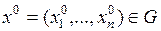Точка 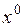 называется точкой (локального) минимума функции , если существует такой шар 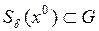, что для  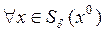выполняется неравенство .

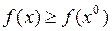Если выполняется неравенств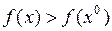о , то 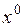 – точка строгого локального минимума функции .

Аналогично определяются точки локального максимума (строгого локального максимума) функции .

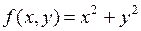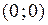Например, для функции  точка  является точкой строгого минимума, т.к. .

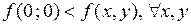. Точки локального максимума и точки локального минимума функции называются точками экстремума.

Теорема 1 Если 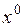 – точка экстремума функции  и существует частная производная 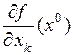, то она равна нулю.

Следствие Если 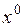 – точка экстремума функции , и  дифферен-цируема в этой точке, то

.

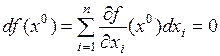Действительно, т.к.  дифференцируема в точке 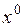, то в этой точке существуют все частные производные, и они равны нулю.

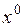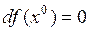. Если  дифференцируема в точке  и , то 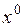 называется стационарной точкой функции  (иногда называют точкой возможного экстремума).

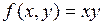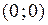Замечание. Точка экстремума дифференцируемой функции всегда является стационарной точкой. Обратное не всегда верно. Например, для  точка  является стационарной точкой, но не является точкой экстремума, так как в любой её окрестности есть точки вида  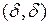такие, что 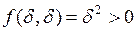, и есть точки вида  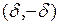такие, что . При этом .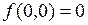

Теорема 2 Пусть 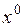 – точка минимума функции , функция  имеет в окрестности точки 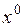 непрерывные частные производные I и II порядка. Тогда 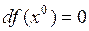, 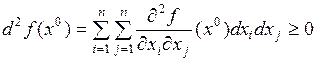. Если же  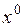– точка максимума функции , то , .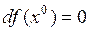

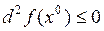Замечание. Условия 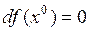 и 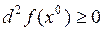 необходимы, но не достаточны для того, чтобы  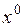была точкой минимума функции . Например, для 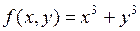 в точке  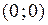выполнено:

, .

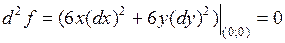Но точка 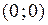 не является точкой экстремума.