П.2 Непрерывность функции многих переменных
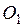 . Функция
. Функция 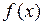 , определенная в некоторой окрестности точки
, определенная в некоторой окрестности точки 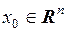 , непрерывна в точке
, непрерывна в точке 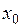 , если существует
, если существует 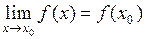 .
.
 . Функция
. Функция 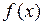 , определенная в окрестности
, определенная в окрестности 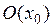 , непрерывна в точке
, непрерывна в точке 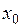 , если
, если 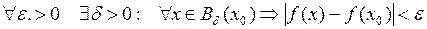 .
.
 . Функция
. Функция 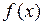 называется непрерывной на множестве М, если она непрерывна в каждой точке этого множества.
называется непрерывной на множестве М, если она непрерывна в каждой точке этого множества.
Пример Функция  не является непрерывной в точке
не является непрерывной в точке 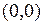 , так как не существует
, так как не существует  . Действительно, если взять две последовательности
. Действительно, если взять две последовательности 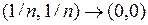 и
и 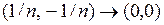 , то получим
, то получим
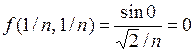 ,
, 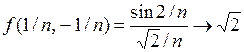 при
при 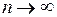 .
.
Теорема (о непрерывности сложной функции) Пусть функции 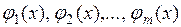 определены в некоторой окрестности точки
определены в некоторой окрестности точки 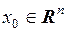 и непрерывны в точке
и непрерывны в точке 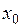 ; функция
; функция  определена в окрестности точки
определена в окрестности точки 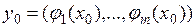 и непрерывна в точке
и непрерывна в точке 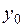 . Тогда в некоторой окрестности точки
. Тогда в некоторой окрестности точки 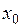 определена сложная функция
определена сложная функция 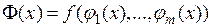 , которая непрерывна в точке
, которая непрерывна в точке 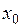 .
.
Пример 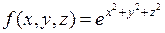 непрерывна на
непрерывна на 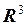 .
.
Здесь 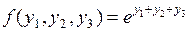 ,
,  ,
, 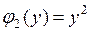 ,
,  .
.
 §3 Дифференцируемость функций многих переменных
§3 Дифференцируемость функций многих переменных
п.1 Частные производные
Пусть функция 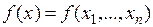 определена в окрестности точки
определена в окрестности точки 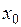 . Зафиксируем переменные
. Зафиксируем переменные 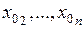 . Тогда функцию
. Тогда функцию 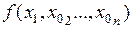 можно рассматривать как функцию одной переменной
можно рассматривать как функцию одной переменной 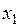 . Если такая функция имеет производную, то эта производная называется частной производной функции
. Если такая функция имеет производную, то эта производная называется частной производной функции 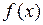 по переменной
по переменной 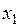 . Таким образом,
. Таким образом,
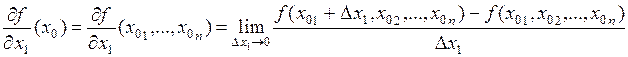 .
.
Аналогично, при 
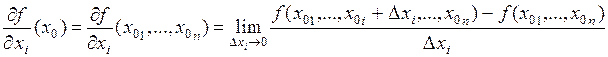 .
.
Обозначается i -тая частная производная также 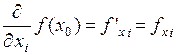 .
.
Так как при вычислении частных производных все переменные, кроме одной, фиксируются, то техника вычисления частных производных такая же, как техника вычисления производных функций одной переменной. Например, если 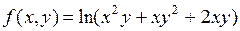 , то
, то 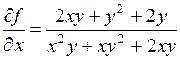 ,
,  .
.
П.2 Дифференцируемость функций многих переменных
О. Функция 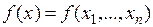 называется дифференцируемой в точке
называется дифференцируемой в точке  , если она определена в некоторой окрестности
, если она определена в некоторой окрестности 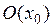 и существуют такие числа
и существуют такие числа  , что приращение функции
, что приращение функции 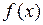 в точке
в точке 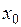 представимо в виде:
представимо в виде:
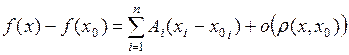 при
при 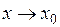 .
.
Теорема Если функция 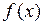 дифференцируема в точке
дифференцируема в точке 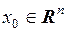 , то она имеет все частные производные
, то она имеет все частные производные 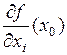 ,
,  , причем
, причем
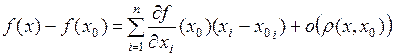 при
при 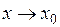 .
.
Доказательство. Пусть функция 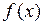 дифференцируема в точке
дифференцируема в точке 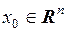 . Это значит, что существуют такие числа
. Это значит, что существуют такие числа  , что при
, что при 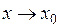
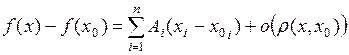 .
.
Возьмем в последнем равенстве 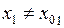 ,
, 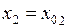 , … ,
, … , 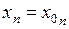 .
.
Тогда последнее равенство примет вид:
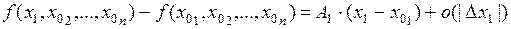 ,
, 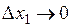 .
.
Разделим это равенство на 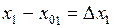 и устремим
и устремим 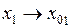 . Получим
. Получим
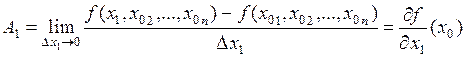 .
.
Аналогично доказывается, что 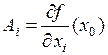 ,
,  ■
■
Доказанная теорема говорит о том, что дифференцируемость функции является достаточным условием для существования частных производных. Однако существование частных производных в точке не достаточно для дифференцируемости функции в точке.
Теорема Если все частные производные 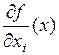 ,
,  определены в окрестности точки
определены в окрестности точки 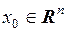 и непрерывны в точке
и непрерывны в точке 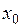 , то функция
, то функция 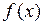 дифференцируема в точке
дифференцируема в точке 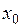 .
.
Непрерывность частных производных в точке является достаточным условием дифференцируемости функции, но не является необходимым условием.
Дифференциала
Пусть функция  дифференцируема на открытом множестве
дифференцируема на открытом множестве 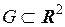 . Рассмотрим её график, т.е. множество
. Рассмотрим её график, т.е. множество
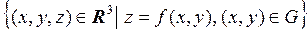 .
.
Пусть точка 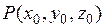 лежит на графике функции
лежит на графике функции 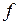 , т.е.
, т.е. 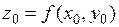 .
.
Найдем дифференциал  .
.
Известно, что вектор 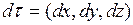 есть касательный вектор к кривой Г, проходящей через точку
есть касательный вектор к кривой Г, проходящей через точку 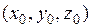 и лежащей на графике функции
и лежащей на графике функции 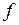 .
.
Условие 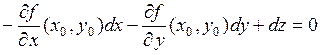 означает, что вектор
означает, что вектор 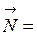
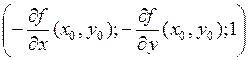 ортогонален вектору касательной. Поэтому вектор
ортогонален вектору касательной. Поэтому вектор 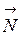 ортогонален любой кривой, лежащей на графике
ортогонален любой кривой, лежащей на графике 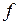 и проходящей через точку
и проходящей через точку 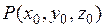 . Его называют вектором нормали к графику функций в точке Р.
. Его называют вектором нормали к графику функций в точке Р.
Плоскость, проходящая через точку Р и ортогональная вектору нормали 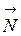 , называется касательной плоскостью к графику функции
, называется касательной плоскостью к графику функции 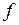 в точке Р. Её уравнение имеет вид:
в точке Р. Её уравнение имеет вид:
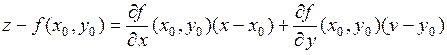 .
.
Прямая, проходящая через точку Р и перпендикулярная касательной плоскости, называется нормалью к графику функции 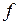 в точке Р. Её уравнение имеет вид:
в точке Р. Её уравнение имеет вид:
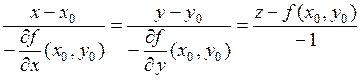 .
.
Если поверхность задана неявно, т.е. уравнением 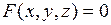 , то уравнение касательной плоскости имеет вид:
, то уравнение касательной плоскости имеет вид:
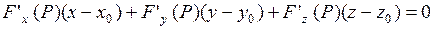 .
.
Из уравнения касательной плоскости получаем:
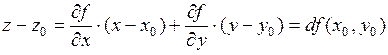 .
.
Получили геометрический смысл дифференциала: 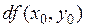 есть приращение аппликаты (координаты z) на касательной плоскости.
есть приращение аппликаты (координаты z) на касательной плоскости.
Геометрический смысл дифференцируемости функции в точке: если функция  дифференцируема в точке
дифференцируема в точке 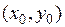 , то в точке
, то в точке 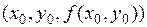 существует касательная плоскость к графику этой функции.
существует касательная плоскость к графику этой функции.
Высших порядков
Пусть для функции  ,
, 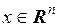 существуют частная производная
существуют частная производная 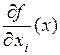 . Если эта функция имеет в некоторой точке частную производную
. Если эта функция имеет в некоторой точке частную производную 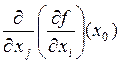 , то эта производная называется частной производной второго порядка и обозначается
, то эта производная называется частной производной второго порядка и обозначается 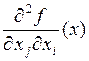 или
или 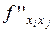 .
.
Если 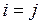 , то эта производная обозначается
, то эта производная обозначается 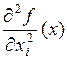 .
.
Производные  и
и 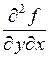 называются смешанными. Вообще говоря,
называются смешанными. Вообще говоря, 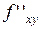 не всегда равна
не всегда равна 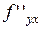 .
.
Теорема (о смешанных производных) Если обе смешанные производные 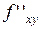 и
и 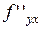 определены в некоторой окрестности точки
определены в некоторой окрестности точки 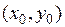 и непрерывны в этой точке, то
и непрерывны в этой точке, то 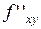
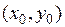 =
= 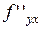
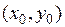 .
.
Производные более высоких порядков определяются по индукции.
Например, 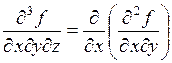 .
.
Дифференциалом второго порядка для  называется величина
называется величина
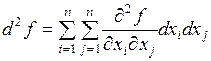 .
.
Если смешанные производные непрерывны, то для функции 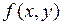 двух переменных
двух переменных 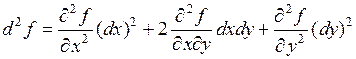 .
.
Если обозначить оператор 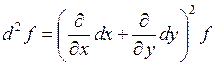 , то для
, то для 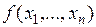
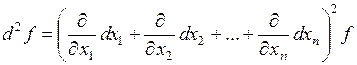 ,
,
 .
.
Например, 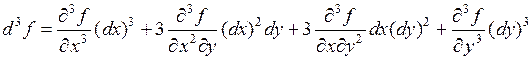 .
.
Отметим, что дифференциалы второго и более высокого порядков не обладают свойством инвариантности относительно замены переменных.
Нескольких переменных
Теорема Если функция 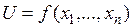 дифференцируема
дифференцируема 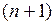 раз в некоторой окрестности точки
раз в некоторой окрестности точки 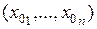 (т.е. все частные производные n-го порядка дифференцируемы в этой точке), то для любой точки
(т.е. все частные производные n-го порядка дифференцируемы в этой точке), то для любой точки 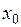 из этой окрестности справедливо равенство:
из этой окрестности справедливо равенство:
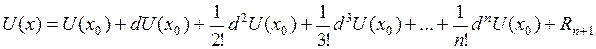 .
.
Здесь 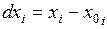 .
.
Остаточный член в форме Пеано: 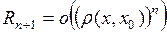 , при
, при 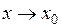 .
.
Остаточный член в форме Лагранжа: 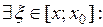
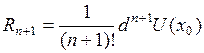 .
.
 §5 Локальный экстремум функции
§5 Локальный экстремум функции
Нескольких переменных
п.1 Определения
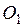 . Пусть
. Пусть 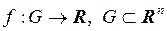 и пусть
и пусть 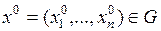 .
.
Точка 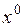 называется точкой (локального) минимума функции
называется точкой (локального) минимума функции  , если существует такой шар
, если существует такой шар 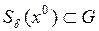 , что для
, что для 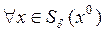 выполняется неравенство
выполняется неравенство 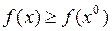 .
.
Если выполняется неравенство 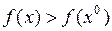 , то
, то 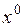 – точка строгого локального минимума функции
– точка строгого локального минимума функции  .
.
Аналогично определяются точки локального максимума (строгого локального максимума) функции  .
.
Например, для функции 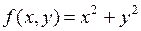 точка
точка 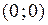 является точкой строгого минимума, т.к.
является точкой строгого минимума, т.к. 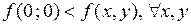 .
.
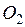 . Точки локального максимума и точки локального минимума функции называются точками экстремума.
. Точки локального максимума и точки локального минимума функции называются точками экстремума.
Теорема 1 Если 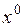 – точка экстремума функции
– точка экстремума функции  и существует частная производная
и существует частная производная 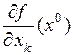 , то она равна нулю.
, то она равна нулю.
Следствие Если 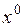 – точка экстремума функции
– точка экстремума функции  , и
, и  дифферен-цируема в этой точке, то
дифферен-цируема в этой точке, то
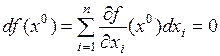 .
.
Действительно, т.к.  дифференцируема в точке
дифференцируема в точке 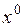 , то в этой точке существуют все частные производные, и они равны нулю.
, то в этой точке существуют все частные производные, и они равны нулю.
 . Если
. Если  дифференцируема в точке
дифференцируема в точке 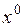 и
и 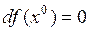 , то
, то 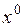 называется стационарной точкой функции
называется стационарной точкой функции  (иногда называют точкой возможного экстремума).
(иногда называют точкой возможного экстремума).
Замечание. Точка экстремума дифференцируемой функции всегда является стационарной точкой. Обратное не всегда верно. Например, для 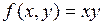 точка
точка 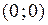 является стационарной точкой, но не является точкой экстремума, так как в любой её окрестности есть точки вида
является стационарной точкой, но не является точкой экстремума, так как в любой её окрестности есть точки вида 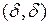 такие, что
такие, что 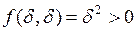 , и есть точки вида
, и есть точки вида 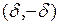 такие, что
такие, что  . При этом
. При этом 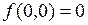 .
.
Теорема 2 Пусть 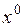 – точка минимума функции
– точка минимума функции  , функция
, функция  имеет в окрестности точки
имеет в окрестности точки 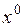 непрерывные частные производные I и II порядка. Тогда
непрерывные частные производные I и II порядка. Тогда 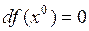 ,
, 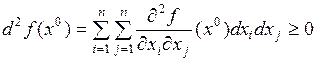 . Если же
. Если же 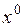 – точка максимума функции
– точка максимума функции  , то
, то 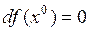 ,
, 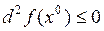 .
.
Замечание. Условия 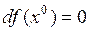 и
и 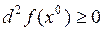 необходимы, но не достаточны для того, чтобы
необходимы, но не достаточны для того, чтобы 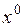 была точкой минимума функции
была точкой минимума функции  . Например, для
. Например, для 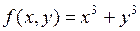 в точке
в точке 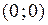 выполнено:
выполнено:
 ,
, 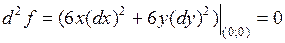 .
.
Но точка 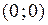 не является точкой экстремума.
не является точкой экстремума.
п.2 Непрерывность функции многих переменных
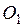 . Функция
. Функция 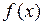 , определенная в некоторой окрестности точки
, определенная в некоторой окрестности точки 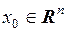 , непрерывна в точке
, непрерывна в точке 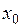 , если существует
, если существует 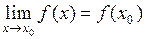 .
.
 . Функция
. Функция 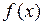 , определенная в окрестности
, определенная в окрестности 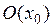 , непрерывна в точке
, непрерывна в точке 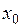 , если
, если 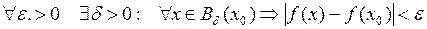 .
.
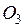 . Функция
. Функция 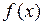 называется непрерывной на множестве М, если она непрерывна в каждой точке этого множества.
называется непрерывной на множестве М, если она непрерывна в каждой точке этого множества.
Пример Функция  не является непрерывной в точке
не является непрерывной в точке 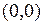 , так как не существует
, так как не существует  . Действительно, если взять две последовательности
. Действительно, если взять две последовательности 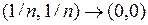 и
и 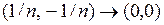 , то получим
, то получим
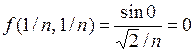 ,
, 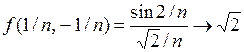 при
при 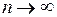 .
.
Теорема (о непрерывности сложной функции) Пусть функции 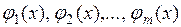 определены в некоторой окрестности точки
определены в некоторой окрестности точки 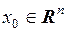 и непрерывны в точке
и непрерывны в точке 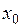 ; функция
; функция  определена в окрестности точки
определена в окрестности точки 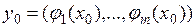 и непрерывна в точке
и непрерывна в точке 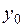 . Тогда в некоторой окрестности точки
. Тогда в некоторой окрестности точки 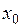 определена сложная функция
определена сложная функция 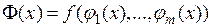 , которая непрерывна в точке
, которая непрерывна в точке 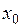 .
.
Пример 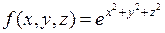 непрерывна на
непрерывна на 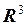 .
.
Здесь 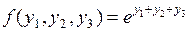 ,
,  ,
, 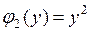 ,
,  .
.
 §3 Дифференцируемость функций многих переменных
§3 Дифференцируемость функций многих переменных
п.1 Частные производные
Пусть функция 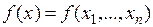 определена в окрестности точки
определена в окрестности точки 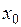 . Зафиксируем переменные
. Зафиксируем переменные 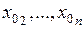 . Тогда функцию
. Тогда функцию 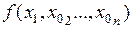 можно рассматривать как функцию одной переменной
можно рассматривать как функцию одной переменной 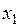 . Если такая функция имеет производную, то эта производная называется частной производной функции
. Если такая функция имеет производную, то эта производная называется частной производной функции 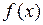 по переменной
по переменной 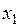 . Таким образом,
. Таким образом,
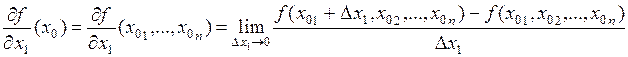 .
.
Аналогично, при 
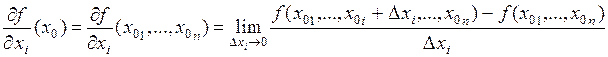 .
.
Обозначается i -тая частная производная также 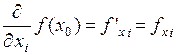 .
.
Так как при вычислении частных производных все переменные, кроме одной, фиксируются, то техника вычисления частных производных такая же, как техника вычисления производных функций одной переменной. Например, если 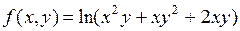 , то
, то 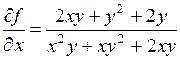 ,
,  .
.
Дата: 2019-03-05, просмотров: 318.