О. Функция 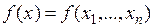 называется дифференцируемой в точке 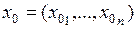, если она определена в некоторой окрестности  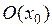и существуют такие числа 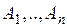, что приращение функции 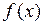в точке  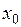представимо в виде:

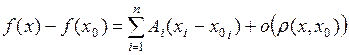 при .

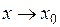Теорема Если функция 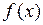 дифференцируема в точке 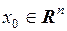, то она имеет все частные производные 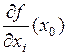, , 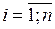причем

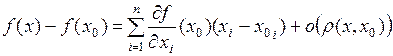 при .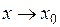

Доказательство. Пусть функция 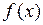 дифференцируема в точке 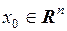. Это значит, что существуют такие числа 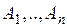, что при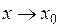

.

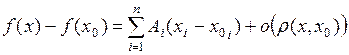Возьмем в последнем равенстве , , … , .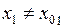

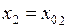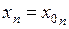Тогда последнее равенство примет вид:

, .

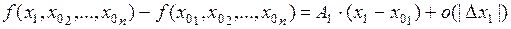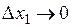Разделим это равенство на 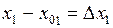 и устремим 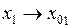. Получим

.

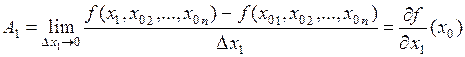Аналогично доказывается, что , ■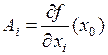

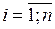Доказанная теорема говорит о том, что дифференцируемость функции является достаточным условием для существования частных производных. Однако существование частных производных в точке не достаточно для дифференцируемости функции в точке.

Теорема Если все частные производные 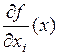,  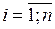определены в окрестности точки  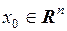и непрерывны в точке 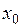, то функция  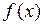дифференцируема в точке .

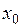Непрерывность частных производных в точке является достаточным условием дифференцируемости функции, но не является необходимым условием.

П.3 Дифференциал функции многих переменных

Пусть 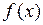 дифференцируема в точке 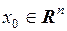. Тогда при  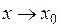её приращение представимо в виде:

, .

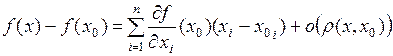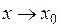Обозначим .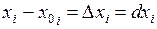

О. Если функция 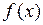 дифференцируема в точке 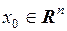, то линейную (относительно приращений 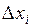) часть приращения функции называют дифференциалом функции  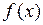в точке  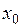 и обозначают 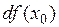, т.е.

.

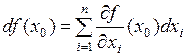Тогда 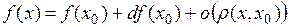 при .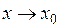

П. 4 Касательная плоскость к графику

 функции двух переменных. Геометрический смысл

Дифференциала

Пусть функция 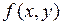 дифференцируема на открытом множестве 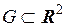. Рассмотрим её график, т.е. множество

.

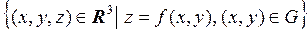Пусть точка 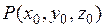 лежит на графике функции 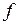, т.е. .

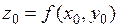Найдем дифференциал .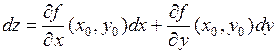

Известно, что вектор 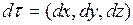 есть касательный вектор к кривой Г, проходящей через точку  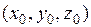и лежащей на графике функции .

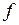Условие 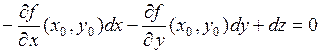 означает, что вектор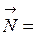 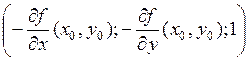 ортогонален вектору касательной. Поэтому вектор  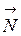ортогонален любой кривой, лежащей на графике  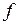и проходящей через точку 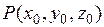. Его называют вектором нормали к графику функций в точке Р.

Плоскость, проходящая через точку Р и ортогональная вектору нормали 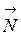, называется касательной плоскостью к графику функции  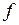в точке Р. Её уравнение имеет вид:

.

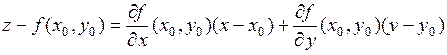Прямая, проходящая через точку Р и перпендикулярная касательной плоскости, называется нормалью к графику функции 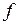 в точке Р. Её уравнение имеет вид:

.

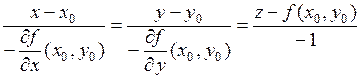Если поверхность задана неявно, т.е. уравнением 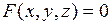, то уравнение касательной плоскости имеет вид:

.

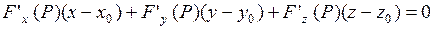Из уравнения касательной плоскости получаем:

.

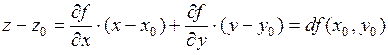Получили геометрический смысл дифференциала: 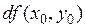 есть приращение аппликаты (координаты z)  на касательной плоскости.

Геометрический смысл дифференцируемости функции в точке: если функция 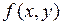 дифференцируема в точке 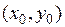, то в точке  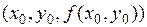существует касательная плоскость к графику этой функции.