Метод трапеций является одним из методов численного интегрирования. Он позволяет вычислять определенные интегралы с заранее заданной степенью точности.
Опишем суть метода трапеций и выведем формулу трапеций. Далее запишем оценку абсолютной погрешности метода.
Пусть функция 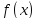 непрерывна на отрезке [a, b], заменим её многочленом Лагранжа первой степени с узлами
непрерывна на отрезке [a, b], заменим её многочленом Лагранжа первой степени с узлами 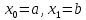 . Это соответствует замене кривой на секущую. Искомый интеграл, равный площади криволинейной фигуры, заменяется на площадь трапеции (рис. 10).
. Это соответствует замене кривой на секущую. Искомый интеграл, равный площади криволинейной фигуры, заменяется на площадь трапеции (рис. 10).
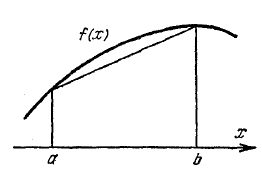
Рис. 10 Геометрическая интерпретация метода трапеций
Из геометрических соображений нетрудно написать для него формулу трапеций
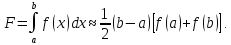 (1)
(1)
Это одна из простейших квадратурных формул. Найдем её погрешность. Для этого разложим 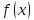 по формуле Тейлора, выбирая середину отрезка за центр разложения и предполагая наличие у функции требуемых непрерывных производных:
по формуле Тейлора, выбирая середину отрезка за центр разложения и предполагая наличие у функции требуемых непрерывных производных:
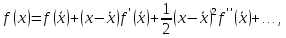
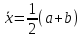 (2)
(2)
Погрешность есть разность точного и приближенного значений интеграла. Подставляя в (1) разложение (2), получим главный член погрешности
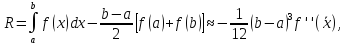 (3)
(3)
где члены, отброшенные при замене точного равенства приближенным, содержат старшие производные и более высокие степени длины отрезка интегрирования. Заметим, что содержащие 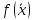 и
и 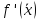 члены разложения (2) уничтожились и не дали вклада в погрешность; это нетрудно было предвидеть, ибо формула трапеций по самому выводу точна для многочлена первой степени.
члены разложения (2) уничтожились и не дали вклада в погрешность; это нетрудно было предвидеть, ибо формула трапеций по самому выводу точна для многочлена первой степени.
Вообще говоря, длина отрезка b - a не мала, поэтому остаточный член (3) может быть велик. Для повышения точности на отрезке [a, b] вводят достаточно густую сетку 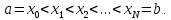 Интеграл разбивают на сумму интегралов по шагам сетки и к каждому шагу применяют формулу (1). Получают обобщенную формулу трапеций
Интеграл разбивают на сумму интегралов по шагам сетки и к каждому шагу применяют формулу (1). Получают обобщенную формулу трапеций
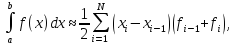
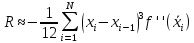 (4)
(4)
На равномерной сетке она упрощается:
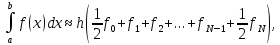
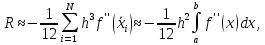 (5)
(5)
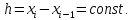
Поскольку в оценке (3) были отброшены члены, содержащие более высокие степени длины интервала, то выражение остаточного члена (5) является асимптотическим, т.е. выполняющимся при 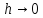 с точностью до членов более высокого порядка малости. Но для справедливости этой оценки необходимо существование непрерывной
с точностью до членов более высокого порядка малости. Но для справедливости этой оценки необходимо существование непрерывной 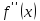 ; если
; если 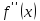 кусочно-непрерывна, то удается сделать лишь мажорантную оценку
кусочно-непрерывна, то удается сделать лишь мажорантную оценку
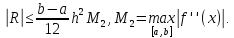 (6)
(6)
Таким образом, обобщенная формула трапеций имеет второй порядок точности относительно шага сетки. На равномерной сетке это видно непосредственно, а на квазиравномерной сетке, порожденной преобразованием 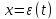 , остаточный член (3) можно привести к виду
, остаточный член (3) можно привести к виду
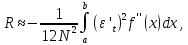 (7)
(7)
если используемые в этой формуле производные непрерывны. Для произвольной неравномерной сетке асимптотическая оценка в виде суммы (6) справедлива, но неудобна для использования; можно пользоваться мажорантной оценкой (7), подразумевая под шагом 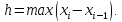
Дата: 2019-03-05, просмотров: 391.