Тригонометрическая система состоит из функций:

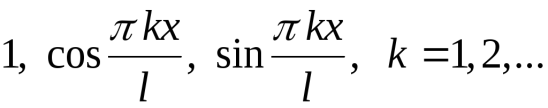(1)

Тригонометрическая система функций является ортогональной в пространстве 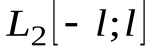, но не является нормированной. В самом деле, легко проверить, что

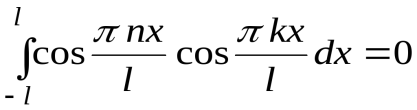при ;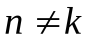

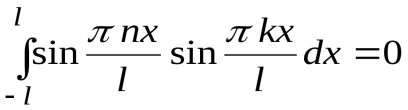
при ;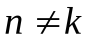

; ; ;

; ; .

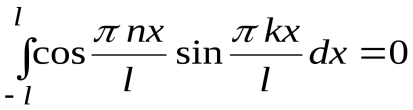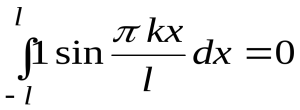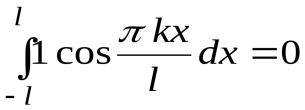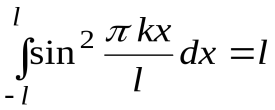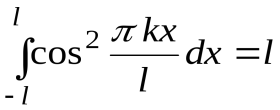Кроме того, тригонометрическая система функций является замкнутой в пространстве .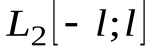

Ряд Фурье по тригонометрической системе принято записывать в виде:

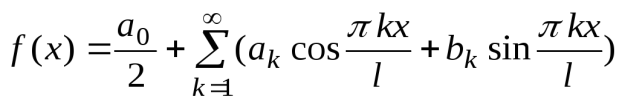, (2)

а коэффициенты ряда вычисляются по формулам:

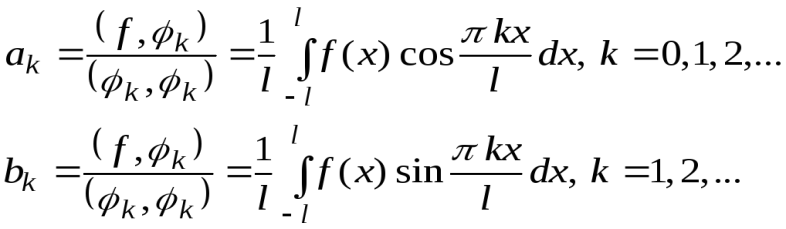(3)

Таким образом, наилучшим среднеквадратическим приближением функции 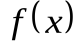в семействе тригонометрических многочленов вида

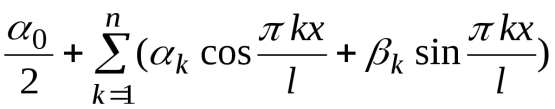(4)

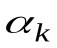(здесь и 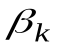- произвольные вещественные постоянные коэффициенты) является частичная сумма тригонометрического ряда Фурье

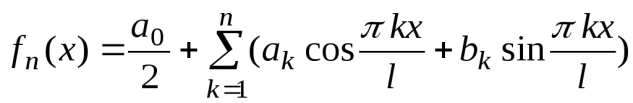. (5)

Из замкнутости тригонометрической системы следует, что погрешность этих приближений, 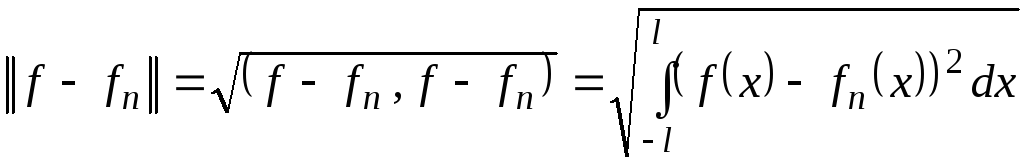стремится к нулю при .

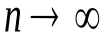Рассмотрим некоторые свойства полученных приближений функции 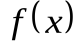тригонометрическими многочленами. Сходимость ряда (1) к функции 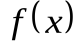по норме пространства 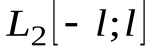не означает, что ряд (1) будет сходиться к функции 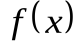в каждой точке отрезка 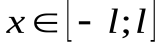. Приведем без доказательства условия поточечной сходимости ряда Фурье к порождающей его функции .

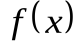Теорема 2. Если функция 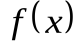кусочно-непрерывна на отрезке 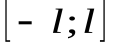и периодична с периодом 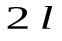, то во всех точках x, где функция 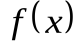непрерывна, сумма ряда Фурье (1) будет совпадать с функцией 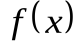. В тех точках, где функция 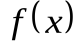терпит разрыв первого рода, сумма ряда Фурье (1) будет равна .

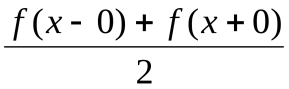В проколотой окрестности точек разрыва первого рода функции 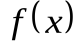-сходимость частичных сумм тригонометрического ряда Фурье 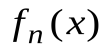к функци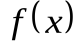и при 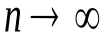является неравномерной. Если, например, функция 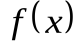имеет период 2 и на периоде задана формулой:

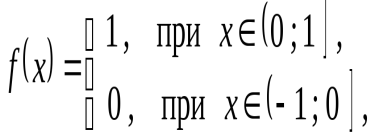
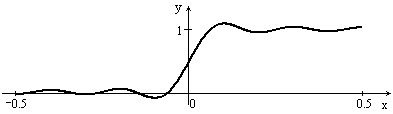
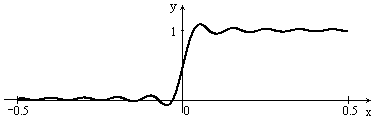
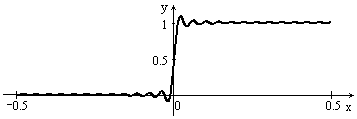
Рис. 7 Приближение при n=10,20,50

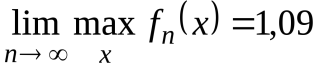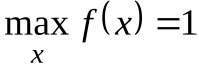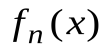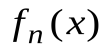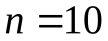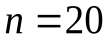то , в то время как (явление Гиббса). Чтобы понять это явление полезно посмотреть, как ведут себя графики частичных сумм тригонометрического ряда Фурье для этого случая с ростом n. На рисунке изображены графики при , и 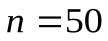(сверху вниз). Из рисунка видно, что в проколотой окрестности точки разрыва ( 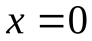) на графиках возникают гребни и провалы, высота которых с ростом n не стремится к нулю (а стремится к 0,09). Эти гребни и провалы с ростом n сужаются и смещаются к точке разрыва. Поэтому при любом фиксированном значении n существуют точки x в окрестности точки разрыва, в которых функция 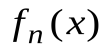отличается от 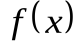на величину, не меньшую 0,09. В самой же точке разрыва 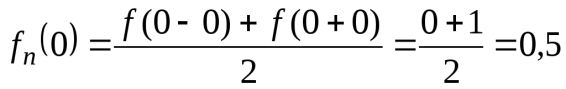при любом n, в то время как .

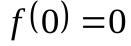Осталось заметить, что если функция 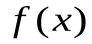является четной, то все интегралы (5.1.26) с синусами обратятся в 0 (как интегралы от нечетных функций с симметричными пределами интегрирования) и ряд Фурье примет вид

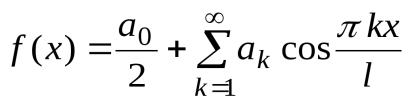. (6)

В этом случае говорят, что функция 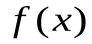разлагается по косинусам.

А если функция 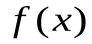является нечетной, то все интегралы (2) с косинусами обратятся в 0 (как интегралы от нечетных функций с симметричными пределами интегрирования) и ряд Фурье примет вид

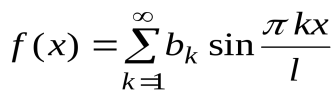. (7)

В этом случае говорят, что функция 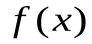разлагается по синусам.