Решение систем нелинейных алгебраических уравнений . 19
Постановка задачи нахождения корней системы из двух нелинейных уравнений . 19
Описание метода секущих . 19
Метод Ньютона как предшественник . 20
Метод простой итерации . 23
Программная реализация метода, решение тестовой задачи . 26
Сравнение полученного результата . 27
4. Решение проблемы собственных значений для матрицы.. 28
4.1. Постановка задачи. 28
4.2. Описание метода QR-алгоритм (Френсис, Кублановская В.Н.) 28
4.3. Программная реализация метода, решение тестовой задачи. 30
4.4. Сравнение полученного результата. 32
5. Интерполирование функции одной переменной. 34
5.1. Постановка задачи. 34
5.2. Описание метода дробно-рационального интерполирования. 34
5.3. Программная реализация метода, решение тестовой задачи. 35
5.4. Сравнение полученного результата. 36
6. Наилучшее приближение функции одной переменной. 38
6.1. Постановка задачи. 38
6.2. Описание метода наилучшего среднеквадратического приближения частичными суммами ряда Фурье. 38
6.3. Программная реализация метода, решение тестовой задачи. 41
6.4. Сравнение полученного результата. 44
7.Численное интегрирование функций. 45
7.1.Потсановка задачи. 45
7.2. Описание метода численного интегрирования методом трапеций. 45
7.3. Программная реализация метода, решение тестовой задачи. 47
7.4. Сравнение полученного результата. 49
Список литературы.. 50
Введение
Цель курсовой работы:
· Изучить и продемонстрировать принцип работы методов решения различных задач численного анализа, в том числе метода секущих для решения системы нелинейных алгебраических уравнений в среде Wolfram Mathematica.
Задачи курсовой:
· познакомиться с несколькими методами решения задач численного анализа;
· описать постановки решаемых задач и алгоритмы реализации используемых методов;
· выполнить программную реализацию методов в среде Wolfram Mathematica;
· решить тестовые задачи и сравнить полученные результаты с точными или с результатами, полученными с использованием встроенных функций.
1. Решение системы линейных уравнений/обращение матрицы (прямой метод)
Постановка задачи
Будем решать матричное уравнение А x = B, в котором А - симметричная матрица, следовательно мы будем искать обратную матрицу численным методом квадратных корней (Метод Холецкого).
Исходные данные:
Сравнение полученного результата
Мы использовали встроенную функцию и видим, что погрешности численного метода относительно точного практически нулевая (погрешность ~0.001).
2. Решение системы линейных уравнений (итерационный метод)
Постановка задачи
Решаем систему линейных уравнений с помощью итерационного метода сопряженных градиентов.
Исходные данные:
Матрица А и вектор начального приближения.
Описание метода секущих
Для уточнения корней систем нелинейных уравнений наиболее часто используют методы итерации (метод простой итерации и метод Зейделя) и метод Ньютона. Как и в случае уточнения корней одного нелинейного уравнения, для систем нелинейных уравнений требуется определение хорошего начального приближения (отделение корня), гарантирующего сходимость метода и высокую скорость ходимости. Для системы двух уравнений это может быть сделано графически, но для систем высоких порядков удовлетворительных методов отделения корней не существует.
В методе секущих, иначе называемом МЕТОДЕ ХОРД, приближенное значение производной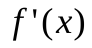 
в формуле определяется по двум последовательным приближениям 
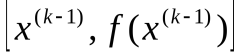и 
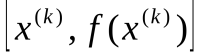по соотношению
что приводит к замене касательной в точке 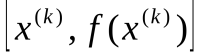секущей, проведенной через две точки кривой y = f(x) (рис.1) или, что то же самое, - к аппроксимации функции f(x) на этом интервале линейной функцией.
Условия сходимости метода секущих аналогичны условиям сходимости метода Ньютона. Порядок сходимости метода секущих определяется соотношениями
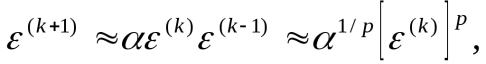
где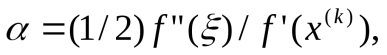 
.
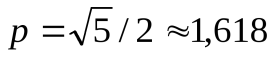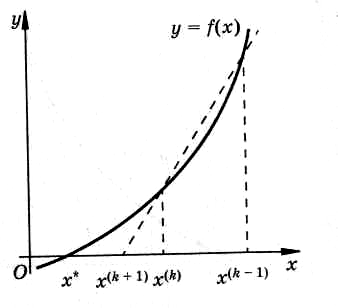Рис.1
Рисунок 1 – Геометрическая интерпретация метода секущих
Метод простой итерации
При использовании метода простой итерации для уточнения корня уравнение f(x) = 0 заменяется эквивалентным уравнением
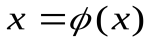(3)
Это означает, что из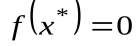 
следует 
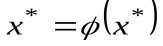и наоборот. Привести уравнение (3) к простому уравнению можно многими способами, например, положив 
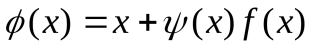, где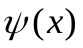 
- непрерывная произвольная знакопостоянная функция.
Геометрически на интервале отделения корня уравнение (3) представляется в виде двух пересекающихся линий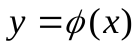 
и y = x (рис. 4). Пологая, что известно начальное приближение 
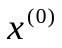для значения корня 
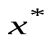, построим итерационный процесс
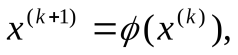k = 0, 1, 2, …, (3.1)
изображенный на рис.4 ломаной линией со стрелочками, указывающими направление движения. Для представленного на рис.4 случая взаимного расположения линий y = x и 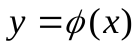неограниченное повторение вычислений по соотношению (3.1) позволяет сколь угодно близко подойти к точному значению корня .
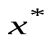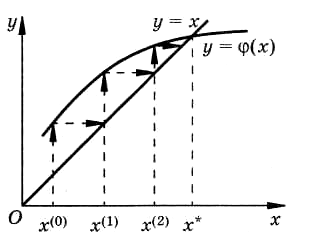
Рисунок 4 – Геометрическая интерпретация метода простой итерации
Исследуем сходимость метода. Если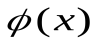 
имеет непрерывную производную, то из теоремы Лагранжа о конечном приращении
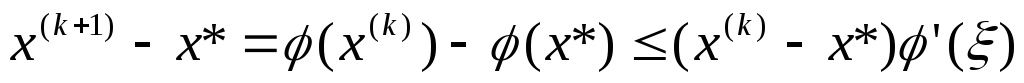(3.2)
следует, что точка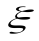 
лежит между точкам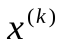и 
и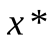 
. Поэтому если всюду 
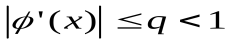, то отрезки 
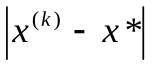убывают не медленнее геометрической прогрессии со знаменателем q<1. Действительно, из (3.2), которое можно рассматривать как рекуррентное соотношение, следует, что 
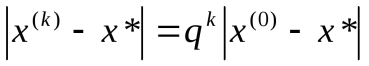и последовательность 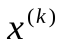сходится при любом нулевом приближении.
Итак, условие:
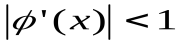(3.3)
Является достаточным условием сходимости итераций. Если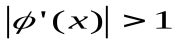 
, то итерации могут не сходиться. Если 
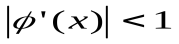, но вдали от корня 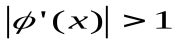, то итерации сходятся, если начальное приближение выбрано достаточно близко к корню. При произвольном начальном приближении сходимости может не быть. Таким образом, в методе простой итерации важен выбор начального приближения. Из соотношения (3.4) следует, что если на интервале отделения корня выполняется условие
,
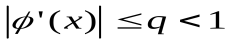то погрешность на каждой итерации уменьшается для любого начального приближения не медленнее членов геометрической прогрессии со знаменателем q.
Четыре случая взаимного расположения линий y = x и 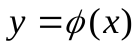вблизи корня и соответствующие им итерационные процессы показаны на рис. 5,a и 5. б соответствуют случаю 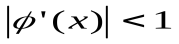– процесс итераций сходится. При этом в первом случае 
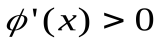и сходимость носит односторонний характер (рис. 5,а), а во втором 
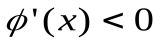и сходимость носит двусторонний характер (рис. 5,б). Рис. 5, в и 5, г соответствуют случаю 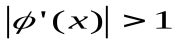– процесс итерации расходится, при этом имеет место односторонняя и двусторонняя расходимость.
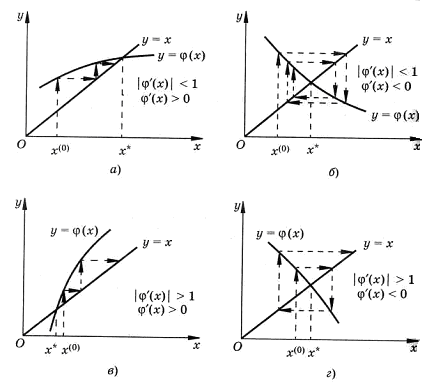
Рисунок 5 – Типовые случаи устойчивой и неустойчивой реализации метода простой итерации
Подчеркнем, что условие (3.3) сходимости метода итераций является лишь достаточным. При этом все приближения должны попадать в отрезок отделения корня. Выполнение условия (3.3) гарантирует сходимость процесса (3.1), но невыполнение условия (3.3) в общем случае не означает, что итерационный процесс окажется расходящимся. Например, для случая, проиллюстрированного рис.6, условие (3.3) на интервале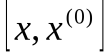 
не выполняется, но метод итераций сходится.
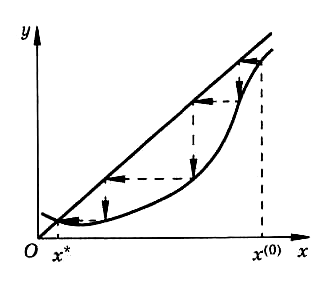
Рисунок 6 – Частный случай сходимости метода простой итерации
Используя соотношения(3.2) и (3.3), можно записать
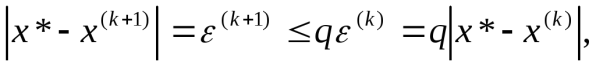
где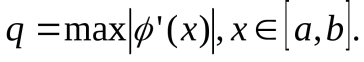 
Из этого соотношения следует, что скорость сходимости метода итерации зависит от величины q: чем меньше q, тем быстрее сходится метод.
Исходное уравнение f(x) = 0 может быть преобразовано к виду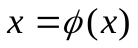 
многими способами, и, очевидно, для метода итерации целесообразно брать то уравнение 
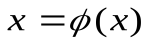, для которого q имеет наименьшее значение.
Для пояснения рассмотрим классический пример вычисления квадратного корня. Исходное уравнение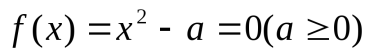 
преобразуем к виду 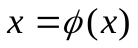тремя способами, приведенными в табл. 1 в первом столбце.
Анализ поведения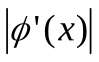 
вблизи корня (третий столбец таблицы) показывает, что при удачном выборе представления 
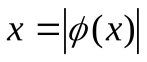можно обеспечить высокую скорость сходимости итерационного процесса без ограничения диапазона параметра а. Третье уравнение 
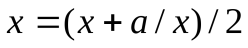используется для вычисления квадратного корня на компьютерах. Таким образом, в методе простой итерации важен выбор вида функций 
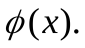Отметим, что метод простой итерации обобщается на случай систем линейных уравнений.
Постановка задачи
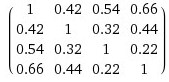
Будем искать собственные значения симметричной, положительно-определенной матрицы с помощью классического QR-алгоритма.
Исходные данные:
1, 0.42, 0.54, 0.66
0.42, 1, 0.32, 0.44
0.54, 0.32, 1, 022
0.66, 0.44, 0.22, 1
Постановка задачи
Будем интерполировать функцию Log(x) дробно-рациональным методом. В качестве узлов x возьмем значения 1,2,3,4,5.
Постановка задачи
Возьмем функцию x2*Sin[x], разложим ее в ряд Фурье и с помощью встроенной функции в Wolfram построим исходный график функции и апроскимированный частичными суммами ряда (их будет 3). Будем исследовать наилучшее приближение тригонометрическими суммами.
Потсановка задачи
Будем интегрировать функцию (брать определенный интеграл) приближенным методом трапеций.
Исходный данные: ∫7/(x^2+1) на промежутке от 0 до 5.
Список литературы
1. Калиткин Н.Н. Численные методы. – СПб.: БХВ, 2011
2. Бахвалов И.С. Лапин А.В. Чижонков Г.М. Численные методы в задачах и упражнениях. – М.: Бином, 2010.
3. Уилкинсон Дж. Алгебраическая проблема собственных значений. – М.: Мир,1970.
4. Ортега Дж., Рейнболдт В. Итерационные методы решения нелинейных систем уравнений со многими неизвестными. – М.: Мир, 1975.
5. Мысовских И.П. Лекции по методам вычислений. – СПб.: Изд. СПбГУ, 1998.
6. Загускин В.Л. Справочник по численным методам решения алгебраических и трансцендентных уравнений. – М.: ГИФМЛ 1960.
7. Трауб Дж. Итерационные методы решения уравнений. – М.: Мир, 1985.
8. Ахиезер Н. И. Лекции по теории аппроксимации. – М.: Наука, 1965.
9. Бейкер Дж., Грейвс-Моррис П. Аппроксимации Паде. – М.: Мир, 1986.
10. Де Бор К. Практическое руководство по сплайнам. – М.: Радио и связь, 1985.
Завьялов Ю. С., Леус В. А., Скороспелов В. А. Сплайны в инженерной геометрии. – М.: Машиностроение,1985.
Решение систем нелинейных алгебраических уравнений . 19
Дата: 2019-03-05, просмотров: 402.
