Л. Вальраса и В. Леонтьева

Модель Л. Вальраса является макроэкономической моделью, построенной на микроэкономических показателях поведения, на рынках отдельных производителей и потребителей товара. Модель основана на аппарате системы линейных уравнений – для каждого товара выделяется отдельное уравнение. Основную роль в модели играют равновесные цены, обеспечивающие равенство спроса и предложения по каждому товару.

Макроэкономическое равновесие в модели Л. Вальраса означает, что общее предложение конечных продуктов в денежном выражении должно быть равно общему спросу на них как сумме доходов, приносимых всеми факторами производства их собственникам.

Модель Л. Вальраса чисто теоретическая, она показывает рынок в идеале и ставит целью определение общих законов существования экономической системы при наличии множества рынков. В ней сформулированы основные условия структурного соответствия спроса и предложения товаров в условиях совершенной конкуренции. Исключительно важное значение этой модели заключается в том, что она дала толчок к развитию целой системы балансовых моделей макроэкономического равновесия (рис. 16).

Рис. 16. Система моделей макроэкономического равновесия

Модель Л. Вальраса слишком абстрактна и не подвергается эмпирической проверке. Первая, пригодная для практических расчетов эмпирическая модель вошла в экономическую практику под названием «затраты – выпуск». Эта модель основана на балансе межотраслевых связей или межотраслевом балансе (МОБ), в её создании большая роль принадлежит В. Леонтьеву.

Модель «затраты – выпуск» построена на основе структурных взаимозависимостей всех фаз воспроизводства – производства, распределе-ния, обмена и потребления. В. Леонтьев так упростил модель Л. Вальраса, что стало возможным получить ряд параметров для модели, наблюдая за каждым межотраслевым потоком в экономике. С математической и формальной точки зрения модель В. Леонтьева является частным случаем более широкой модели Д. Неймана (1903-1957).

В настоящее время для практических расчетов применяется множество моделей В. Леонтьева «затраты – выпуск», базирующихся на одних и тех же принципиальных основах. Таблица МОБ – это объемный документ, состоящий из многих десятков страниц, поэтому на рис. 17 приведена лишь его схема.

         Отрасль                    Конечное использование

Отрасль                                                                                Всего использовано

 затраты и

ресурсы

           Всего ресурсов

Рис. 17. Принципиальные схемы МОБ

Первый квадрант содержит данные о промежуточном потреблении, которое показывает использование данного продукта различными отраслями-производителями. Это квадратная матрица с отраслями по строкам и столбцам.

Второй квадрант содержит данные о конечном использовании для всех продуктов. Строки соответствуют отраслям-производителям. Столбцы – направления конечного использования: конечное потребление (конечное потребление домашних хозяйств, коллективное потребление), валовое накопление (валовое накопление основного капитала и изменение запасов материальных оборотных средств) и экспорт.

Третий квадрант содержит данные о первичных затратах в каждой отрасли и об общих ресурсах по каждому продукту. Столбцы соответствуют отраслям-производителям, а строки – основным компонентам добавленной стоимости (оплата труда, чистая прибыль, потребление основного капитала, чистые налоги, относящиеся к производству).

Четвертый квадрант, характеризующий перераспределение чистой продукции и не имеющий практического применения, как правило, не используется.

Горизонтальный разрез МОБ (первый и второй квадранты) характеризует процесс распределения продукта, вертикальный (первый и третий квадранты) – процесс создания продукта.

Модель «затраты – выпуск» – это система линейных уравнений (горизонтальный разрез баланса)

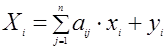, (i = 1, 2, …, n),                                          (14)

или в векторно-матричной форме

Х = АХ + Y.                                                                           (15)

Модель МОБ можно вырезать несколько иначе (вертикальный разрез баланса)

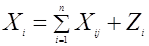, (j = 1, 2, …, n).                                              (16)

Условные обозначения: Х – выпускаемая продукция соответствующих отраслей (Х₁, Х₂, …, Х_n);

Y – выпуск (объёмы) конечного продукта (Y₁, Y₂, …, Y_n);

a_ij – технологические коэффициенты прямых материальных затрат, показывающие, сколько продукции i-отрасли необходимо затратить для производства единицы продукции j-отрасли;

Z – компоненты добавленной стоимости (Z₁, Z ₂, …, Z _n).

Модель МОБ позволяет во-первых, при заданной продукции (Х) определить выпуск конечного продукта (Y); во-вторых, при данном конечном продукте (Y) найти необходимые для его производства объёмы валовой продукции (Х) по отраслям.      

Решение системы уравнений

Х = 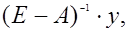                                                                              (17)

где Е – единичная матрица, или

Y = 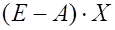.                                                                           (18)

Из модели «затраты – выпуск» в идеале можно получить отраслевое равновесие, межотраслевое равновесие, общее равновесие, т.е. AD = AS.

Ценность моделей МОБ для анализа макроэкономического равновесия велика. В этой модели представлены все основные показатели макроэкономики: валовой выпуск, валовой национальный продукт, национальный доход, промежуточный продукт, конечный продукт, импорт, экспорт и т.д. Кроме того, модель МОБ применяется для специального анализа макроэкономического равновесия трудовых ресурсов и распределения основных производственных фондов.

Возможности МОБ довольно широки для анализа влияния внеэкономических факторов (например, влияния экологии) на макроэкономическое равновесие. МОБ используется также для оценки состояния и тенденций развития мировой экономики. Особую практическую значимость модели «затраты – выпуск» придает тесная связь модели с системой национальных счетов (СНС).

Основные недостатки модели «затраты – выпуск»:

· в модели не учитываются экономические спады и подъемы производства, предприятия- и отрасли-банкроты, дефицит экономики и т.д.;

· между затратами и выпуском принята линейная зависимость, что не всегда соответствует действительности;

· рассматриваются только «чистые отрасли», т.е. отрасли, производящие один продукт;

· в модели достигается статическое равновесие, однако развитие идеи в виде динамической модели снимает частично эту проблему.