Положение скоростной системы координат О1ХСYСZС относительно тангенциальной ОХтYтZт определяется:
- углом поворота траектории j,
- углом наклона траектории q к плоскости местного горизонта в точке доставки,
- углом крена скоростной системы gс.
Таблица 9 - направляющих косинусов, связывающих тангенциальную и скоростную системы координат.
Таблица 9
| Оси | О1ХС | О1YС | О1YС |
| ОХТ | cosjcosq | -cosjsinqcosgc+ sinjsingc | cosjsinqcosgc+ sinjcosgc |
| ОYТ | sinq | cosqcosgc | -cosqsingc |
| ОYТ | -sinjcosq | sinjsinqcosgc+ cosjsingc | cosjcosgc- sinjsinqsingc |
Обозначим матрицу, связывающую орты систем ОХтYтZт и О1ХСYСZС через С {Сij}, где:
 |
Для установления связи между ортами скоростной и связанной системами координат используем тангенциальную систему координат в качестве опорной. Тогда из матричных соотношений
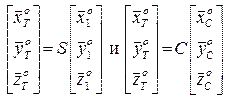
следует
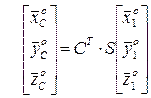
Обозначим матрицу, связывающую орты скоростной и связанной систем через М {mij}=СТS, где:
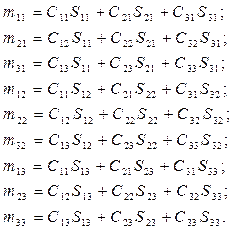
Моделирование БИНС
Схему построения БИНС поясним, рассмотрев типовой вариант конструкции трехканальной БИНС, представленный на рисунке 16. Первичные приемники информации в данном варианте – это 3 акселерометра и 3 датчика угловой скорости (ДУС),измеряющие соответственно проекции кажущегося ускорения и угловых скоростей на оси связанной системы координат. Акселерометры и ДУСы при монтаже на общей плате объединяются в интегральный блок датчиков (ИБД), в котором имеются еще 4 датчика внутренней температуры, таким образом, чтобы выполнялось условие:
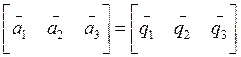
В свою очередь, интегральный блок датчиков жестко размещается на корпусе ЛА таким образом, чтобы связанный с его посадочными местами ортогональный базис совпадал с базисом связанной системы координат ССК.
Наличие блока ДУСов связано с решение задачи ориентации, а наличие блока акселерометров – с решением задач ориентации и навигации.

Рис. 16 Схема построения БИНС
Принцип работы БИНС заключается в построении расчетной системы координат, в которой интегрируются дифференциальные уравнения ориентации и навигации. Расчетная СК в БИНС реализуется аналитически, в отличии от платформенной ИНС, где она реализуется электромеханическими устройствами.
Алгоритм работы БИНС таков: с блока акселерометров и ДУСов в вычислитель подаются сигналы, несущие в себе информацию соответственно о проекциях кажущегося ускорения и проекциях угловой скорости на оси связанной СК. В вычислителе заложен алгоритм, по которому, исходя из полученных данных, рассчитываются навигационные параметры и параметры ориентации. А именно, координаты ЛА в земной СК (широта и долгота), восточная и северная составляющие скорости ЛА, ошибки измерения углов тангажа, крена и курса.
Заложенный в вычислитель алгоритм вычисления навигационных параметров для нашего случая выглядит так:
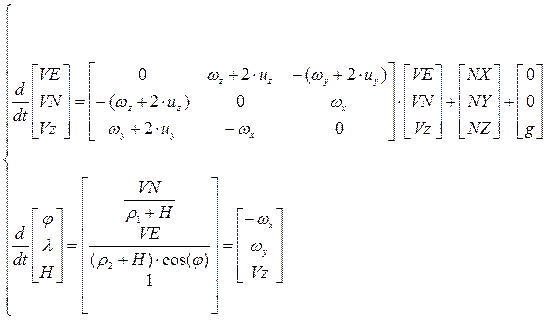 (1)
(1)
где:
VE – восточная составляющая скорости ЛА;
VN – северная составляющая скорости ЛА;
φ – широта – координата местоположения ЛА;
λ – долгота – координата местоположения ЛА;
ωx, ωy, ωz – относительные угловые скорости земной СК.
uy, uz – проекции вектора угловой скорости вращения Земли на оси земной СК;
H – текущая высота полета;
NX, NY, NZ – проекции кажущегося ускорения на оси земной СК;
ρ1, ρ2 – соответственно минимальный и максимальный радиусы кривизны земного эллипсоида;
g – ускорение от силы тяжести.
Стоит отметить, что система 1 записана в форме Коши – удобном для дальнейшего интегрирования виде.
Радиусы кривизны земного эллипсоида определяются следующим образом:
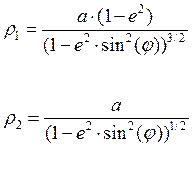
где:
а = 6378245 м – экваториальный полудиаметр (эллипсоид Красовского ПЗ-42);
e2 = 0.0066934126 – эксцентриситет.
Проекции вектора вращения Земли определяются так:
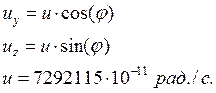
Относительные угловые скорости сопровождающего трехгранника находятся следующим образом:
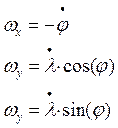
Как уже упоминалось, в данной модели фигурируют проекции кажущегося ускорения на оси сопровождающего трехгранника. А на вычислитель как исходные подаются проекции этих ускорений на оси связанной СК. Возникает вопрос перевода ускорений из связанной СК в земную. Для этого необходимо определить матрицу направляющих косинусов перехода. Так как мы решаем навигационную задачу в горизонтальной СК (земной), то матрица перехода в нее из связанной определяется решением обобщенного уравнения Пуассона вида:
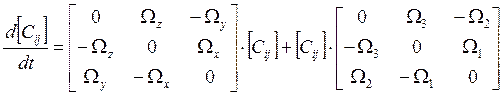 (2)
(2)
где:
Ω1,2,3 – измеряемые угловые скорости (проекции абсолютной угловой скорости вращения горизонтного трехгранника на оси связанной СК);
ΩX,Y,Z – проекции абсолютной угловой скорости вращения горизонтного трехгранника на оси самого трехгранника. Эти элементы определяются следующим образом:
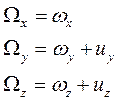
Также матрицу направляющих косинусов можно определить через углы курса, тангажа и крена ЛА:
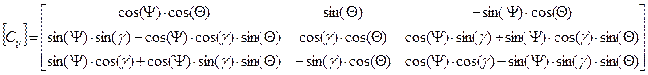
где:
Ψ – текущий угол курса;
γ – текущий угол крена;
θ – текущий угол тангажа.
Мы воспользуемся обоими вариантами, взяв первый за основной, а второй в качестве метода определения начальных значений элементов матрицы направляющих косинусов.
Итак, когда матрица перехода определена, мы можем перейти от связанной СК к земной:
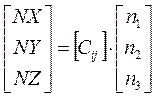
Итак, мы рассмотрели алгоритм расчета навигационных параметров, который реализован в вычислителе БИНСа. Но он является идеальным, так как мы нигде не учитывали ошибок. То есть это – идеальная модель БИНСа.
Для того, чтобы создать реальную модель, необходимо параллельно с идеальной моделью реализовать модель ошибок БИНС, которая имеет вид:
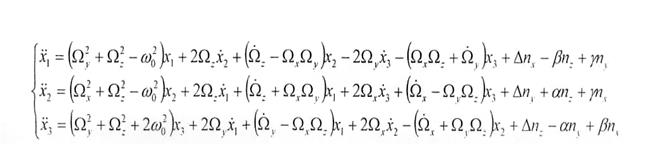

где:
x1 – ошибка определения широты;
х2 – ошибка определения долготы;
х3 – ошибка определения высоты;
α, β, γ – соответственно ошибки определения углов курса, крена и тангажа. Наличие этих ошибок указывает на то, что расчетная СК БИНС не совпадает с сопровождающим горизонтным трехгранником.
Примем:
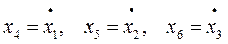
и приведем описанную модель ошибок к удобному для интегрирования виду – к форме Коши:

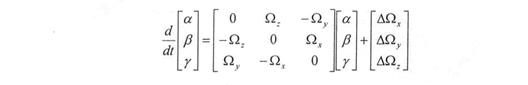
Обозначим эту систему 3. Здесь:
x4 – ошибка расчета восточной составляющей скорости;
х5 – ошибка расчета северной составляющей скорости;
х6 – ошибка расчета вертикальной скорости.
ΔΩX,Y,Z – инструментальные ошибки ДУСов в проекциях на оси земной СК;
ΔnX,Y,Z – инструментальные ошибки акселерометров в проекциях на оси земной СК.
Приведенные инструментальные ошибки акселерометров и ДУСов определяются по формулам:
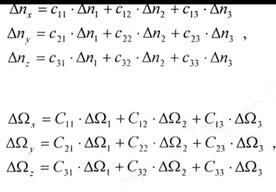
Здесь:
ΔΩ1,2,3 – инструментальные ошибки ДУСов в проекциях на оси связанной СК (они задаются в описании приборов);
Δn1,2,3 – инструментальные ошибки акселерометров в проекциях на оси связанной СК (они задаются в описании приборов).
Итак, подводя итоги данного раздела, надо сказать, что для проведения моделирования БИНС необходимо реализовать описанный выше алгоритм, решающий системы дифференциальных уравнений 1, 2 и 3.
Дата: 2019-03-05, просмотров: 329.