Операции пересечения, объединения, разности и дополнения позволяют формировать новые множества. Однако, как правило, мы не можем сказать, как одно множество соотносится с другим. Например, пусть даны два множества А и В. Пересечение А и В в некотором смысле "меньше" (или по крайней мере не больше), чем А. Действительно, все элементы множества А Ç В принадлежат также множеству А. Из этого наблюдения можно формально определить равенство множеств и различных выражений для того же множества. С помощью этих определений мы также в состоянии написать подходящие логические доказательства важных фактов, относящихся к множествам. Эти результаты, хотя и очевидны, обеспечивают подходящие ситуации, в которых можно ввести некоторые из основных способов доказательств, используемых в дальнейшем.
Доказательство тождественного равенства множеств может быть основано на следующем определении:
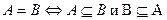
Здесь символ "Û" означает "тогда и только тогда, когда" или "если и только если" и означает эквивалентность двух утверждений. В общем случае мы должны провести доказательство в обе стороны раздельно. Заметим, что эквивалентность может быть легко получена с помощью диаграммы Эйлера - Венна, однако не всегда можно начертить диаграмму, относительно которой можно быть уверенным, что она настолько отвечает требованиям, насколько необходимо.
Доказательство состоит из последовательности утверждений вида "если Р , то Q". Следовательно, если имеется последовательность P0, P1, ..., Pn, такая что P0ÞP1, P1ÞP2, ..., Pn-1ÞPn, то мы имеем прямое доказательство P0ÞPn. В следующих примерах мы покажем, как на практике применить вышеприведенные рассуждения.
Пример 2. Доказать справедливость тождества: А Ç (В È С) = (А Ç В) È (А Ç С).
§ Пусть 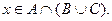 Тогда
Тогда 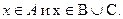 Следовательно,
Следовательно,
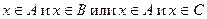 . Следовательно,
. Следовательно, 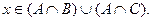
Таким образом, доказано прямое включение рассматриваемых множеств. Обратное включение доказывается путем аналогичных рассуждений.¨
Пример 3. Доказать, что 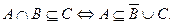
§ В этой задаче нет доказательства тождественного равенства множеств. Подход к решению такого рода задач состоит в том, что доказывается вначале, что из левого утверждения следует правое утверждение и затем обратное следование из правого утверждения левого утверждения. Доказательство проводится в два этапа.
1. Пусть 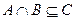 и
и 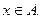 Рассмотрим два случая:
Рассмотрим два случая: 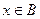 или
или 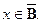 Если
Если 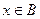 , то
, то 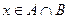 и
и 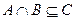 . Если же
. Если же  и
и 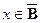 , то
, то 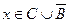 . Следовательно,
. Следовательно, 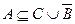 .
.
2. Пусть 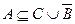 и
и 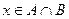 . Тогда
. Тогда  и
и 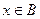 . Следовательно,
. Следовательно, 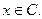 Следовательно,
Следовательно, 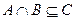 .
.
¨
Пример 4. Доказать, что 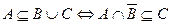 . Доказательство строится аналогично предыдущему.
. Доказательство строится аналогично предыдущему.
Утверждения, доказываемые в примерах 3 и 4, следует также использовать при решении задач, связанных с доказательством тождеств на множествах.
Такие же приемы используются при решении систем уравнений в теории множеств.
Пример 5. Решить систему уравнений
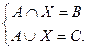
§ 1. Для первого уравнения из определения тождественного равенства множеств запишем:
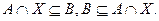 Из второго включения следует:
Из второго включения следует: 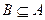 и
и  . Из первого включения, учитывая Пример 3, запишем,
. Из первого включения, учитывая Пример 3, запишем, 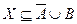 . Объединив полученные результаты, получим
. Объединив полученные результаты, получим 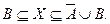
2. Для второго уравнения запишем аналогично: 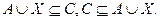 Из первого включения получим
Из первого включения получим 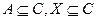 . Из второго включения, учитывая пример 4, получим
. Из второго включения, учитывая пример 4, получим 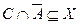 . Объединяя полученные включения, получим
. Объединяя полученные включения, получим 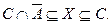
3. Теперь нужно объединить два двойных неравенства, полученные в пунктах 1 и 2. В соответствии с определением отношения включения, части неравенств, стоящие слева от знака Í, следует соединить операцией объединения, а стоящие справа – операцией пересечения:
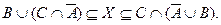 Если множества, входящие в это двойное неравенство одинаковы, то можно сделать вывод относительно множества X. Преобразуем левое множество с целью получить выражение, совпадающее с правым множеством.
Если множества, входящие в это двойное неравенство одинаковы, то можно сделать вывод относительно множества X. Преобразуем левое множество с целью получить выражение, совпадающее с правым множеством.
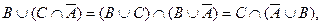 так как ранее было получено, что
так как ранее было получено, что 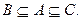 Следовательно, X=
Следовательно, X= 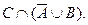
¨
Пример 6. В некоторых случаях оказывается полезным соотношение:
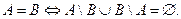
Докажем его.
§ По определению тождественного равенства множеств: 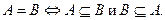 По определению включения
По определению включения 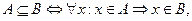 следовательно,
следовательно, 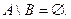 Аналогично из второго включения получим:
Аналогично из второго включения получим: 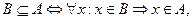 следовательно
следовательно 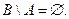 Следовательно, исходное соотношение справедливо, так как объединение пустых множеств пусто.
Следовательно, исходное соотношение справедливо, так как объединение пустых множеств пусто.
¨
Пример 7. Доказать, что любое уравнение относительно множества Х, в правой части которого стоит пустое множество Æ, равносильно уравнению: 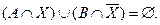
§ Докажем вначале, что левая часть уравнения может быть представлена в предложенной форме. Действительно, предложенная форма представляет собой НФК, в которой может быть представлено любое множество путем применения аксиом и тождеств алгебры Кантора к исходному уравнению, как это было описано выше. А и В – это формулы, являющиеся пересечением конечного числа множеств.
Далее, исходя из определения операции объединения множеств, заключаем, что объединение двух множеств пусто тогда и только тогда, когда оба эти множества пусты.
Получив НФК, приравняем нулю каждое из полученных слагаемых. В соответствии с предыдущими рассуждениями, из равенства пересечения двух множеств пустому множеству следуют включения: 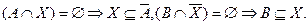 Следовательно,
Следовательно, 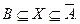 Здесь А и В – произвольные множества. Решение существует, если выполняется полученное двойное включение.
Здесь А и В – произвольные множества. Решение существует, если выполняется полученное двойное включение.
¨
Опишем метод решения системы двух уравнений относительно неизвестного множества Х, основанный на примерах 6 и 7.
- Учитывая пример 6, заменить каждое уравнение системы на уравнения, в правой части которых стоит 0.
- Записать каждое уравнение в виде объединения пересечений пустых множеств.
- Учитывая пример 7, записать условия существования решения.
- Найти решение.
Рассмотрим применение этого метода.
Пример 8. Решить систему уравнений:
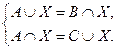
§ 1. Из первого уравнения имеем:
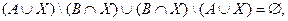
отсюда в результате преобразований получим:
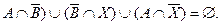
Отсюда получим неравенства:
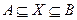 и
и 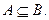
2. Из второго уравнения:
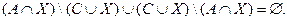
После преобразований получим:
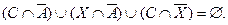
Отсюда получим:
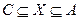 и
и 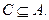
- Объединяя двойные неравенства, полученные в пунктах 1 и 2, получим:
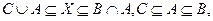 откуда сразу получаем:
откуда сразу получаем:
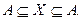
Следовательно, X=A.
¨
Дата: 2019-03-05, просмотров: 351.