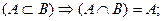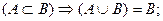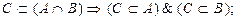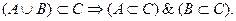В общем случае алгебра - это совокупность несущего множества и заданных на нем отношений и операций. В алгебре Кантора (алгебре множеств) несущим множеством является булеан универсума, на котором заданы три операции: одноместная операция НЕ ( 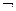), двуместные операции И (Ç) и ИЛИ (È). Обозначение алгебры Кантора: . Операции на множествах подчинены простым законам, перекликающимся с аксиомами алгебры чисел, но не совпадающим с ними. Аналогом операции Ç в алгебре чисел является операция умножения, операции È - сложение. Однако эти аналогии в значительной степени внешние. Законы алгебры множеств более универсальны, чем законы алгебры чисел.

Аксиомы алгебры Кантора

А1. Тождественности:	А È А=А ;	А Ç А=А;
А2. Коммутативности:	А ÈВ=В È А;	А ÇВ= В ÇА;
А3.Ассоциативности:	А È (В ÈС)=(А È В) È С;	А Ç(В ÇС)=(А ÇВ) ÇС;
А4. Дистрибутивности:	А È(В ÇС)=(А ÈВ) Ç (А ÈС);	А Ç(В ÈС)= (А ÇВ) È(А ÇС);
А5. Поглощения:	AÇ(AÈB)=A	AÈ(AÇB)=A
А6.Законы дополнения:	А ÈI=I; А ÈÆ=А; А È`А =I; `I =Æ ;	А Ç 1=А; А Ç Æ= Æ; А Ç `А = Æ; `Æ=1;
А6. Закон двойного отрицания: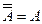
Правила де'Моргана: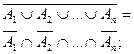

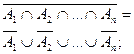
Законы для разности множеств

1. А\В=АÇ`В

2. 1\А= `А

3. А\1=Æ

4. А\Æ=А

5. Æ\А=Æ

6. А\А=Æ

7.

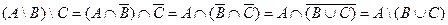
8.

9.

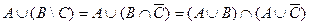
10. А Ç(В\С)=(А ÇВ)\(А ÇС)

Кроме этих отношений на множествах полезно помнить следующие, вытекающие из определений, отношения:

Используя аксиомы и тождества алгебры множеств можно преобразовывать исходные множества, заданные формулами, к формулам определенного вида. Наибольший интерес представляют  канонические формы представления. Одной из канонических форм представления множеств является  нормальная форма Кантора, т.е. представление множества в виде объединения пересечений множеств или их дополнений. Стратегия преобразований исходной формулы состоит в следующем:

1. Вначале избавляются от всех вхождений знака "вычесть" (\) в исходной формуле.

2. Используя правила де Моргана, заменяют дополнения выражений на объединение и пересечение дополнений.

3. Используя аксиомы дистрибутивности, преобразуют полученное выражение к требуемому виду.

Пример 1.

 А\(В\С)=А Ç(В Ç `С ) = А Ç(`В È С ) = (А Ç `В) È(А ÇС).

Полученная формула есть нормальная форма Кантора данной формулы (НФК).