Таблица 6.1 - Обозначение физических величин
| Наименование физической величины | Обозначение | Единицы измерения |
| Случайное сообщение | ai | -- |
| Вероятность случайного сообщения | P(ai) | -- |
| Количество информации в сообщении | I(ai) | бит |
| Энтропия источника | H | бит |
| Коэффициент избыточности источника | χ и | -- |
| Производительность источника | H' | бит/с |
Примеры решения задач:
Задача 1. Определите количество информации в слове русского текста из 10 букв, если вероятность появления всех букв слова одинаковая.
Решение: Определим вероятность появления одной буквы русского алфавита
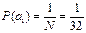
Тогда, количество информации, содержащееся в одной букве определим по формуле
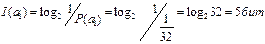
Тогда, количество информации, содержащееся в слове русского текста из 10 букв
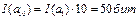
Задачи для самостоятельного решения:
6.1 Какому понятию соответствует определение: "… … - это среднее количество информации, приходящееся на одно сообщение источника".
Варианты ответов:
 а) производительность источника; в) энтропия источника;
а) производительность источника; в) энтропия источника;
б) пропускная способность; г) избыточность источника.
6.2 Энтропия источника дискретных сообщений определяется выражением:
Варианты ответов: а) 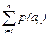
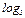
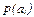 ; б)
; б) 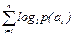 ;
;
в) 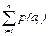
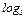
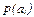 ; г)
; г) 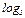
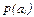 .
.
6.3 Энтропия источника максимальная, если:
Варианты ответов:
а) вероятности отдельных сообщений различны;
б) все сообщения равновероятны;
в)нет правильного ответа.
6.4 Дополните текст: «… сообщения тем больше, чем … количество информации оно несет».
6.5 Двоичный источник без памяти формирует сообщение 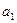 с вероятностью 0,3 и сообщение
с вероятностью 0,3 и сообщение 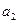 с вероятность 0,7. Какое количество информации содержит каждое сообщение
с вероятность 0,7. Какое количество информации содержит каждое сообщение 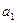 и
и 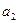 ? Вычислите среднее количество информации, создаваемое источником при выдаче одного сообщения.
? Вычислите среднее количество информации, создаваемое источником при выдаче одного сообщения.
6.6 Определите энтропию, если количество сообщений равно 15, вероятность появления сообщений 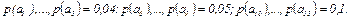 Как изменится энтропия, если
Как изменится энтропия, если 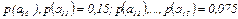 ?
?
6.7 На выходе микрофона формируется сигнал в полосе 30…15000 Гц, который затем дискретизируется и квантуется равновероятными уровнями. Определите производительность источника сообщений, если вероятность появления в квантованном сигнале каждого уровня составляет 0,125.
6.8 Определите производительность телеграфного аппарата, используемого в качестве источника сообщений. Аппарат используется для передачи осмысленного русского текста, коэффициент избыточности текста 0,5, время передачи одной буквы текста 0,04 с.
6.9 Рассчитайте энтропию источника сообщений, если вероятности появления сообщений 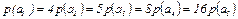 . Определите количество информации, содержащейся в сообщении с вероятностью появления 0,125 р(а1). Источник выдает независимые сообщения.
. Определите количество информации, содержащейся в сообщении с вероятностью появления 0,125 р(а1). Источник выдает независимые сообщения.
6.10 Рассчитайте энтропию если количество сообщений – 18, а вероятность их появления 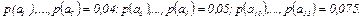 Как изменится энтропия, если
Как изменится энтропия, если 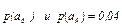 , а
, а 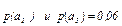 ?
?
6.11 Рассчитайте коэффициент избыточности источника сообщений, если вероятность появления сообщений 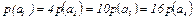 . Источник выдает независимые сообщения.
. Источник выдает независимые сообщения.
6.12 Среднее количество информации при передаче 1728 сообщений составляет 4,45 бит. Рассчитайте коэффициент избыточности источника сообщений, формирующего независимые сообщения, и количество информации, содержащейся в сообщении с вероятностью появления 0,2.
6.13 Определите пропускную способность двоичного канала, если скорость модуляции в нем 600 Бод и вероятность ошибки 10 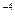 . Насколько отличается пропускная способность этого канала от идеального?
. Насколько отличается пропускная способность этого канала от идеального?
6.14 Определите максимальную скорость передачи информации по непрерывному каналу связи шириной 4 кГц, если средняя мощность сигнала равна 14,8 мВт, мощность помехи 0,9 мВт.
6.15 Определите ширину спектра сигнала, передаваемого по непрерывному каналу связи, если максимальная скорость передачи информации равна 8,44 Мбит/ c, мощность сигнала в канале 19 мВт, мощность помех 1 мВт.
6.16 Телевизионное изображение состоит из 485000 элементов. Каждый из этих элементов может иметь 9 различных градаций яркости, все градации яркости равновероятны. За одну секунду передается 25 кадров изображения. Определите пропускную способность канала связи, необходимую для передачи сообщений от источника заданной производительности; ширину полосы частот канала, необходимую для передачи телевизионного изображения при отношении мощности сигнала к мощности помехи равном 1350.
6.17 Определите мощность помех (белый шум) в канале с полосой частот 312,3…359,4 кГц, если средняя мощность сигнала равна 412 мкВт, пропускная способность канала 315,6 кбит/ c.
6.18 Рассчитайте допустимую мощность помех (белый шум) в канале, если на его вход подан телефонный сигнал средней мощностью 32 мкВт, максимальная скорость передачи сигнала в канале составляет 64 кбит/ c.
Цифровая обработка сигналов
7.1 На месте многоточия впишите недостающие в определении слова: «Сумма ряда по …… степеням…… переменной, соответствующая числовой ……, содержащей отсчетные значения, называется Z -преобразованием»
7.2 Укажите среди перечисленных формул выражение для определения обратного Z - преобразования.
Варианты ответов:
а) 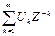 ; б)
; б) 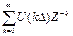 ;
;
в) 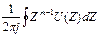 ; г)
; г) 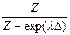
7.3 Допишите формулу Z-преобразования дискретного сигнала 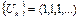 U ( Z )=
U ( Z )= 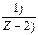
7.4 Найдите Z-преобразование для заданного сигнала U К= 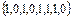 .
.
7.5 Укажите, какие из приведенных коэффициентов можно рассчитать с помощью следующих математических формул
Формулы: 1) 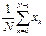 ; 2)
; 2) 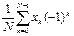 ;
;
3) 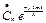 ; 4)
; 4) 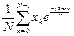
Коэффициенты:
а) коэффициенты прямого дискретного преобразования Фурье;
б) постоянную составляющую дискретного преобразования Фурье
в) коэффициенты обратного дискретного преобразования Фурье;
г) коэффициенты дискретного преобразования Фурье при N- четном
7.6 Допишите формулу для расчета постоянной составляющей дискретного преобразования Фурье С0= 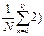
7.7 Определите постоянную составляющую и четвертый коэффициент дискретного преобразования Фурье для заданного сигнала. Изобразите их графически хк = 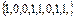
7.8 Подсчитайте и сравните число операций вычисления при передаче последовательности длиной N методами дискретного преобразования Фурье и быстрого преобразования Фурье при следующих исходных данных N=1024
7.9 Изобразите графически и объясните принцип действия операции "бабочка" при прореживании данных по частоте и по времени
Дата: 2019-03-05, просмотров: 435.