Таблица 2.1 – Обозначение физических величин
| Наименование физической величины | Обозначение | Единицы измерения |
| Амплитуда гармонических составляющих спектра | Am1, Am2…AmN Um1, Um2…UmN Im1, Im2…ImN | В, Вольт; А, Ампер |
| Амплитуда постоянной составляющей спектра | 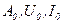
| В, Вольт; А, Ампер |
| Ширина спектра сигнала (ширина полосы частот) | 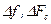
| Гц, Герц |
| Длительность импульса | tи ,τ | с, секунда |
| Период следования импульсов | T | c, секунда |
| Частота следования импульсов | F, f | Гц, Герц |
| Угловая частота | 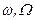
| рад/с, радиан в секунду |
| Циклическая частота | 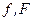
| Гц, Герц |
| Скважность импульсов | 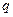
| -- |
| Спектральная плотность амплитуд сигнала | 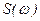
| В/рад/с, Вольт на радиан/с; А/рад/с, Ампер на радиан/с. |
Примеры решения задач:
Задача 1. Рассчитайте спектр периодической последовательности прямоугольных импульсов (ПППИ), если амплитуда импульсов 200 мА, частота следования импульсов 1000 Гц, длительность импульсов 0,25 мс. Расчет произвести для значений частот в пределах принятой ширины спектра ПППИ.
Дано: Im =200 мА f =1000 Гц t и =0,25 мс
Решение: Амплитуду постоянной составляющей рассчитаем по формуле
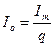 , где q – скважность импульсов.
, где q – скважность импульсов.
Определим скважность:
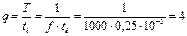
Тогда 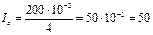 мА.
мА.
Рассчитаем амплитуды гармонических составляющих. Для этого воспользуемся формулой 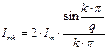 , где k – номер гармоники.
, где k – номер гармоники.
Ширина спектра ПППИ ограничивается двумя лепестками. Количество гармоник в спектре определяется как q -1. Амплитуды гармоник, номера которых кратны скважности, равны нулю. Тогда
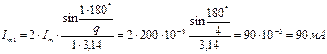 ;
;
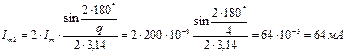 ;
;
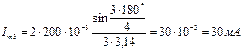 ;
;
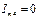 мА;
мА;
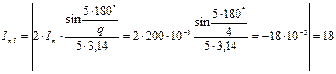 мА;
мА;
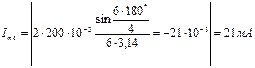 ;
; 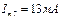 ;
; 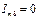 мА.
мА.
Частота первой (основной) гармоники в спектре ПППИ равна частоте следования импульсов.
Тогда f 1 =1000 Гц=1 кГц; f 2 =2 ·f 1 =2 кГц; f 3 =3 ·f 1 =3 кГц; f 4 =4 кГц;
f 5 =5 кГц; f 6 =6 кГц; f 7 =7 кГц; f 8 =8 кГц.
Построим спектральную диаграмму амплитуд
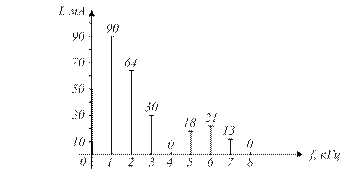
Задача 2. Рассчитайте спектральную плотность одиночного прямоугольного импульса длительностью 5 мкс и амплитудой 2 В на частотах 50 и 100 кГц. Определите ширину спектра одиночного прямоугольного импульса. Постройте спектральную диаграмму.
Дано: tu =5мкс Um =2 B f 1 =50кГц f 2 =100кГц
Решение: Спектральную плотность амплитуд одиночного прямоугольного импульса (ОПИ) будем рассчитывать по формуле
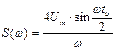 , где
, где 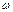 - угловая частота, для которой рассчитывается спектральную плотность амплитуд. Угловую частоту определим по формуле
- угловая частота, для которой рассчитывается спектральную плотность амплитуд. Угловую частоту определим по формуле
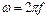 . Тогда
. Тогда
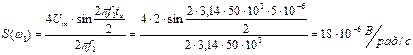
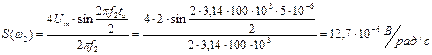
Ширину спектра ОПИ рассчитаем по формуле
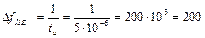 кГц.
кГц.
Чтобы построить спектральную диаграмму необходимо определить спектральную плотность амплитуд на частоте ω =0:
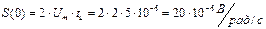 .
.
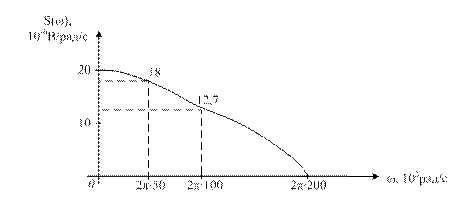
Построим спектральную диаграмму амплитуд
Задачи для самостоятельного решения:
2.1 Вставьте недостающие слова: «Чем … длительность импульса, тем … его спектр».
2.2 Вставьте недостающие слова: «На практике шириной … считают эффективную область …, в пределах которой сконцентрировано 90…95% энергии сигнала».
2.3 Какие из формул дают разложение периодического колебания в совокупность гармонических колебаний с кратными частотами?
Варианты ответов:
а) 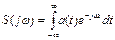 ; б)
; б) 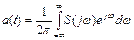 ;
;
в) 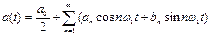 ;
;
г) 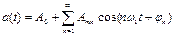 ;
;
д) 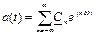 ; е) нет правильного ответа.
; е) нет правильного ответа.
2.4 Какая из формул позволяет отыскать форму непериодического сигнала по его спектральной плотности? Как называется эти соотношение?
Варианты ответов:
а) 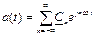 ; б)
; б) 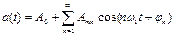 ;
;
в) 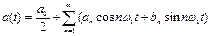 ;
;
г) 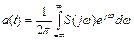 ; д)
; д) 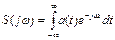
2.5 Какая из формул дает разложение непериодического колебания в совокупность гармонических колебаний с непрерывным спектром частот?
Варианты ответов:
а) 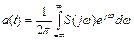 ; б)
; б) 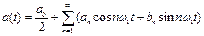 ;
;
в) 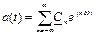 ; г)
; г) 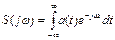 ;
;
д) 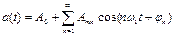 .
.
2.6 Какая из формул дает разложение периодического колебания в совокупность периодических экспоненциальных функций? Как называется это соотношение?
Варианты ответов:
а) 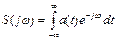 ; б)
; б) 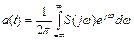 ;
;
в) 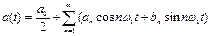 ;
;
г) 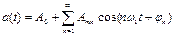 ;
;
д) 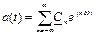 .
.
2.7 Какое представление, двустороннее или одностороннее (не имеющее отрицательных частот), дает выражение г) в условии задачи 2.6?
2.8 На вход анализатора спектра подается последовательность прямоугольных импульсов с частотой следования 100 кГц и скважностью 4. Нарисуйте спектральную диаграмму амплитуд, которую рисует луч на экране электронно-лучевой трубки анализатора спектра, если амплитуда импульсов равна 2,5 В.
2.9 Амплитуда постоянной составляющей в спектре периодической последовательности прямоугольных импульсов (ПППИ) 2 В, период следования импульсов 10 мкс, длительность импульсов 2,5 мкс. Рассчитайте спектральный состав периодической последовательности прямоугольных импульсов и определите ширину спектра. По результатам расчета постройте временную и спектральную диаграммы ПППИ.
2.10 Рассчитайте ширину спектра ПППИ и амплитуду третьей гармоники, если частота следования импульсов равна 25 кГц, скважность импульсов равна 2, амплитуда постоянной составляющей спектра 1 В.
2.11 Рассчитайте спектральный состав периодической последовательности прямоугольных импульсов (ПППИ), определите ширину спектра, если период следования импульсов 40 мкс, скважность импульсов 4, амплитуда второй гармоники в спектре ПППИ равна 5В. По результатам расчета постройте временную и спектральную диаграммы.
2.12 Сравните спектры периодических импульсных последовательностей. приведенных на рисунке 2.1.



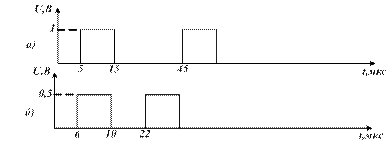
Рисунок 2.1− Временные диаграммы ПППИ
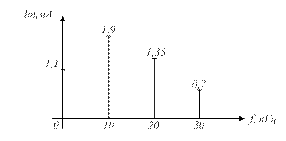
2.13 На рисунке 2.2 приведена спектральная диаграмма последовательности прямоугольных импульсов. Определите длительность, скважность, частоту следования и постоянную составляющую, если амплитуда импульсов равна 1,6 В, период следования 10 мс.
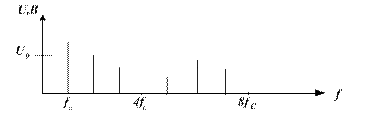

Рисунок 2.2 − Спектральная диаграмма ПППИ
2.14 Рассчитайте амплитуду и частоту следования периодической последовательности прямоугольных импульсов (ПППИ), если скважность импульсной последовательности равна 4, длительность импульса 5 мкс, амплитуда первой гармоники в спектре импульсной последовательности равна 2 В. По результатам расчета постройте в масштабе временную диаграмму ПППИ.
2.15 Рассчитайте спектральной состав периодической последовательности прямоугольных импульсов (ПППИ) в пределах выбранной ширины спектра, если амплитуда импульсов равна 3 В, ширина спектра ПППИ равна 100 кГц, период следования импульсов 60 мкс. По результатам расчета постройте спектральную диаграмму амплитуд.
2.16 Рассчитайте амплитуды составляющих спектра последовательности прямоугольных импульсов (рисунок 2.3) и определите длительность импульсов, если амплитуда импульсов равна 5 В. Нарисуйте в примерном масштабе временную диаграмму рассматриваемой последовательности импульсов.
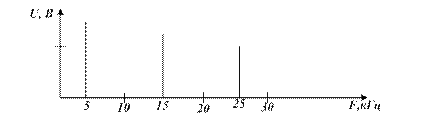
Рисунок 2.3 − Спектральная диаграмма ПППИ
2.17 На вход анализатора спектра подается последовательность прямоугольных импульсов с частотой следования 100 кГц и скважностью 4. Нарисуйте спектральную диаграмму амплитуд, которую рисует луч на экране электронно-лучевой трубки анализатора. Рассчитайте амплитуды пяти первых гармоник спектра, если амплитуда импульсов равна 2,5 В.
2.18 Периодическая последовательность прямоугольных импульсов (ПППИ) задана на одном периоде математической моделью 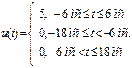 . Определите период и скважность ПППИ. Рассчитайте амплитуды спектральных составляющих в пределах выбранной ширины спектра.
. Определите период и скважность ПППИ. Рассчитайте амплитуды спектральных составляющих в пределах выбранной ширины спектра.
2.19 Как изменится спектр периодической последовательности прямоугольных импульсов, указанной в задаче 1.76, если ее скважность увеличить в два раза, сохранить постоянными амплитуду импульсов и их длительность? Рассчитайте амплитуду третьей гармоники спектра и постоянную составляющую.
2.20 Сравните спектры периодических импульсных последовательностей, приведенных на рисунке 2.4.
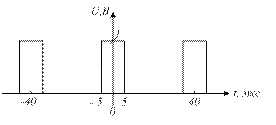
| 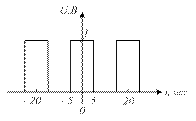
|
Рисунок 2.4 – Временные диаграммы сигналов
2.21 Постройте спектральную диаграмму амплитуд периодической последовательности видеоимпульсов, представленной на рисунке 2.5, в пределах принятой ширины спектра.
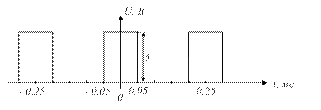
Рисунок 2.5 – Временная диаграмма сигнала
2.22 На вход приемного устройства, настроенного на частоту 500 кГц воздействует помеха в виде периодической последовательности прямоугольных импульсов амплитудой 5 мВ, следующих с периодом 40 мкс и длительностью импульсов 5 мкс. В полосу пропускания приемника попадает одна из гармоник периодической последовательности. Определите номер этой гармоники и амплитуду помехи на выходе приемника.
2.23 Угловые частоты соседних спектральных составляющих периодической последовательности прямоугольных импульсов (ПППИ) отличаются на величину 2π∙104 рад/с. Длительность импульсов равна 10мкс, а постоянная составляющая равна 0,15 В. Рассчитайте амплитуду импульсов, период следования импульсов, ширину спектра ПППИ. Постройте временную диаграмму ПППИ.
2.24 Рассчитайте спектральную плотность одиночного прямоугольного импульса амплитудой 3 В, длительностью 10 мкс на частоте 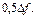
2.25 Рассчитайте спектральную плотность одиночного импульса, временная диаграмма которого приведена на рисунке 2.6, на частотах 0,5 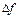 и 0,75
и 0,75 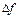 . Если
. Если 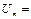 2 В.(
2 В.( 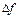 -ширина спектра сигнала). Определите ширину спектра импульса.
-ширина спектра сигнала). Определите ширину спектра импульса.
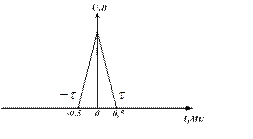
Рисунок 2.6 − Временная диаграмма импульса
2.27 Рассчитайте спектральную плотность импульса (рисунок 2.6) на пяти частотах в пределах выбранной ширины спектра импульса. По результатам расчета постройте спектральную диаграмму.
2.28 Рассчитайте ширину спектра и спектральную плотность амплитуд на частотах 4 и 20 кГц сигнала передачи данных (СПД), если длительность импульса СПД равна 20 мкс, амплитуда импульса 5 мА.
ПРЕОБРАЗОВАНИЕ СИГНАЛОВ В НЕЛИНЕЙНЫХ ЦЕПЯХ
Таблица 3.1 – Обозначение физических величин
| Наименование физической величины | Обозначение | Единицы измерения |
| Амплитуда гармонических составляющих спектра | Am1, Am2…AmN Um1, Um2…UmN Im1, Im2…ImN | В, Вольт; А, Ампер |
| Амплитуда постоянной составляющей спектра | 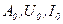
| В, Вольт; А, Ампер |
| Угол отсечки | Θ | °, градусы |
| Крутизна вольтамперной характеристики | S | А/В, Ампер на Вольт |
| Период следования импульсов | T | c, секунда |
| Частота следования импульсов | F, f | Гц, Герц |
| Угловая частота | 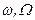
| рад/с, радиан в секунду |
| Циклическая частота | 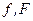
| Гц, Герц |
| Напряжение смещения | Uo | В, Вольт |
| Напряжение отсечки | Uн | В, Вольт |
| Амплитуда воздействия | Um | В, Вольт |
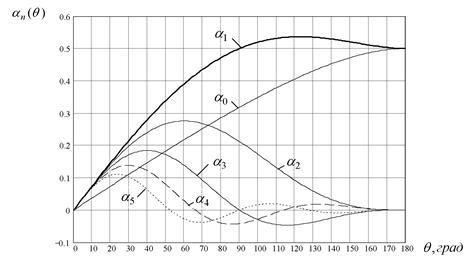
Рисунок 3.1 – Графики функций Берга
Примеры решения задач:
Задача 1. Вставьте недостающие слова: «… аппроксимация – это представление реальной вольтамперной характеристики в виде… n -ой степени».
Решение: Согласно [1], в задаче приведено неполное определение полиномиальной (степенной) аппроксимации, т.е «полиномиальная аппроксимация – это представление реальной вольтамперной характеристики в виде полинома (многочлена) n -ой степени».
Задача 2. На вход нелинейного элемента (НЭ) подано напряжение 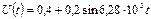 , амплитуда тока на выходе нелинейного элемента равна 5 мА, напряжение отсечки 0,5 В. Рассчитайте спектр отклика нелинейного элемента, постройте спектральную диаграмму тока отклика.
, амплитуда тока на выходе нелинейного элемента равна 5 мА, напряжение отсечки 0,5 В. Рассчитайте спектр отклика нелинейного элемента, постройте спектральную диаграмму тока отклика.
Дано: Uo =0,4 В Um =0,2 В Im =5 мА U н =0,5В ω =6,28 · 103рад/с
Решение: Амплитуды гармонических составляющих тока отклика НЭ определим по формуле 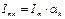 , где
, где 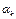 - коэффициенты Берга, значения которых определяются углом отсечки Θ .
- коэффициенты Берга, значения которых определяются углом отсечки Θ .
Рассчитаем угол отсечки. Для этого воспользуемся формулой
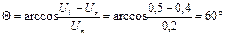
По графику 3.1 определим значения коэффициентов 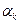 :
:
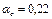 ;
; 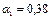 ;
; 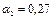 ;
; 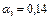 .
.
Рассчитаем амплитуды тока отклика:
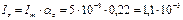 А;
А; 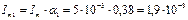 А;
А;
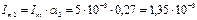 А;
А; 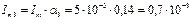 А;
А;
На вход НЭ подано гармоническое колебание. В этом случае отклик НЭ представляет собой негармоническое периодическое колебание. Известно, что спектр периодической функции дискретный с частотами кратными основной (первой). Частота основной гармоники равна частоте периодической функции.
В нашем случае f 1 = f след.имп . = f вх = ω /2 π =10 · 103 Гц=10 кГц. Тогда частоты 2-ой и 3-ей гармоник f 2 =2 ·f 1 =20 кГц, f 3 =3 ·f 1 =30 кГц. Частота постоянной составляющей равна 0.
Построим спектральную диаграмму тока отклика.
Задачи для самостоятельного решения:
3.1 На каком из рисунков 3.2 приведено условное графическое обозначение нелинейного резистора?
Варианты ответов:

Рисунок 3.2 −Резисторы. Условное обозначение
3.2 Какие из перечисленных изделий относятся к резистивным нелинейным элементам?
Варианты ответов:
а) резистор, трансформатор с ферромагнитным сердечником;
б) варикап, катушка индуктивности с ферромагнитным сердечником;
в) полупроводниковый диод, транзистор;
г) электронная лампа, варикап;
д) нет правильного ответа.
3.3 Как называется внешняя характеристика нелинейной индуктивности?
Варианты ответов:
а) вольтамперная; б) вольтфарадная; в) вебер-амперная; г) вольткулонная.
3.4 Дайте определение термина аппроксимация вольтамперной характеристики нелинейного элемента.
3.5 Какой способ аппроксимации характеристики нелинейного элемента целесообразно использовать при больших амплитудах входного сигнала?
Варианты ответов:
а) полиноминальный; б) экспоненциальный;
в) трансцендентными функциями; г) кусочно-линейный.
3.6 Перечислите основные свойства нелинейных элементов.
3.7 Дайте определение понятиям нелинейный, линейный и параметрический элемент.
3.8 На каком графике приведена характеристика сопротивления при использовании в качестве нелинейного элемента полупроводникового диода?
Варианты ответов:
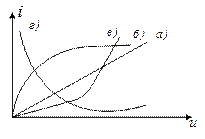
Рисунок 3.3 – Внешние характеристики элементов
3.9 На каком из рисунков приведена спектральная диаграмма отклика нелинейного элемента при гармоническом воздействии?
Варианты ответов:
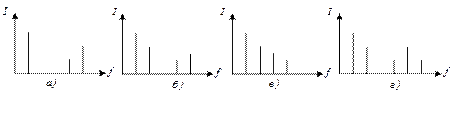
Рисунок 3.4 − Спектры сигналов
3.10 На каком из рисунков приведена временная диаграмма отклика нелинейного элемента при гармоническом воздействии и угле отсечки 1000?
Варианты ответов:
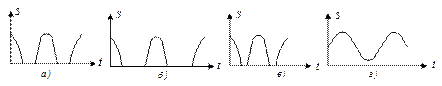
Рисунок 3.5 − Временные диаграммы
3.11 Чему равно статическое сопротивление нелинейного элемента в точке А вольтамперной характеристики, приведенной на рисунке 3.6?
Варианты ответов:
а) котангенсу угла, образованного осью абсцисс и прямой, соединяющей начало координат с точкой А;
б) 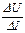 ; в)
; в) 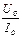 ;
;
г) котангенсу угла, образованного осью абсцисс и касательной к ВАХ в точке А.
3.12 Где должна быть выбрана рабочая точка на характеристике нелинейного элемента, чтобы угол отсечки был равен 700?
Варианты ответов:
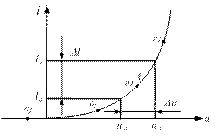
Рисунок 3.6 − Вольтамперная характеристика нелинейного элемента
3.13 Как изменится спектр отклика нелинейного элемента при гармоническом воздействии, если вместо нелинейного элемента с характеристикой 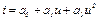 использовать нелинейный элемент с характеристикой
использовать нелинейный элемент с характеристикой 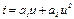 .
.
Варианты ответов:
а) в спектре появятся новые гармоники;
б) изменится амплитуда первой гармоники;
в) изменится амплитуда постоянной составляющей;
г) спектр не изменится.
3.14 Рассчитайте статическое и дифференциальное сопротивления нелинейного элемента, характеристика которого приведена на рисунке 3.7. Напряжение смещения равно 0,3 В, на вход подано колебание 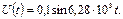
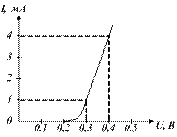
Рисунок 3.7 − Вольтамперная характеристика нелинейного элемента
3.15 Рассчитайте статическое и дифференциальное сопротивления нелинейного элемента, характеристика которого приведена на рисунке 3.7, если напряжение смещения равно 0,4 В, на вход нелинейного элемента подано гармоническое колебание частотой 500 Гц и амплитудой 0,1 В. Сравните результаты расчета с результатами, полученными при решении задачи 3.11.
3.16 Что показывает значение крутизны вольтамперной характеристики нелинейного элемента 6 мА/В?
Варианты ответов:
а) при изменении входного напряжения на 1В выходной ток нелинейного элемента изменится на 6 мА;
б) при изменении входного напряжения на 6В выходной ток нелинейного элемента изменится на 1 мА;
в) угол касательной в градусах, проведенной к рабочей точке ВАХ;
г) при изменении выходного напряжении на 1 В выходной ток изменится на 6 мА.
3.17 Вставьте недостающие слова: «… является цепь, у которой параметры зависят и от времени и от протекающего тока или приложенного напряжения».
3.18 Вольтамперная характеристика (ВАХ) нелинейного элемента аппроксимирована кусочно-линейным способом (см. рисунок 3.8). Составьте аналитическое выражение, описывающее заданную ВАХ.
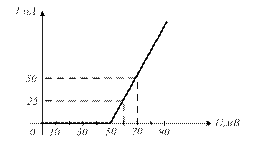
Рисунок 3.8 – ВАХ нелинейного элемента
3.19 Вольтамперная характеристика нелинейного элемента аппроксимируется полиномом 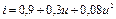 . Определите спектральный состав отклика, если на вход нелинейного элемента воздействует гармоническое колебание
. Определите спектральный состав отклика, если на вход нелинейного элемента воздействует гармоническое колебание 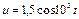 . Постройте спектральную диаграмму отклика. Для каких целей можно использовать нелинейный элемент, работающий в данном режиме?
. Постройте спектральную диаграмму отклика. Для каких целей можно использовать нелинейный элемент, работающий в данном режиме?
3.20 Приведено аналитическое выражение, описывающее вольтамперную характеристику (ВАХ) нелинейного элемента. Используя содержащиеся в нём данные, постройте ВАХ.
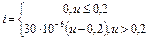
3.21 Определите постоянную составляющую и амплитуды первых трех гармоник отклика на выходе нелинейного элемента, аппроксимируемого кусочно-линейным способом (рисунок 3.9). Постройте спектральную диаграмму отклика. Как необходимо изменить режим работы нелинейного элемента, чтобы увеличить амплитуду тока второй гармоники?

Рисунок 3.9 −Воздействие на нелинейный элемент
3.22 Определите амплитуды первых трех гармоник отклика на выходе нелинейного элемента, аппроксимируемого кусочно-линейным способом (рисунок 3.10). Нарисуйте спектральную диаграмму отклика, если частота гармонического колебания на входе нелинейного элемента равна 200 кГц.

Рисунок 3.10 − Воздействие на нелинейный элемент
3.23 На рисунке 3.11 приведена проходная характеристика транзистора КТ349. На входные электроды транзистора подано напряжение смещения 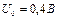 и гармоническое колебание
и гармоническое колебание 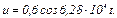 Рассчитайте спектральный состав отклика нелинейного элемента. Каким необходимо выбрать напряжение смещения, чтобы получить на выходе максимальную амплитуду тока второй гармоники?
Рассчитайте спектральный состав отклика нелинейного элемента. Каким необходимо выбрать напряжение смещения, чтобы получить на выходе максимальную амплитуду тока второй гармоники?
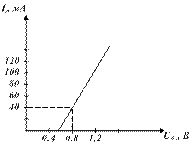
Рисунок 3.1 − Проходная характеристика транзистора
3.24 На вход транзистора, проходная характеристика которого приведена на рисунке 3.11, подано гармоническое колебание частотой 5 кГц. Напряжение смещения на входных электродах транзистора 0,4 В, амплитуда напряжения гармонического колебания 0,8 В. Рассчитайте спектральный состав отклика. Нарисуйте временную диаграмму отклика при отсутствии фильтра.
3.25 Вольтамперная характеристика нелинейного элемента аппроксимирована полиномом 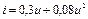 . На вход нелинейного элемента поданы два синусоидальные колебания частотой 96 кГц и 6 кГц, амплитудой соответственно
. На вход нелинейного элемента поданы два синусоидальные колебания частотой 96 кГц и 6 кГц, амплитудой соответственно 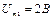 и
и 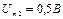 . Рассчитайте спектральный состав отклика для случая
. Рассчитайте спектральный состав отклика для случая 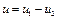 .
.
3.26 На вход нелинейного элемента, вольтамперная характеристика которого аппроксимирована полиномом 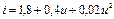 подается сумма гармонических колебаний
подается сумма гармонических колебаний 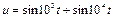 . Рассчитайте спектральный состав отклика нелинейного элемента и постройте спектральную диаграмму отклика.
. Рассчитайте спектральный состав отклика нелинейного элемента и постройте спектральную диаграмму отклика.
3.27 Вольтамперная характеристика нелинейного элемента аппроксимирована полиномом 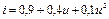 . На вход нелинейного элемента поданы гармонические колебания
. На вход нелинейного элемента поданы гармонические колебания 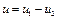 , причем
, причем 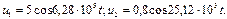 Рассчитайте спектральный состав отклика и постройте по результатам расчета спектральную диаграмму отклика.
Рассчитайте спектральный состав отклика и постройте по результатам расчета спектральную диаграмму отклика.
МОДУЛИРОВАННЫЕ СИГНАЛЫ
Аналоговая модуляция
Таблица 4.1 – Обозначение физических величин
| Наименование физической величины | Обозначение | Единицы измерения |
| Амплитуда несущего колебания | Am , Um , Im | В, Вольт; А, Ампер |
| Циклическая частота несущего колебания | 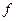
| Гц, Герц |
| Угловая частота несущего колебания | 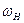
| рад/с, радиан в секунду |
| Амплитуда информационного (модулирующего) сигнала | Amu, Umu , Imu | В, Вольт; А, Ампер |
| Циклическая частота информационного (модулирующего) сигнала | 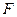
| Гц, Герц |
| Угловая частота информационного (модулирующего) сигнала | 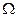
| рад/с, радиан в секунду |
| Коэффициент амплитудной модуляции | m | -- |
| Коэффициент пропорциональности | α | |
| Девиация частоты | Δf | Гц, Герц |
| Индекс частотной модуляции | Мчм | -- |
| Индекс фазовой модуляции | Мфм | -- |
| Функции Бесселя | Jk | -- |
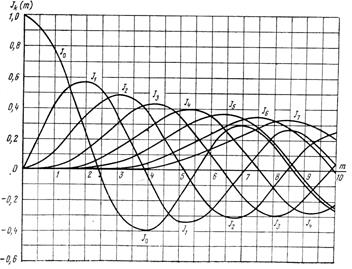
Рисунок 4.1 – Графики функций Бесселя
Примеры решения задач:
Задача 1. Составьте математическую модель амплитудно-модулированного (АМ) сигнала, постройте его спектральную диаграмму и определите ширину спектра АМ сигнала, если на вход модулятора подается модулирующее колебание частотой 3,3 кГц и амплитудной 0,4 В. Коэффициент амплитудной модуляции равен 24%, частота несущего колебания равна 88 кГц. Начальные фазы несущего и модулирующего колебаний равны нулю, 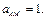
Дано: F =3,3 кГц Umu =0,4 В f н =88 кГц m =24%=0,24 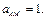
Решение: Математическая модель АМ сигнала согласно [1]имеет вид
S АМ ( t )= Um (1+ mcos Ω t ) cos ω н t
Угловые частоты определим по формуле 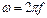 .
.
Амплитуду несущей рассчитаем, воспользовавшись формулой
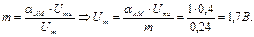
Тогда математическая модель АМ сигнала будет иметь вид
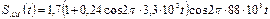
Ширину спектра АМ сигнала рассчитаем по формуле
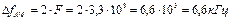
Построим спектральную диаграмму АМ сигнала. Для этого рассчитаем амплитуды и частоты боковых составляющих.
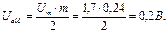
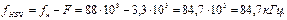
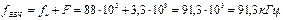
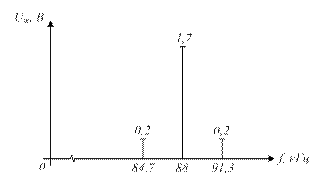
Задача 2. Дополните текст: «Отношение … … к частоте … … сигнала называется индексом частотной модуляции».
Решение: Согласно [2], «отношение девиации частоты частоте информационного сигнала называется индексом частотной модуляции»
Задачи для самостоятельного решения:
4.1 Дополните текст:«… … - это процесс изменения частоты … колебания по закону непрерывного … сигнала»..
4.2 Вставьте недостающие слова: «… … - это процесс изменения фазы … колебания по закону непрерывного … сигнала».
4.3 Какое выражение соответствует математической модели амплитудно-модулированного сигнала?
Варианты ответов:
а) Um(1+mcosΩt)cosω0t; б)Umsin(ω0 t - McosΩt);
в) Umcos(ω0t+∆φsinΩt); г) Umsinωt∙sinΩt.
4.4 Какое выражение соответствует математической модели частотно-модулированного сигнала?
Варианты ответов:
а) Um(1+mcosΩt)cosω0t; б)Umsin(ω0t-McosΩt);
в) Umsinωt∙sinΩt; г) Umcos(ω0t+∆φsinΩt).
4.5 Какое выражение соответствует математической модели фазомодулированного сигнала?
Варианты ответов:
а)Umsin(ω0t+∆ ωmcosΩt); б)Umcos(ω0t+∆φsinΩt);
в)Um(1+mcosΩt)cosω0t; г) Umsinωt∙sinΩt.
4.6 По какой формуле определяется ширина спектра амплитудно-модулированного сигнала?
Варианты ответов: а) 2Fmin; б) 2Fmax(1+M);
в) Fmax ; г) нет правильного ответа.
4.7 По какой формуле определяется ширина спектра частотно-модулированного сигнала?
Варианты ответов: а) 2Fmах; б) 2Fmax(1+M); в) Fmax ; г)2МFmaх.
4.8 Вставьте недостающие слова: «Модуляция – это один из способов согласования параметров … с параметрами …».
4.9 Вставьте недостающие слова: «Наибольшее отклонение частоты при модуляции называется …».
4.10 По какой формуле определяется индекс частотной модуляции?
Варианты ответов: а) 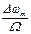 ; б)
; б) 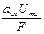 ; в)
; в) 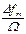 ; г) ачм Umu .
; г) ачм Umu .
4.11 Дополните текст: «При амплитудной модуляции ширина спектра модулированного сигнала равна … значению максимальной частоты … сигнала».
4.12 По какой формуле определяется девиация фазы при фазовой модуляции?
Варианты ответов: а) 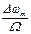 ; б)
; б) 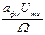 ; в)
; в) 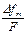 ; г) афмUmu.
; г) афмUmu.
4.13 Нарисуйте временную диаграмму амплитудно-модулированного сигнала, если на вход модулятора подан модулирующий сигнал (см. рисунок 4.2)
4.14 Нарисуйте временную диаграмму частотно-модулированного сигнала, если на вход модулятора подан модулирующий сигнал (см. рисунок 4.2)

Рисунок 4.2 − Временная диаграмма сигнала
4.15 Нарисуйте временную диаграмму амплитудно-модулированного сигнала с коэффициентом амплитудной модуляции равным 0,3. Модулирующий сигнал – гармоническое колебание.
4.16 Постройте спектральную диаграмму амплитудно-модулированного сигнала, временная диаграмма которого приведена на рисунке 4.3.

Рисунок 4.3− Временная диаграмма модулированного сигнала
4.17 Нарисуйте в примерном масштабе временную и спектральную диаграммы модулированного сигнала, если его математическая модель имеет вид 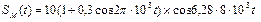 .
.
4.18 Уравнение модулирующего колебания 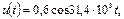 несущего колебания
несущего колебания 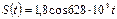 . Составьте математическую модель амплитудно-модулированного (АМ) сигнала, постройте спектральную диаграмму и рассчитайте ширину спектра АМ сигнала.
. Составьте математическую модель амплитудно-модулированного (АМ) сигнала, постройте спектральную диаграмму и рассчитайте ширину спектра АМ сигнала.
4.19 Составьте математическую модель амплитудно-модулированного (АМ) сигнала, постройте спектральную диаграмму и рассчитайте ширину спектра АМ сигнала, если на вход амплитудного модулятора подается несущее колебание частотой 112 кГц, амплитудой 2,1 В и модулирующий сигнал частотой 2,8 кГц и амплитудой 0,7 В. Начальные фазы несущего колебания и модулирующего сигналов принять равными нулю, 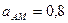 .
.
4.20 На вход амплитудного модулятора подан телефонный сигнал и несущее колебание частотой 104 кГц. Рассчитайте ширину спектра амплитудно-модулированного сигнала, постройте спектральную диаграмму.
4.21 На вход амплитудного модулятора подано гармоническое колебание частотой 6,3 кГц, амплитудой 10 мА и несущее колебание частотой 96 кГц и амплитудой 15 мА. Определите ширину спектра модулированного сигнала и амплитуду нижней боковой частоты.
4.22 Рассчитайте ширину спектра амплитудно-модулированного (АМ) сигнала, если несущее колебание частотой 564 кГц и амплитудой 3 В, а модулирующее колебание 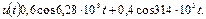 Определите амплитуды верхних боковых частот, если
Определите амплитуды верхних боковых частот, если 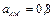 . Постройте спектральную диаграмму АМ сигнала.
. Постройте спектральную диаграмму АМ сигнала.
4.23 Рассчитайте спектр амплитудно-модулированного сигнала, если модулирующим сигналом является периодическая последовательность прямоугольных импульсов с параметрами из условия задачи 2.11. Частота несущего колебания 420 кГц, амплитуда-20 В, коэффициент 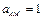 .
.
4.24 Измерения показали, что период несущего колебании амплитудно-модулированного сигнала с подавленной несущей равен 20∙10-6с, а период модулирующего колебания равен 0,5∙10-3с.Амплитуда несущего колебания равна 2 В, амплитуда модулирующего колебания равна 0,7 В. Рассчитайте спектральный состав АМ сигнала, постройте его спектральную диаграмму, запишите математическое выражение для спектра сигнала.
4.25 Задано аналитическое выражение АМ колебания: SAM ( t )=14(1+0,6 cos 104 t +0,7 cos 5∙103 t ) cos 106 t , В. Постройте спектральную диаграмму АМ сигнала, определите ширину спектра, составьте математическую модель модулирующего колебания, если αАМ=0,8.
4.26 Приведена спектральная диаграмма амплитудно-модулированного сигнала (рисунок 4.4). Составьте математическую модель модулирующего, несущего и модулированного колебаний.
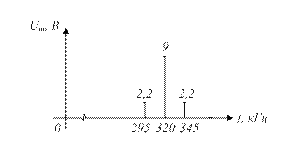
Рисунок 4.4 – Спектральная диаграмма АМ сигнала
4.27 Радиосвязь ведется на волне 47 м с использованием однополосной амплитудной модуляции (ОМ). Модулирующий сигнал занимает полосу частот 100…6000 Гц, амплитуда несущего колебания равна 100 В, коэффициент амплитудной модуляции равен 0,65. Определите наибольшую и наименьшую амплитуды модулированного сигнала, крайние частоты и ширину спектра модулированного сигнала, если выделяется нижняя боковая полоса частот. Составьте математическую модель ОМ сигнала.
4.28 Приведена математическая модель модулированного сигнала 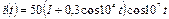 . Какой вид модуляции использован? Рассчитайте спектральный состав модулированного сигнала, по результатам расчета постройте спектральную диаграмму сигнала.
. Какой вид модуляции использован? Рассчитайте спектральный состав модулированного сигнала, по результатам расчета постройте спектральную диаграмму сигнала.
4.29 Определите длину волны несущего колебания, ширину спектра и амплитуды боковых составляющих модулированного сигнала 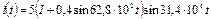 . Нарисуйте спектральную диаграмму модулированного сигнала.
. Нарисуйте спектральную диаграмму модулированного сигнала.
4.30 Рассчитайте коэффициент амплитудной модуляции, наименьшую и наибольшую амплитуды модулированного сигнала, нижнюю и верхнюю боковые частоты и ширину спектра модулированного сигнала, если частота несущего колебания 150 кГц, частота модулирующего сигнала 5 кГц, амплитуда несущего колебания 200 В, наибольший прирост амплитуды при модуляции 40 В, коэффициент 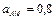 .
.
4.31 На вход амплитудного модулятора подан модулирующий сигнал 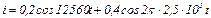 и несущее колебание частотой 96 кГц, амплитудой 600 мА. Постройте спектральную диаграмму амплитудно-модулированного сигнала, принять аАМ=0,8.
и несущее колебание частотой 96 кГц, амплитудой 600 мА. Постройте спектральную диаграмму амплитудно-модулированного сигнала, принять аАМ=0,8.
4.32 На выходе амплитудного модулятора формируется сигнал 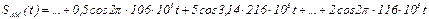 . Определите параметры составляющих модулированного сигнала, пропущенные по тексту (…). Рассчитайте ширину спектра и постройте спектральную диаграмму модулированного сигнала.
. Определите параметры составляющих модулированного сигнала, пропущенные по тексту (…). Рассчитайте ширину спектра и постройте спектральную диаграмму модулированного сигнала.
4.33 Дополните текст: «При … частотной модуляции ширина спектра модулированных колебаний практически равна … девиации частоты».
4.34 Дополните текст: «При … частотной модуляции ширина спектра модулированного сигнала практически равна … максимальной частоте модулирующего сигнала».
4.35 Измерения дали следующие результаты: амплитуда частотно-модулированного (ЧМ) сигнала равна 1 В, амплитуда модулирующего сигнала равна 0,1 В, несущая частота ЧМ сигнала 10 МГц, период модулирующего сигнала 12,5 мкс, крутизна модуляционной характеристики 32∙106 Гц/В. Запишите математическое выражение для ЧМ сигнала. Постройте спектральную диаграмму ЧМ сигнала.
4.36 Определите ширину спектра частотно-модулированного (ЧМ) сигнала и составьте уравнение несущего колебания, если радиопередатчик работает на волне 4,16 м, девиация частоты равна 50 кГц, максимальная частота модулирующего сигнала равна 15 кГц, амплитуда несущего колебания -100 В.
4.37 Девиация частоты частотно-модулированного (ЧМ) сигнала равна 50 кГц. Определите минимальную частоту модулирующего сигнала, при которой амплитуда спектральной составляющей ЧМ сигнала с частотой несущего колебания будет равна нулю.
4.38 Индекс частотной модуляции (ЧМ) равен 0,6, частота несущего колебания равна 56 МГц, амплитуда несущего колебания 15 В. Модулирующее напряжение изменяется по косинусоидальному закону, частота модулирующего сигнала 3,4 кГц, начальная фаза колебания 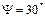 ,
, 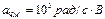 . Составьте математическую модель ЧМ сигнала. Постройте спектральную диаграмму. Определите ширину спектра модулированного сигнала и амплитуду модулирующего сигнала.
. Составьте математическую модель ЧМ сигнала. Постройте спектральную диаграмму. Определите ширину спектра модулированного сигнала и амплитуду модулирующего сигнала.
4.39 Найдите ширину спектра частотно-модулированного (ЧМ) сигнала, если 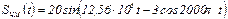 . Как изменится спектр ЧМ сигнала, если индекс частотной модуляции станет равным 2,4?
. Как изменится спектр ЧМ сигнала, если индекс частотной модуляции станет равным 2,4?
4.40 Приведена математическая модель модулированного сигнала 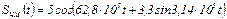 . Составьте математические модели несущего колебания и модулирующего сигнала. Определите циклическую частоту модулирующего сигнала, ширину спектра модулированного сигнала и период частоты несущего колебания
. Составьте математические модели несущего колебания и модулирующего сигнала. Определите циклическую частоту модулирующего сигнала, ширину спектра модулированного сигнала и период частоты несущего колебания 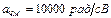 .
.
4.41 Найдите максимальную и минимальную мгновенные частоты, а также девиацию частоты частотно-модулированного сигнала, заданного аналитическим выражением :
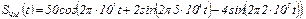
4.42 Составьте математическую модель частотно-модулированного сигнала, если радиопередающее устройство работает на волне 4 м, частота модулирующего сигнала 15 кГц, девиация частоты 50 кГц, амплитуда несущего колебания 75 В.
4.43 Рассчитайте длину волны радиостанции МВ ЧМ вещания, девиацию и индекс частотно-модулированного (ЧМ) сигнала, если полоса частот излучения радиостанции 72,95…73,05 МГц, максимальная частота модулирующего сигнала 15 кГц. Составьте математическую модель сигнала, если амплитуда несущего колебания равна 120 В.
4.44 Входная цепь радиоприемного устройства содержит колебательный контур, настроенный на частоту 68 МГц, добротность контура равна 40. Можно ли использовать этот контур для приема частотно-модулированного сигнала, частота которого меняется по закону 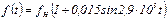 ?
?
4.45 Определите индекс частотно-модулированного сигнала, промодулированного частотой 800 кГц, если несущая частота 70 МГц, а максимальное значение частоты модулированного сигнала 71,5 МГц.
4.46 Постройте спектральную диаграмму частотно-модулированного сигнала с амплитудой 20 В и индексом 2,4.
4.47 Амплитуда сигнала на выходе передатчика частотно-модулированных сигналов в отсутствие модулирующего колебания равна 200 В. Измерения показали, что при подаче гармонического модулирующего колебания амплитуда несущего колебания становится равной 40 В. Определите индекс частотной модуляции. Можно ли полагать, что в описываемых условиях реализована узкополосная модуляция?
4.48 Радиостанция излучает фазомодулированный сигнал, индекс модуляции равен 12. Найдите пределы, в которых изменяется мгновенная частота сигнала, если частота несущего колебания 80 МГц, частота модулирующего сигнала 12 кГц.
4.49 Задан фазомодулированный сигнал с частотой модуляции 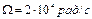 . При какой девиации частоты в спектре этого сигнала будут отсутствовать составляющие сигнала на частотах
. При какой девиации частоты в спектре этого сигнала будут отсутствовать составляющие сигнала на частотах 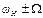 ?
?
4.50 Частота фазомодулированного колебания изменяется по закону 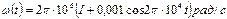 . Составьте аналитическое выражение для этого колебания, если его амплитуда равна 10 В.
. Составьте аналитическое выражение для этого колебания, если его амплитуда равна 10 В.
Дата: 2019-03-05, просмотров: 812.