Методика обработки экспериментальных данных единая и проводится в следующих случаях:
· при обработке результатов измерений;
· при статистическом анализе точности и стабильности технологического процесса;
· при определении погрешности измерения нестандартизованных средств измерений (НСИ);
· при аттестации приборов и контрольно - измерительных приспособлений.
Будем рассматривать задачу на конкретном примере.
Дано: при обработке 100 валов под размер 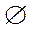
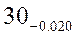 получились следующие результаты измерения представленные в протоколе испытаний. При этом валы измерялись рычажной скобой (пределы измерения 25
получились следующие результаты измерения представленные в протоколе испытаний. При этом валы измерялись рычажной скобой (пределы измерения 25  50 мм, цена деления 0.002 мм,
50 мм, цена деления 0.002 мм, 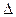 lim=
lim= 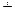 3 мкм).
3 мкм).
Протокол испытаний
| Размеры (мм) | Отклонения (мкм) | ||||
| 30.002 | max | +2 | max | ||
| 30.000 |
| 0 |
| ||
| 29.998 |
| - 2 |
| ||
| 29.975 | min | - 25 | min | ||
| 29.978 |
| - 22 |
| ||
| 29.990 |
| -10 |
| ||
| 29.992 |
| -8 |
| ||
| . . . . . . . . . . . . . .и т.д. всего 100 результатов измерений. | |||||
Требуется: определить закон распределения размеров, построить практическую (эмпирическую) и теоретическую кривые распределения.
Решение задачи.
1. Из всех результатов измерения (n = 100) выбираем max и min значения и определяем их разность (размах результатов), т.е. зону рассеивания действительных размеров (V):
V=30.002-29.975=0.027 мм, т.е. 27 мкм.
2. Задаемся величиной разряда C 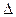 =3мкм и количеством интервалов (разрядов). Рекомендуется нечетное количество интервалов (k) не менее 5. В нашем случае удобно взять k=9 (27:3=9). Общее количество интервалов определяется k+1.
=3мкм и количеством интервалов (разрядов). Рекомендуется нечетное количество интервалов (k) не менее 5. В нашем случае удобно взять k=9 (27:3=9). Общее количество интервалов определяется k+1.
3. Подсчитаем количество результатов измерения в каждом интервале (частоту повторений ni) и данные заносим в таблицу. Значения интервалов можно выражать в предельных размерах и в отклонениях от номинального значения (мкм). Для дальнейших расчетов удобнее пользоваться значениями отклонений.
Для заполнения без ошибок таблицы «Определение погрешности обьекта», удобнее составить статистический ряд из результатов измерений. При этом записать значение в мкм (т.е. значение отклонений с учетом знаков) от наименьшего до наибольшего и разбить полученный ряд (так называемую упорядоченную статистическую совокупность) на интервалы.
Например:
| отклонения в виде статистического ряда | -25,-24,-23 | -22,-22,-22,-21,-20,-20 | -19,-18 и т.д. | +1 | +4 |
| номер интервала в таблице 6.1 | 1 | 2 | и т.д. | 9 | 10 |
| частота повторений в интервале | 3 | 6 | 1 | 1 |
4. Находим среднее значение интервала 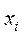 и записываем в таблицу 6.1.
и записываем в таблицу 6.1.
5. Определяем произведения n 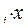 i и n
i и n 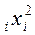
 и результаты заносим в таблицу
и результаты заносим в таблицу
6. Определяем среднее выборочное арифметическое отклонение случайных погрешностей 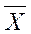 по формуле:
по формуле:
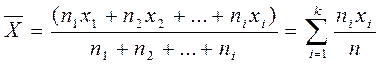
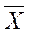 = [(-23,5) × 3 + (-20,5) × 6 + (-17,5) × 13 +. . . + 3,5 × 1)] : 100
= [(-23,5) × 3 + (-20,5) × 6 + (-17,5) × 13 +. . . + 3,5 × 1)] : 100
7. Определяем среднее выборочное квадратическое отклонение по формуле:
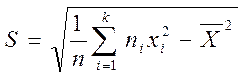
S можно вычислить и по другим формулам, но при этом выше трудоемкость. При расчете S по этой формуле погрешность вычисления составляет 1,6% [10].
Таблица 6.1
Определение погрешности объекта
| Номер интервала | Значение интервала | Частота повторений в интервале ni | Среднее значение интервала xi | Математическая обработка данных | |
| nixi | nixi2 | ||||
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 2 3 4 5 6 7 8 9 10 | -25…-22 -22…-19 -19…-16 -16…-13 -13…-10 -10…-7 -7…-4 -4…-1 -1…+2 +2…+5 | 3 6 13 17 26 16 12 5 1 1 | -23,5 -20,5 -17,5 -14,5 -11,5 -8,5 -5,5 -2,5 +0,5 +3,5 | Подсчи-таем с учетом знака | |
8. Конечным итогом обработки результатов измерения является определение 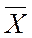 и S. Дальнейшая обработка результатов связана с решением поставленной задачи. Как правило, из данных таблицы определяют моду (
и S. Дальнейшая обработка результатов связана с решением поставленной задачи. Как правило, из данных таблицы определяют моду ( 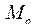 = -11.5), частоту моды (nMo=26),
= -11.5), частоту моды (nMo=26), 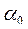 -меру асимметрии, и
-меру асимметрии, и 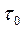 - эксцесс:
- эксцесс:
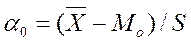 ;
; 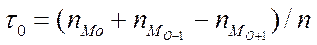 .
.
По полученным величинам делают заключение о характере кривой распределения и соответствия практической кривой предполагаемому закону распределения. Для предварительного вывода о законе распределения строят гистограмму распределения результатов измерения.
9. Строится гистограмма (в произвольном масштабе);
10. В случае, если а похожа на кривую Гаусса строится практическая кривая и сравнивается с соответствующими законами распределения;
11. Практическая кривая сравнивается с теоретической кривой. С этой целью их строят в одном масштабе, применяя метод Апарина и Городецкого (метод масштабных коэффициентов).
12. Сопоставление кривых проводят по значениям 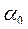 ,
, 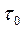 , сравнивая их с нормативными значениями, а также по критерию согласия А.Н.Колмогорова – значению Р(λ), сравнивая его с табличными значениями.
, сравнивая их с нормативными значениями, а также по критерию согласия А.Н.Колмогорова – значению Р(λ), сравнивая его с табличными значениями.
Подробная методика решения данной задачи дана в литературе [9,10,13]. Кроме того, студенты будут выполнять лабораторные работы, связанные с обработкой результатов измерений по рассмотренной методике, т.е. ознакомятся практически.
Дата: 2019-02-19, просмотров: 408.