Зависимость между числовыми значениями случайной величины и вероятностью их появления устанавливается законом распределения.

В результате обработки экспериментальных данных мы получаем эмпирические (практические) кривые, которые примерно соответствуют какому-либо теоретическому закону распределения. Рассмотрим наиболее часто встречающиеся в машиностроении и метрологическом обеспечении производства законы распределения (рис. 5.1):

1- закон Гаусса; 2- закон Максвелла; 3- закон Симпсона; 4 – закон равной вероятности; 5 – закон Вейбулла; 6 – закон нормального модуля упрощенного

- закон Гаусса (1). Закон нормального распределения. Этому закону подчиняется рассеивание значений случайной величины, изменение которой зависит от большого числа факторов, ни один из которых не является доминирующим. Это наиболее часто встречающийся на практике закон распределения. Закону Гаусса с некоторым приближением может подчиняться рассеивание погрешностей изготовления или измерения линейных и угловых размеров, погрешностей массы деталей, величин твердости и других физико-механических свойств материалов.

- закон Максвелла (2). Закон эксцентриситетов, которому может соответствовать рассеивание значений несоосности, радиального и торцевого биения, отклонении от параллельности, отклонении от перпендикулярности двух плоскостей (или оси и плоскости) и тому подобных величин, которые могут иметь только положительные значения.

- закон Симпсона (3). Закон равнобедренного треугольника, этому закону подчиняются случайные величины, на которые оказывают суммарное давление два резко доминирующих фактора.

- закон равной вероятности (4). Закон прямоугольника, он характерен для случайных величин, на которые оказывает влияние резко доминирующий фактор, равномерно изменяющийся в пространстве или во времени, например износ режущего инструмента.                    

- закон Вейбулла (5). Экспоненциальный закон, характеризующий периоды безотказной работы систем, станков, приборов, автоматических линий.

- закон нормального модуля упрощенного (6). Ему, как правило, подчиняются угловые отклонения, шаги резьб и зубчатых колес, отклонения от круглости.

Характеристики теоретического распределения

И их эмпирические аналоги

 Кривые распределения характеризуются статистическими характеристиками (для дискретных величин) или параметрами распределения (для непрерывных величин).

Результаты измерений в значительной степени сконцентрированы вокруг истинного значения измеряемой величины, и по мере приближения к нему элементы вероятности их появления возрастают. Характеристикой места группирования случайной величины – результата измерений - является математическое ожидание M(x). При отсутствии систематических погрешностей, при анализе рассеивания размеров деталей, обрабатываемых на станке, математическое ожидание можно рассматривать как размер, на который был настроен станок. Математическое ожидание не определяет степень рассеивания возможных значений погрешности около среднего значения. Для полной характеристики распределения погрешности применяют центральные моменты.

Одним из центральных моментов является дисперсия D(x), характеризующая рассеивание случайных величин вокруг математического ожидания.

В качестве характеристики рассеивания также используют среднее квадратическое отклонение результатов измерения .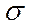

D (x) = .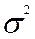

Для более подробного описания распределения используют коэффициент асимметрии 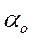, характеризующий асимметрию или скошенность распределения, и эксцесс 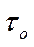, служащий для характеристики плосковершинности или островершинности (рис. 5.2).

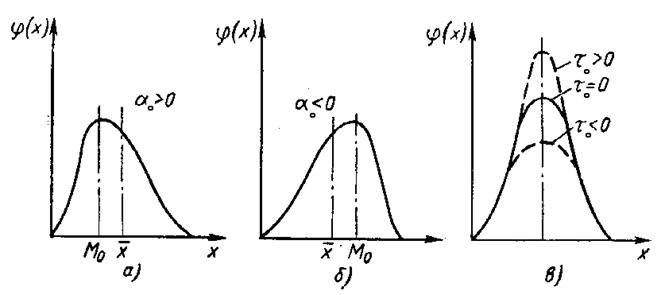
Рис. 5.2 - Кривые распределения с уклонениями от нормального закона распределения:

а и б – асимметричные; в – остро- и плосковершинные

На рис.5.3 представлена кривая нормального распределения и поля рассеивания (зоны рассеивания) при различных количествах . Зону рассеивания (V) принято рассматривать в пределах  n-количества . Площадь, ограниченная кривой нормального распределения и осью абсцисс в зоне , принимается равной единице (100 %) и при совпадении начала координат с центром группирования выражается интегралом. Подинтегральная функция является четной, кривая является симметричной.  

В теории вероятностей часто используют коэффициент риска Z = x / 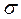 , причем, x - значение расстояния от центра группирования до интересующего нас значения по оси абсцисс. Функция Ф(Z) носит название нормированной функции Лапласа. Имеются специальные таблицы, в которых приведены значения интеграла Ф(Z) при различных значениях коэффициента риска. С помощью этих таблиц в машиностроении решается ряд задач, требующих применения интегральной теоремы Лапласа, таких как определение количества деталей из партии, определение процента исправимого и неисправимого брака.

Но при решении практических задач следует задаваться более конкретной зоной рассеивания. На рис.5.3. представлены площади, ограниченные кривой Гаусса и рассматриваемые в зонах различного количества - .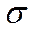

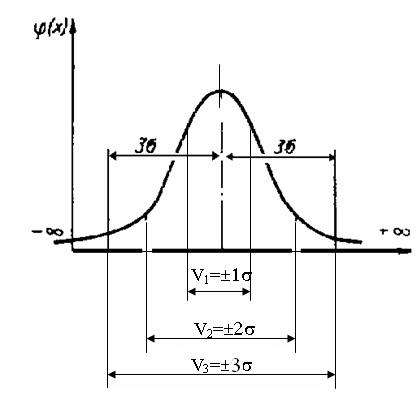
Рис. 5.3 - Зоны рассеивания при различных количествах s.

Этот рисунок можно рассматривать следующим образом:

- в зоне 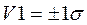 содержится 68% всех результатов (значений случайной величины);

- в зоне 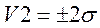  содержится  95%  всех  результатов,  т.е.  вероятность  равна 0,95;

- в зоне 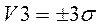 содержится 99.73% всех результатов;

- в зоне 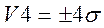 содержится 99.81% всех результатов;

- в зоне 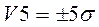 содержится 99,87% всех результатов и.т.д.

 Зону 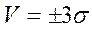 принимают за практически предельную зону рассеивания случайной величины, при этом вероятность выхода случайной величины за пределы значений  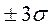составляет 0,27%. Однако, при решении задач по аттестации контрольно-измерительных приспособлений для массового и крупносерийного производства и выборе средств измерения для этих же типов производств зона рассеивания рассматривается в пределах 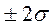, при этом вероятность выхода случайной величины за пределы зоны составляет 5%.

Ранее рассмотренным характеристикам теоретического распределения M(x), 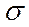, D(x) следует дать их эмпирические аналоги, т.е. те, которые будут получены в результате обработки результатов эксперимента. К ним относятся

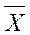 - выборочное среднее арифметическое значение величин (действительных размеров, отклонений, погрешностей); S - выборочное среднее квадратическое отклонение; S² - квадрат среднего арифметического выборочного отклонения.

Размерности 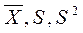 совпадают с размерностями случайных величин, для которых они определены. Чем меньше величина S, тем выше точность изготовления (или измерения), т.е. тем меньше величина случайных погрешностей изготовления (измерения). Поэтому параметр S используют в качестве меры точности метода измерения при повторных измерениях одной и той же величины.

Формулы для определения 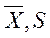 будут приведены в разделе 6.

Формулы, по которым определяются характеристики эмпирического распределения, учитывают объем выборки. Поэтому первое, что следует сделать при проведении экспериментальных исследований - это запланировать объем выборки.

Малой выборкой считается выборка, объем которой не превышает 20 единиц. Если объем выборки больше 25-30 единиц, она считается большой. При анализе производственных процессов обычно применяются большие выборки, состоящие из 50-100 единиц продукции. При контроле стабильных (отрегулированных) технологических процессов - малые выборки объемом 10-25 единиц.