1.7.1 Диаграмма перемещения поршня 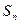 в зависимости от угла поворота  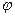кривошипа

Диаграмма строиться по данным таблицы 2 для одного полного оборота кривошипа на угол 360^º. Углы поворота кривошипа 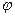 откладываем по оси абсцисс. Приняв длину отрезка 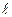, изображающего угол 360^º  за 120 мм. определим масштаб углов, рад/мм.

,

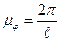(12)

,

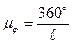(13)

,

,

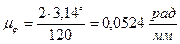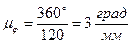Отрезок 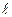 делим на 12 равных частей. Обозначим точки деления 0, 1, 2, …12. Каждое деление 0-1, 1-2, и т.д. Соответствует углу поворота кривошипа на 30^º.

Так как кривошип вращается равномерно и величина угла 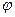 поворота кривошипа пропорциональна времени  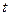вращения, то по оси абсцисс можно также откладывать и время  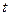в масштабе 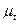, , 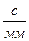величина которой определяется из формулы:

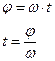
(14)

,

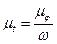(15)

,

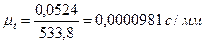Из точек деления 0, 1, 2 и т.д., взятых на оси абсцисс восстанавливаем к ней перпендикуляры, на которых откладываем отрезки 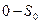, , 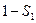 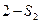и т.д. В определенном масштабе  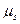эти ординаты отражают перемещение поршня (точки В) из исходного положения (точка 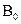) в положение соответствующее номеру деления. Масштаб  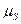определим исходя из наибольшего перемещения поршня.

Оно соответствует шестому положению поршня при угле поворота 180^º и равно 0,080 м. Примем величину наибольшего ординате на чертеже 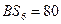 мм.

Тогда:

, .

,

.

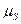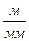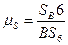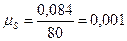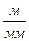Величину любой ординаты на чертеже, мм, находим из выражения:

,

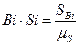где 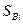 берем из таблицы 2.

Соединяя последовательно плавной кривой точки 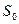, , 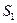 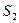и т.д. получим график функции 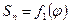. (Рисунок 7а)

1.7.2 Диаграмма скорости поршня .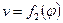

Построение диаграммы производим приближенным графиком дифференцированием кривого 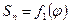 способом проведения хорд.

Истинная скорость поршня 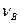 в точке В определяется тангенсом угла наклона касательной в требуемой точке диаграммы  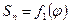к оси абсцисс. В определенном масштабе тангенс угла наклона выражает величину скорости

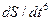. Так как точное проведение касательных к кривой является сложной и трудоемкой задачей вместо истинных скоростей в каждой точке определим средние скорости на элементарных участках .

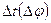Точки 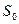, , 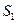 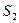и т.д. соединяем хордами 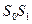, , 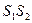и т.д. На продолжении оси абсцисс влево от начала координат откладываем полюсное расстояние  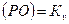мм. Приме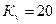м  мм.

Из полюса Р проводим лучи, параллельные хордам 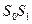,  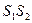и т.д. до пресечения с осью ординат. Отрезки 0-1, 1-2, 0-3 отсекаемые лучами на оси ординат, в масштабе 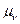, , 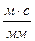изображают средние скорости на участках 0-1, 1-2 и т.д. При оси абсцисс откладываем углы поворота кривошипа в тех же масштабах  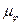и 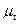, что и на диаграмме 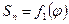. На делениях 0-1, 1-2, 2-3 и т.д. строим прямоугольники, высоты которых выражают средние скорости на участках и равны соответствующим отрезкам 01, 02, 03 и т.д. отмеченными на оси ординат лучами. Получилась ступенчатая форма диаграммы. Так как в действительности скорость поршня изменяется плавно и непрерывно, через середины уступов приводим плавную кривую, которая с достаточной точностью изображает изменение скорости.

Масштаб

,

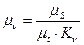(16)

.

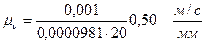(16)

Для сравнения величины скоростей, полученных графическим дифференцированием, с величиной скоростей, определенных способом планов, строим на этой же системе координат штриховыми линиями кривую 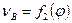 по данным, приведенным в таблице 2. (Рисунок 7б)

1.7.3. Диаграмма ускорений поршня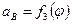

Построение кинематической диаграммы ускорений производится графическим дифференцированием диаграммы 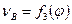 аналогично построению диаграммы 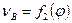. Масштаб  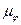и 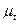 те же, что и в описанных выше диаграммах. Масштаб 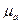, , 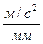определяется по формуле:

,

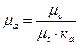(17)

где .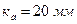

.

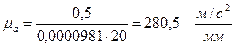Для сравнения в этой же системе координат построим штриховыми линиями график функции 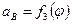 по данным, приведенным в таблице 2.