Выборочное среднее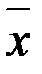 
– среднее арифметическое всех значений выборки, находится по формуле
.
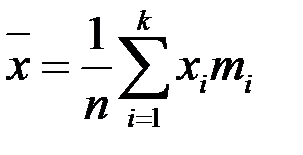Выборочная дисперсия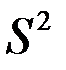 
вычисляется по формуле
.
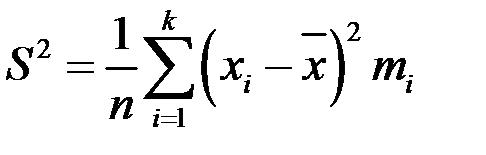Выборочное СКО вычисляется по формуле
.
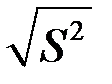Исправленная выборочная дисперсия вычисляется по формуле
.
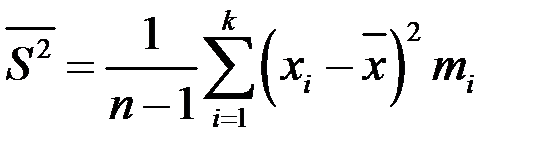Исправленное выборочное СКО вычисляется по формуле
.
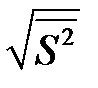Для группированной выборки формулы примут вид:
, 
, 
,
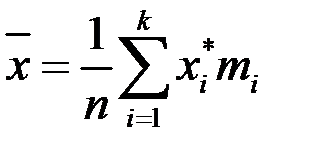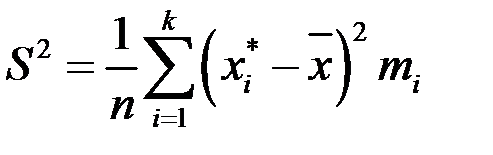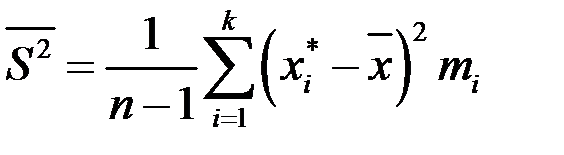где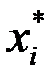 
– средняя точка интервала группированного ряда.
Доверительным интервалом называют интервал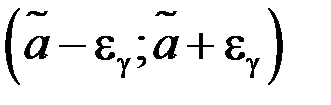 
, который покрывает неизвестный параметр а с заданной вероятностью g; здесь 
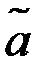– оценка параметра а, концы 
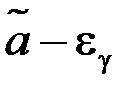и 
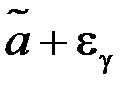– доверительные границы (они оценивают возможную погрешность), число g – доверительная вероятность или надежность. Число 
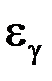характеризует точность оценки.
Доверительный интервал для математического ожидания при большом объеме выборки и неизвестном среднем квадратическом отклонении выражается формулой
,
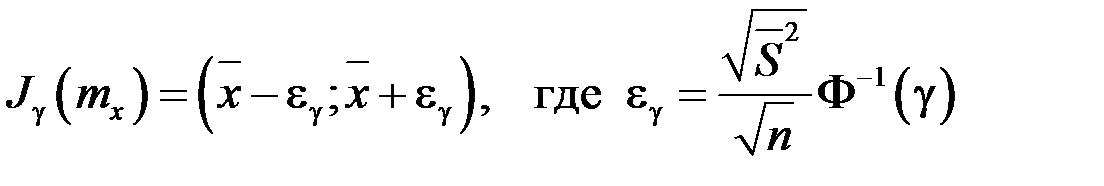где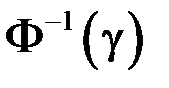 
– функция, обратная функции Лапласа 
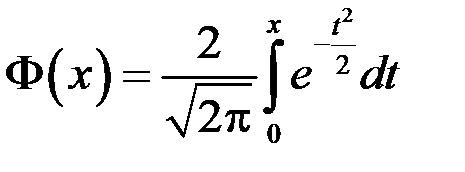(приложение 1), т.е. такое значение аргумента в таблице функции Лапласа, для которого функция Лапласа равна g.
Замечание. Если использовать таблицу значений функции Лапласа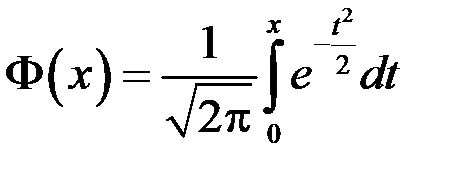 
, то точность оценки находится по формуле 
.
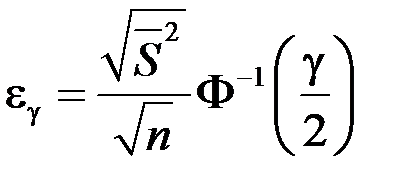Проверка статистической гипотезы о нормальном законе распределения генеральной совокупности с помощью критерия Пирсона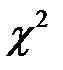 
Постановка задачи. Относительно некоторой генеральной совокупности Х высказывается гипотеза Н (о возможных значениях числовых характеристик, о виде закона распределения…) которую называют статистической гипотезой. Из этой генеральной совокупности извлекается выборка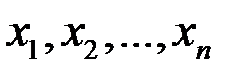 
. Требуется указать правило, при помощи которого можно было бы по каждой данной выборке решить вопрос о том, следует ли отклонить гипотезу Н или принять ее.
Нулевой гипотезой (основной) называют основную выдвигаемую гипотезу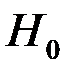 
.
Конкурирующей (альтернативной) называют гипотезу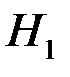 
, которая противоречит нулевой гипотезе 
.
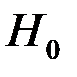Для проверки нулевой гипотезы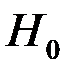 
используют специально подобранную случайную величину, которая рассчитывается по экспериментальной выборке, точное или приближенное распределение которой известно. Эту случайную величину К называют статистическим критерием.
Зная закон распределения К можно определить вероятность попадания К в любой интервал, т.е.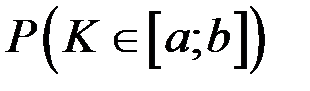 
для любых значений а и b.
Обозначим: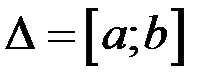 
.
Уровнем значимости a называют условное достаточно малое значение вероятности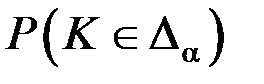 
, соответствующее практически невозможному событию 
. При этом область 
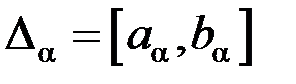называют критической областью.
Областью допустимых значений считают область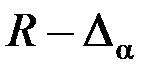 
, так как 
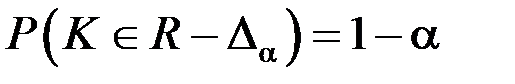достаточно велика при малых a.
Итак: при выбранном значении a для данной гипотезы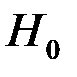 
известна критическая область 
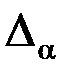, в которую с вероятностью 
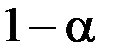критерий К попасть не должен.
Если вычисленный по выборке критерий К оказался в критической области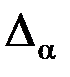 
, говорят о несоответствии гипотезы 
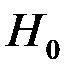фактическим данным, т.е. об отсутствии оснований принять гипотезу 
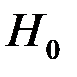. Если критерий К оказался вне критической области 
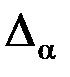, говорят о соответствии гипотезы фактическим данным, т.е об отсутствии оснований отвергать гипотезу 
.
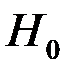При статистической проверке правильности выдвигаемой гипотезы могут быть допущены ошибки двух родов: ошибка первого рода состоит в том, что гипотеза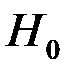 
отвергнута, а она верна; ошибка второго рода состоит в том, что гипотеза 
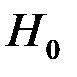принята, а она не верна.
Критерием согласия называют критерий проверки статистической гипотезы о предполагаемом законе неизвестного распределения СВ.
Критерий согласия Пирсона (критерий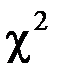 
).
Пусть выдвигается простая гипотеза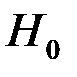 
, полностью определяющая вид функции распределения 
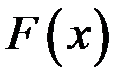исследуемой СВ Х. При этом имеется выборка достаточно большого объема, которой соответствует определенный статистический ряд.
В качестве критерия проверки справедливости гипотезы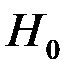 
выбирается СВ:
,
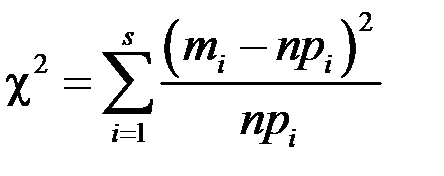где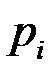 
– теоретические относительные частоты появления величины 
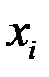, вычисленные в предположении гипотезы 
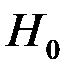по известной плотности распределения вероятностей 
; 
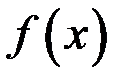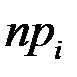– теоретические абсолютные частоты появления 
.
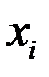Эта величина при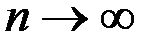 
распределена по закону 
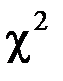с r степенями свободы
,
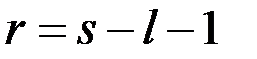где s – число различных значений СВ Х (количество интервалов группированной выборки), l – число параметров предполагаемого закона распределения.
Распределение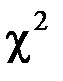 
не обладает симметрией, поэтому критическая область выбирается односторонней 
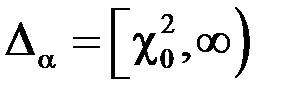, значение 
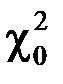полностью определяются по уровню значимости a и данному значению 
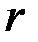по таблице распределения 
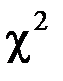(приложение 2).
Критерий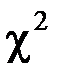 
использует тот факт, что случайная величина 
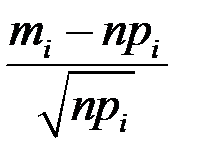имеет распределение, близкое к нормальному 
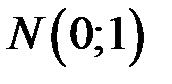. Чтобы это утверждение было достаточно точным, необходимо, чтобы для всех интервалов группированного статистического ряда выполнялось условие 
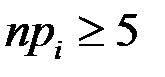. Если в некоторых интервалах это условие не выполняется, то их следует объединять с соседними. Так как после объединения остается меньше интервалов, то число степеней свободы следует вычислять, используя число вновь полученных интервалов.
Пример
Результаты измерений некоторой физической величины представлены в таблице:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 
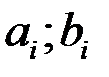
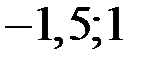
| 1;3,5 | 3,5;6 | 6;8,5 | 8,5;11 | 11;13,5 | 13,5;16 | 16;18,5 |
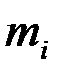
| 3 | 8 | 14 | 27 | 20 | 16 | 7 | 5 |
1. Найти функцию распределения выборки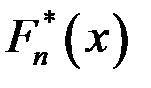 
и построить ее график.
2. Построить гистограмму относительных частот.
3. Найти числовые характеристики выборки: выборочное среднее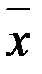 
и исправленную выборочную дисперсию 
.
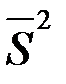4. Используя функцию Лапласа, построить доверительный интервал для математического ожидания, соответствующий доверительной вероятности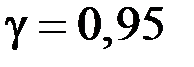 
.
5. С помощью критерия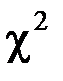 
(Пирсона) проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости 
.
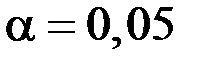Решение
Объем выборки 
, длина интервала 
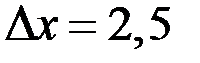. Для нахождения эмпирической функции распределения 
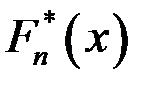, построения гистограммы относительных частот и вычисления числовых характеристик выборки дополним заданную таблицу следующими строками: строкой, в которой расположим средние точки 
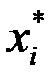каждого интервала, строкой относительных частот 
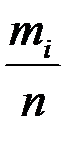, строкой накопленных относительных частот 
и строкой, в которой вычислим высоты столбиков гистограммы относительных частот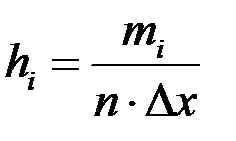 
.
Таблица 1
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
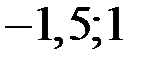
| 1;3,5 | 3,5;6 | 6;8,5 | 8,5;11 | 11;13,5 | 13,5;16 | 16;18,5 |
|
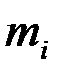
| 3 | 8 | 14 | 27 | 20 | 16 | 7 | 5 |
| 
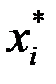
| 2,25 | 4,75 | 7,25 | 9,75 | 12,25 | 14,75 | 17,25 |
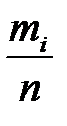
| 0,03 | 0,08 | 0,14 | 0,27 | 0,2 | 0,16 | 0,07 | 0,05 |
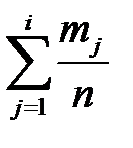
| 0,03 | 0,11 | 0,25 | 0,52 | 0,72 | 0,88 | 0,95 | 1 |
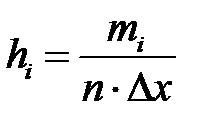
| 0,012 | 0,032 | 0,056 | 0,108 | 0,08 | 0,064 | 0,028 | 0,02 |
1. Эмпирическая функция распределения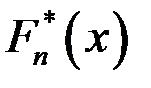 
определяется по значениям накопленных относительных частот, которые расположены в шестой строке таблицы 1. Эта функция имеет скачки в точках 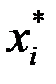– серединах интервалов группированного статистического ряда.
Аналитическое выражение эмпирической функции распределения имеет вид:
.
График эмпирической функции распределения 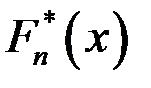изображен на рис. 1.
|
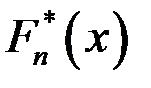
1 0,95 0,88
0,72
0,52
0,25
0,11 0,03 |
-0,25 2,25 4,75 7,25 9,75 12,25 14,75 17,25 х
Рис. 1
2. Построим гистограмму относительных частот, для этого на каждом интервале группированной выборки строим столбики, высоты которых вычислены в седьмой строке таблицы 1. График гистограммы изображен на рис. 2.
| 0 |
0,108
0,08
0,064
0,032 0,028
0,02
0,012
Рис. 2
3. Найдем числовые характеристики выборки. Выборочное среднее находим по формуле 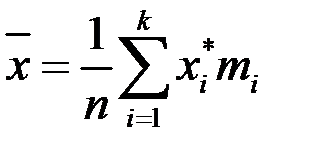, в нашем случае
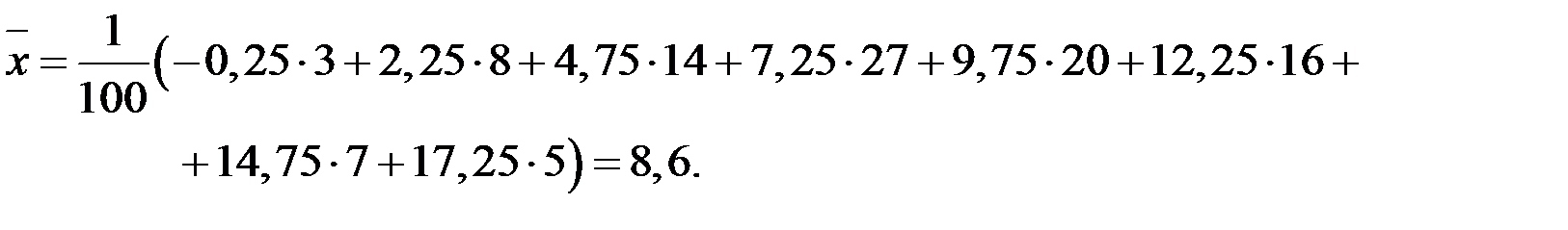
Исправленную выборочную дисперсию находим по формуле 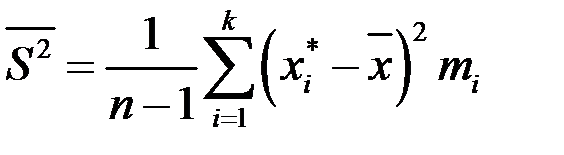, в нашем случае
.
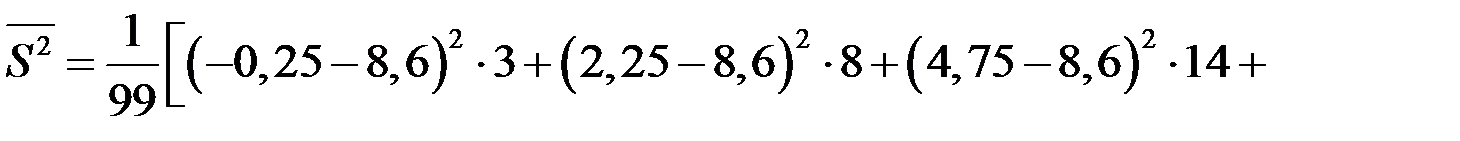
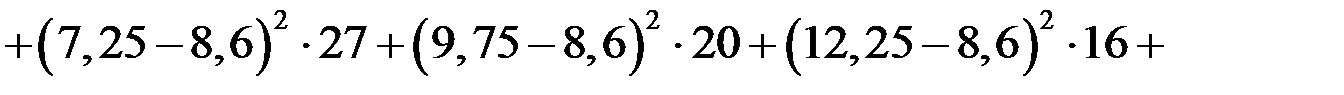
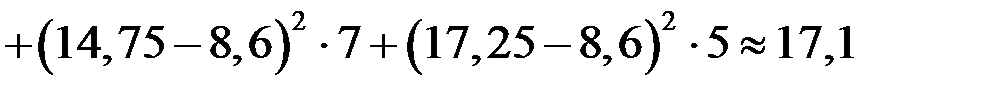4. При большом объеме выборки доверительный интервал для математического ожидания имеет вид
.
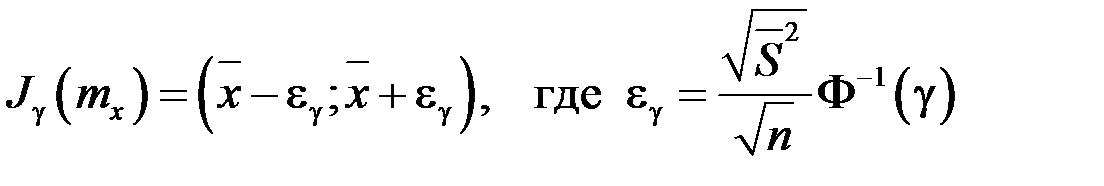Используя таблицу значений функции Лапласа (приложение 1) находим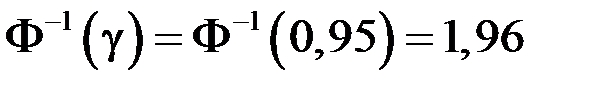 
.
Вычислим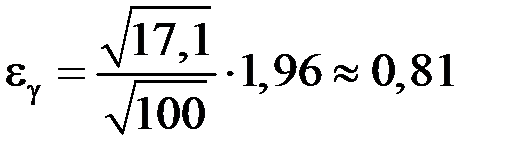 
, тогда доверительный интервал для математического ожидания имеет вид
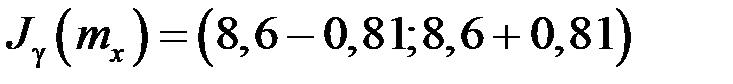
или
.
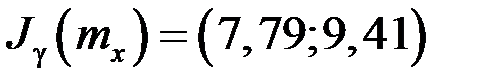5. Выдвигаем простую гипотезу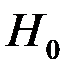 
о нормальном распределении генеральной совокупности. В качестве критерия проверки справедливости гипотезы выбирается случайная величина
,
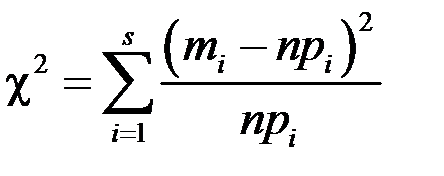где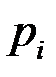 
находятся по формуле вероятности попадания случайной величины в интервал в предположении гипотезы о нормальном законе
,
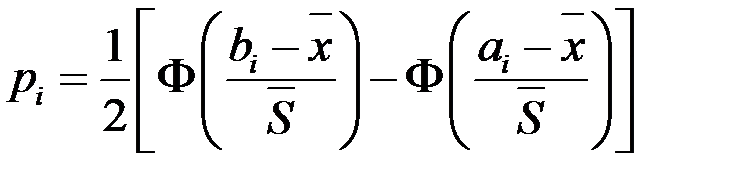где 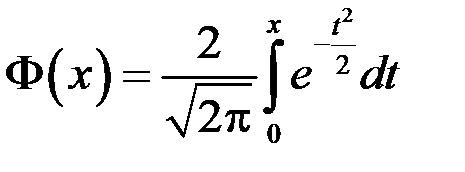– функция Лапласа.
Замечание. Если использовать таблицу значений функции Лапласа 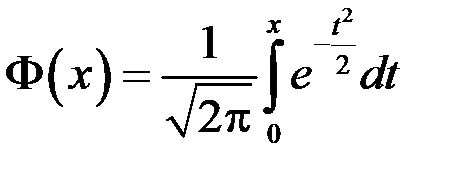, то вероятности попадания случайной величины в интервал в предположении гипотезы о нормальном законе распределения находится по формуле 
.
Для соблюдения условия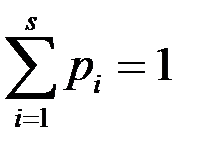 
полагают 
, 
.
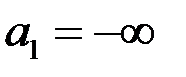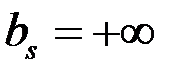Для вычисления критерия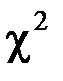 
составим расчетную таблицу:
Таблица 2
| I | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
|
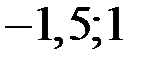
| 1;3,5 | 3,5;6 | 6;8,5 | 8,5;11 | 11;13,5 | 13,5;16 | 16;18,5 |
|
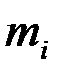
| 3 | 8 | 14 | 27 | 20 | 16 | 7 | 5 |
|
|
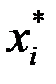
| 2,25 | 4,75 | 7,25 | 9,75 | 12,25 | 14,75 | 17,25 |
| 1 | 3,5 | 6 | 8,5 | 11 | 13,5 | 16 |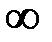 
|
| 
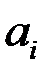
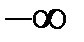
| 1 | 3,5 | 6 | 8,5 | 11 | 13,5 | 16 |
| 
| 
| 
| 
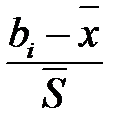
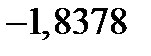
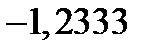
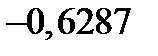
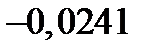
| 0,5803 | 1,1849 | 1,7895 |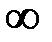
|
|
| 
| 
| 
| 
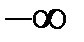
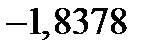
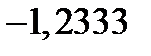
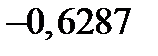
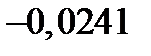
| 0,5803 | 1,1849 | 1,7895 |
| 
| 
| 
| 
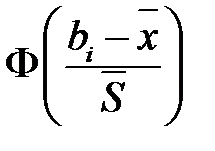
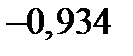
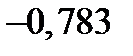
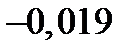
| 0,438 | 0,764 | 0,926 | 1 |
| 
|
|
|
|
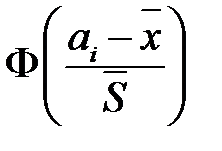
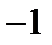
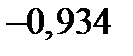
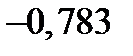
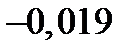
| 0,438 | 0,764 | 0,926 |
| 0,033 | 0,0755 | 0,1565 | 0,2255 | 0,2285 | 0,163 | 0,081 | 0,037 |
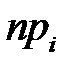
| 3,3 | 7,55 | 15,65 | 22,55 | 22,85 | 16,3 | 8,1 | 3,7 |
| 10,85 | 15,65 | 22,55 | 22,85 | 16,3 | 11,8 | |||
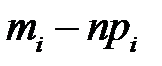
| 0,15 |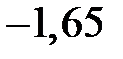 
| 4,45 |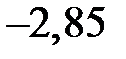 
| 
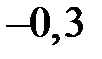
| 0,2 | ||
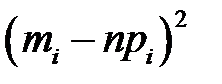
| 0,0225 | 2,7225 | 19,8025 | 8,1225 | 0,09 | 0,04 | ||
| 0,0020 | 0,1739 | 0,8781 | 0,3554 | 0,0055 | 0,0033 |
Находим сумму элементов 11-ой и 12-ой строк таблицы 2, получаем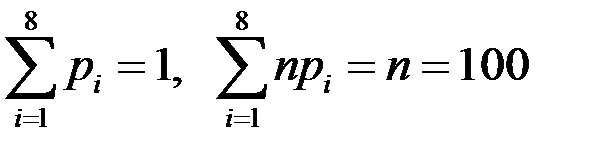 
.
Критерий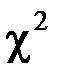 
равен сумме элементов последней строки таблицы 12:
.
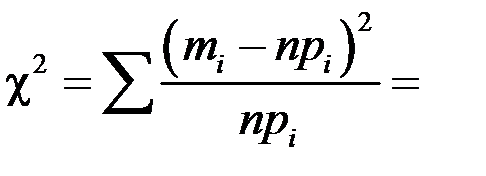
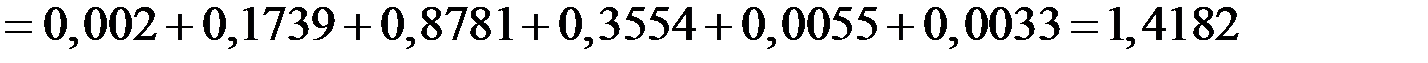Находим критическую область 
. Так как уровень значимости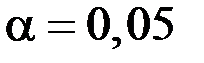 
по условию, число степеней свободы 
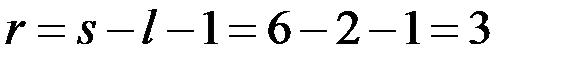, то согласно таблице распределения 
- 
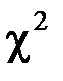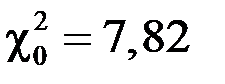, критическая область имеет вид 
.
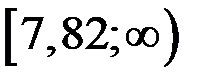Так как критерий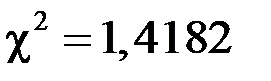 
не попал в критическую область 
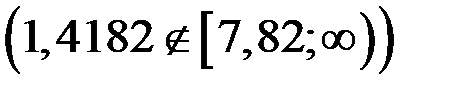, то нет оснований отвергать гипотезу о нормальном законе распределения генеральной совокупности.
Дата: 2019-02-19, просмотров: 235.
