Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Лекция № 1

Тема : Алгебра событий

План:

1. События, их классификация, вероятность события.

2. Операции над событиями.

3. Непосредственные вычисления вероятности (классический, геометрический, статистический метод).

4. Теорема сложения и умножения вероятностей.

5. Формула Бернулли. Формулы полной вероятностей и Байеса.

6. Локальная и интегральная теорема Лапласа.

1. События, их классификация, вероятность события.

       Событием называется всякий факт, который может произойти или не произойти в результате опыта.

       При этом тот или иной результат опыта может быть получен с различной степенью возможности. Т.е. в некоторых случаях можно сказать, что одно событие произойдет практически наверняка, другое практически никогда.

       В отношении друг друга события также имеют особенности, т.е. в одном случае событие А может произойти совместно с событием В, в другом – нет.

       События называются несовместными, если появление одного из них исключает появление других.

       Классическим примером несовместных событий является результат подбрасывания монеты – выпадение лицевой стороны монеты исключает выпадение обратной стороны (в одном и том же опыте).

       Полной группой событий называется совокупность всех возможных результатов опыта.

       Достоверным событием называется событие, которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта.

       Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий.

       События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.

       В приведенном выше примере появление красного и зеленого шаров – равновозможные события, если в коробке находится одинаковое количество красных и зеленых шаров.

       Если же в коробке красных шаров больше, чем зеленых, то появление зеленого шара – событие менее вероятное, чем появление красного.

Исходя из этих общих понятий можно дать определение вероятности.    Вероятностью события называется число, являющееся выражением меры объективной возможности появления события.

       Очевидно, что вероятность достоверного события равна единице, а вероятность невозможного – равна нулю. Таким образом, значение вероятности любого события – есть положительное число, заключенное между нулем и единицей .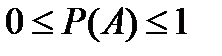

 

Операции над событиями.

       События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот.

 

       Объединением или суммой событий А _k называется событие A, которое означает появление хотя бы одного из событий А _k.

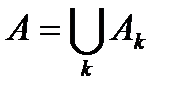
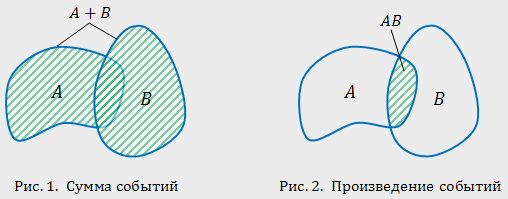
       Пересечением или произведением событий A_k называется событие А, которое заключается в осуществлении всех событий A_k.

 

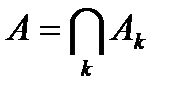
       Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В.

 

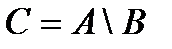
       Дополнительным к событию А называется событие 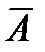, означающее, что событие А не происходит.

       Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают друг друга и в результате опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие.

       Совокупность всех элементарных исходов опыта называется пространством элементарных событий.

 

3. Непосредственные вычисления вероятности (классический, геометрический, статистический метод).

Классический метод определения вероятности.

Лекция № 2

Тема: Характеристики случайных величин. Распределения случайных величин

План:

1. Дискретные и непрерывные случайные величины.

2. Основные законы распределения дискретных и непрерывных случайных величин (биномиальный, геометрический, нормальный, показательный, равномерное распределение).

 

Лекция № 3

Тема: Распределения случайных величин

План:

1. Функция, плотность распределения.

2. Числовые характеристики (математическое ожидание, дисперсия, среднее квадратическое отклонение, мода, медиана).

 

Свойства дисперсии.

1) Дисперсия постоянной величины равна нулю: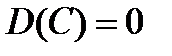

       2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: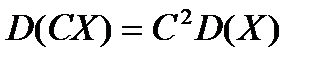

       3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: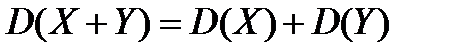

       4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин: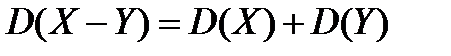

       Справедливость этого равенства вытекает из свойства 2.

 

       Теорема. Дисперсия числа появления события А в п независимых испытаний, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в каждом испытании.

 

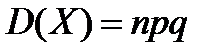
Лекция № 4

Тема: Формы представления статистических данных.

План:

1. Выборка из генеральной совокупности.

2. Статистический ряд.

 

Таблица 1.

          .

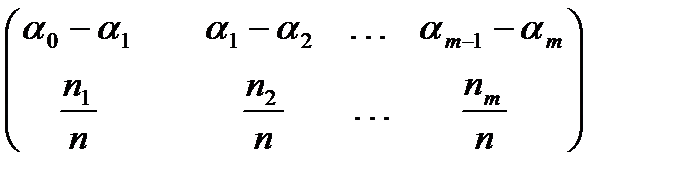       Элементы второй строки называются относительными частотами попадания в  интервал. Эта таблица называется выборочным распределением случайной величины .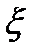

Очевидно, .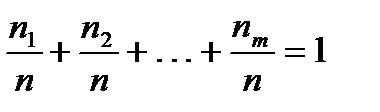

4) изобразим выборочное распределение на графике

f ^* ( x )

 

 

                              . .   .

 

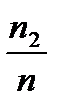
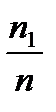
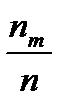
0

х                                                                                                                                                                             

.      .   .                                                      

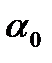
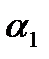
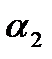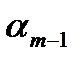
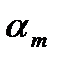
рис. 2

За единицу масштаба на оси абсцисс примем длину интервала 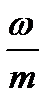. Очевидно, площадь построенной ступенчатой фигуры равна единице.

       Построенный график называется гистограммой относительных частот и представляет собой выборочный аналог плотности вероятности случайной величины.

 

Таблица 2.

       .

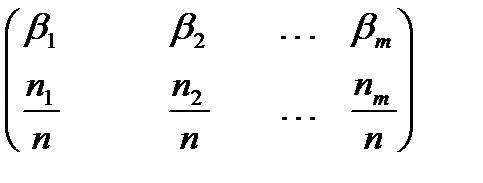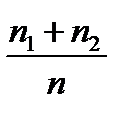
F*(x)

0

b1 b2 b3          × × ×          bm-1  bm

× × ×

x

1

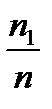
рис. 3

На оси ординат откладываем накопленные относительные частоты. Кружочки на графике означают, что соответствующие точки выброшены.

       Можно доказать, что при достаточно большом объеме выборки и при достаточно мелком делении интервалов с практической достоверностью 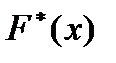 близка к истинной функции распределения F (x).

 

Лекция № 5

Тема: Оценка параметров распределения.

План:

1. Выборочные оценки параметров случайной величины. Основные требования к оценкам.

2. Состоятельные несмещенные оценки для математического ожидания, дисперсии, ковариации.

 

 

1. Выборочные оценки параметров случайной величины. Основные требования к оценкам

На практике эти параметры находятся приближенно по данным опыта.

       Пусть с испытанием связана случайная величина 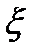 с неизвестным параметром 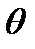, и пусть в результате серии независимых испытаний получена выборка 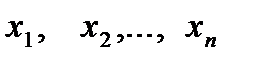. В качестве приближенного значения параметра  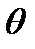принимают надлежащим образом выбранную комбинацию элементов выборки .

.

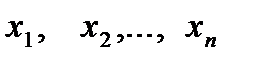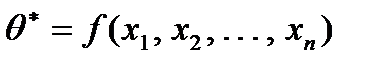Величина 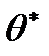 называется выборочной оценкой параметра .

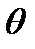К выборочным оценкам предъявляются следующие три основных требования: состоятельность, несмещенность, эффективность.

Чтобы были понятны даваемые далее определения этих понятий, обратим внимание на следующее: до выполнения испытаний числа 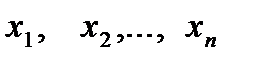 представляют собой независимые случайные величины, подчиненные одному и тому же закону распределения, совпадающему с законом распределения случайной величины 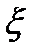, поэтому  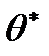также является случайной величиной, и имеет смысл говорить о математическом ожидании, дисперсии, СКО и т.д. случайной величины .

 

 

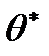Доказательство

 1. Мы знаем, что элементы выборки 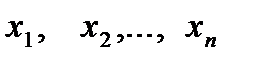 являются независимыми случайными величинами с одним и тем же законом распределения, совпадающим с законом распределения случайной величины 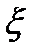, а значит, имеют те же числовые характеристики (а, D).

       По теореме Чебышева среднее арифметическое независимых случайных величин с одинаковыми параметрами (а, D), при неограниченном возрастании числа слагаемых сходится по вероятности к общему математическому ожиданию

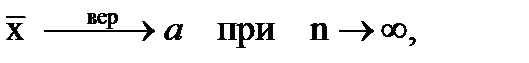
что и означает состоятельность оценки.

2. Имеем       

 

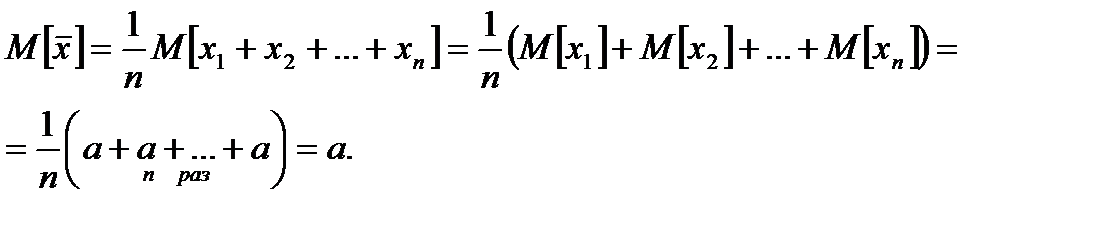
Это означает несмещенность оценки .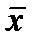

 

Лемма 2. Статистика

 

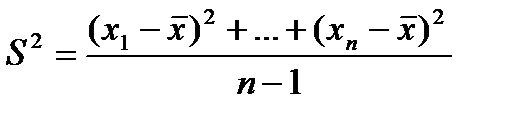
является состоятельной несмещенной оценкой дисперсии D. (Доказывается аналогично лемме 1).

Замечание 1. Если в формуле заменить (n - 1) на n , то оценка останется состоятельной, но будет смещенной. Величина S² называется исправленной дисперсией.

Замечание 2. Из леммы 2 следует, что статистика:

 

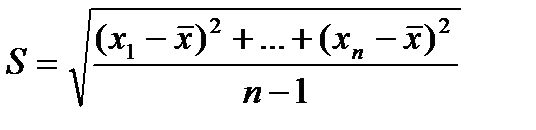
является состоятельной оценкой для СКО 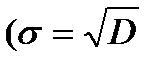). Можно доказать, что 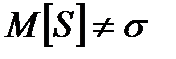, т.е. оценка S является смещенной оценкой для .

       Пусть по данным опыта получим ряд значений случайной точки ( 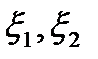) (выборка):

(х₁, у₁) (х₂, у₂), …, (х_n, у_n).

Справедлива следующая

Лемма 3. Состоятельной несмещенной оценкой для cov( 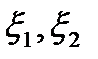) является выборочная ковариация

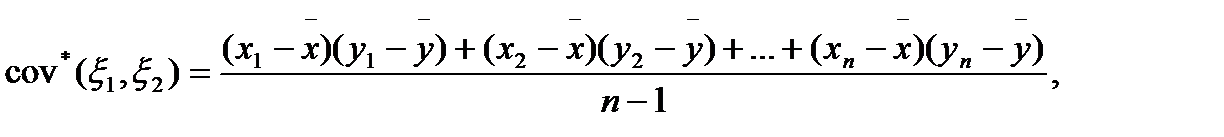
где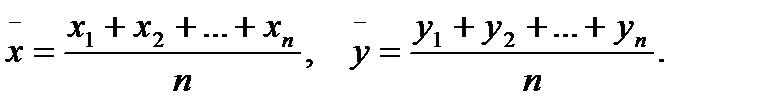

Рис. 3

Зададим число  pÎ (0, 1).

Квантилем уровня p распределения F ( x ) называется корень уравнения F(x) = p ,   х - ?

Обозначим его 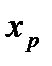 (см. рис. 3). Из определения функции F(x) вытекает: .

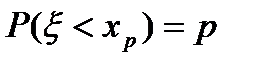Нам понадобится далее квантили распределений Пирсона и Стьюдента. Они обозначаются: ,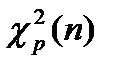

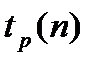
       Для этих квантилей имеются таблицы.

 

Лекция № 6

Тема: Проверка статистических гипотез

План:

1. Основные определения (статистическая гипотеза и примеры, классификация, ошибки 1-го и 2-го рода). Критерии согласия.

2. Параметрические гипотезы.

 

       Статистикой будем называть любую функцию 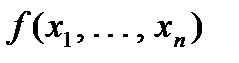 от выборки .

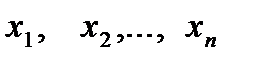Статистической называется гипотеза о предполагаемом виде неизвестного распределения или утверждение относительно значений одного или нескольких параметров известного распределения.

       Примеры статистических гипотез: генеральная совокупность наблюдаемых значений распределена по закону Пуассона, дисперсия двух нормальных совокупностей, равных между собой.

По содержанию статистические гипотезы можно классифицировать:

       1. Гипотезы о типе вероятностного закона распределения случайной величины, характеризующего явление или процесс.

       2. Гипотезы об однородности двух или более обрабатываемых выборок. Изучаемое свойство исследуется с помощью двух или более генеральных совокупностей. Гипотеза в этом случае может заключаться в следующем: исследуемые выборочные характеристики различаются между собой статистически значимо или нет.

       3. Гипотезы о свойствах числовых значений параметров исследуемой генеральной совокупности. Больше ли значения параметров некоторого заданного номинала или меньше и т.д.

       4. Гипотезы о вероятностной зависимости двух или более признаков, характеризующих различные свойства рассматриваемого явления или процесса. При этом определяется характер этой зависимости.

Наряду с выдвинутой гипотезой рассматривают и противоположную ей. Если выдвинутая гипотеза будет отвергнута, то имеет место противоположная ей. По этой причине гипотезы делят на:

1. нулевые (основная);

2. конкурирующие (альтернативной).

 

       Гипотеза, которая подвергается проверке, называется нулевой и обозначается H₀. Альтернативной гипотезой H₁ (от Hypothesis – «гипотеза» (англ.)) называется гипотеза, конкурирующая с нулевой, т. е. ей противоречащая. Простой называется гипотеза, содержащая только одно предположение.

Кроме того гипотезы делят на простые и сложные. Простой называют гипотезу, содержащую только одно предположение.

Сложной называют гипотезу, состоящую из конечного или бесконечного числа простых гипотез.несколько простых гипотез. Например гипотеза Н: 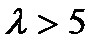 содержит бесчисленное множество простых гипотез Н_i: 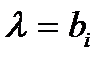,где 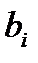-любое число большее 5.

Пример. Пусть проверяется гипотеза о равенстве некоторого параметра a значению a₀ , т. е. гипотеза H₀: a = a₀. В этом случае альтернативной гипотезой можно рассматривать одну из следующих гипотез:H₁: a > a₀; H₁: a < a₀; H₁: a ≠ a₀; H₁: a > 2. Все приведенные гипотезы простые, и только H₁: a > 2– сложная гипотеза.

 

Выбор альтернативной гипотезы определяется формулировкой решаемой задачи. Причина выделения нулевой гипотезы состоит в том, что чаще всего такие гипотезы рассматриваются как утверждения, которые более ценны, если они опровергаются. Это основано на общем принципе, в соответствии с которым теория должна быть отвергнута, если есть противоречащий ей факт, но не обязательно должна быть принята, если противоречащих ей фактов на текущий момент нет.

Правило, по которому выносится решение принять или отклонить гипотезу H₀, называется статистическим критерием. Проверка статистических гипотез осуществляется по результатам наблюдений (экспериментов, опытов), из которых формируют функцию результатов наблюдений, называемую проверочной статистикой. Таким образом, статистический критерий устанавливает, при каких значениях этой статистики проверяемая гипотеза принимается, а при каких она отвергается.

Правило проверки гипотезы о законе распределения:

1. Задаются уровнем значимости 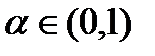 и вычисляют квантиль .

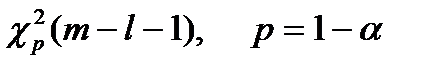2. Выполняют выборку 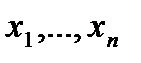 и по формуле вычисляют .

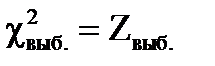3. Если 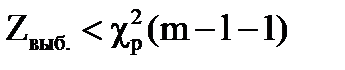, гипотеза принимается.

Если 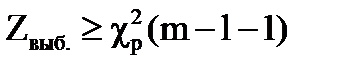, гипотеза отвергается.

 

При проверке гипотез по указанному правилу возможны ошибки двух типов:

1. Ошибка первого рода: отвергается верная гипотеза. Вероятность этой ошибки равна уровню значимости a. Действительно, из определения a имеем:

Р (ошибки 1-го рода)=

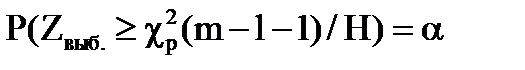
2. Ошибка второго рода: принимается неверная гипотеза. Вероятность этой ошибки обозначают b:

Р (ошибки второго рода)=  .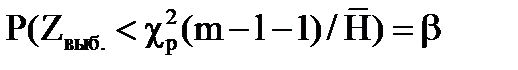

В конкретной ситуации эта вероятность может быть вычислена.

В математической статистике доказывается: при фиксированном объеме выборки уменьшение уровня значимости a влечет увеличение b и обратно, уменьшение b влечет увеличение a.

       Единственный способ уменьшения одновременно a и b - это увеличение объема выборки.

       В конкретных ситуациях можно минимизировать вероятность той ошибки, которая ведет к менее тяжелым последствиям. Рекомендуется, если это возможно, проводить проверку более одного раза (набрать хотя бы еще одну выборку).

       Мощностью критерия называется вероятность отвергнуть неверную гипотезу:

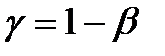, где b - вероятность ошибки второго рода.

Малое значение вероятности α, используемое при проверке гипотезы, называется уровнем значимости критерия. Интервал значений 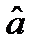, для которых гипотезу следует отвергнуть, называется областью отклонения гипотезы, или критической областью. Интервал значений 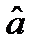, при которых гипотезу следует принять, носит название области принятия гипотезы (см. рис. 1).

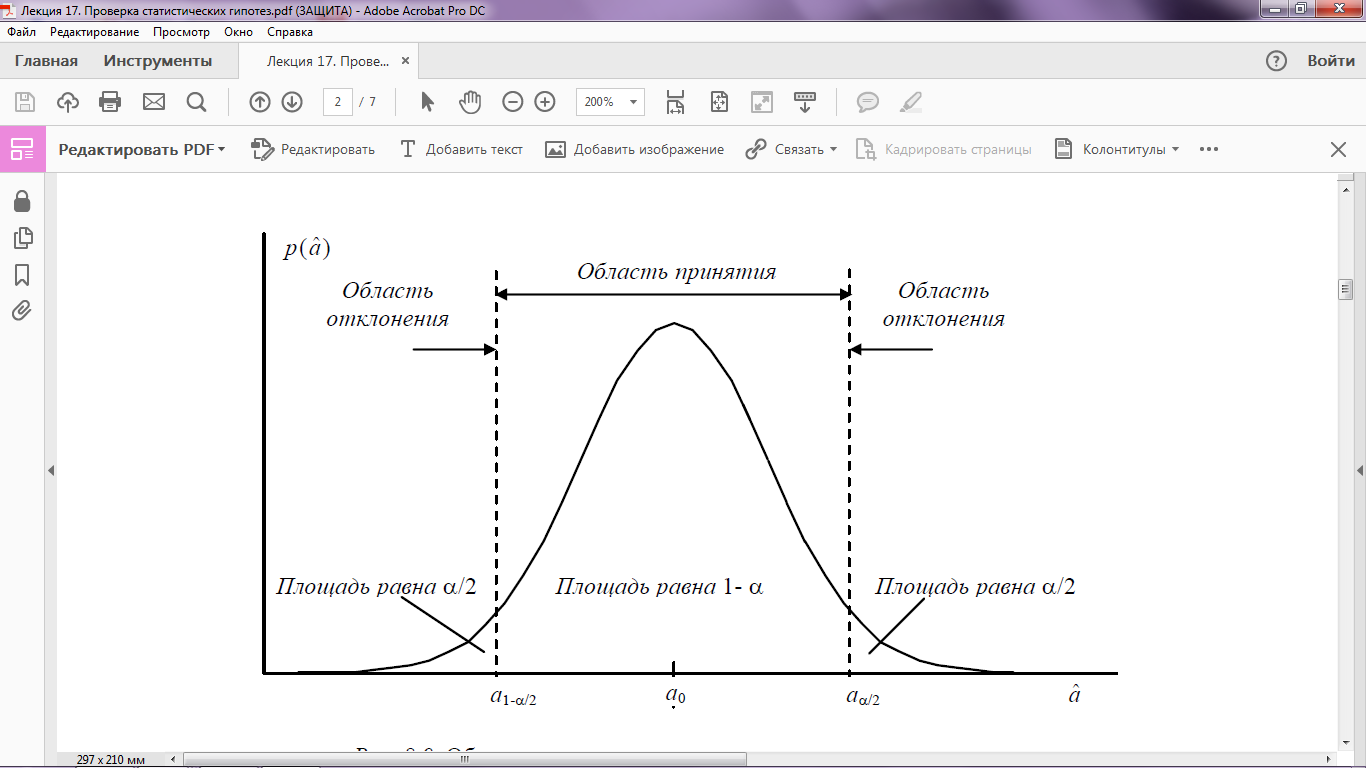
Рис.1. Области принятия и оклонения при проверке гипотез

 

Приведенный способ проверки гипотезы называется двусторонним критерием, так как если гипотеза H₀ верна, то величина 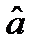 может быть как больше, так и меньше a₀. Необходимо проверять значимость расхождения между  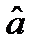и a₀ с обеих сторон. В некоторых задачах может оказаться достаточно одностороннего критерия.

Например, пусть гипотеза состоит том, что a ≥ a₀. В этом случае гипотеза будет ошибочной только тогда, когда a < a₀, а критерий будет использовать только нижнюю границу плотности распределения p( ).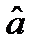

Как видно на рис. 1, ошибка первого рода происходит в том случае, когда при справедливости гипотезы 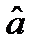 попадает в область ее отклонения. Таким образом, вероятность ошибки первого рода равна α, т. е. уровню значимости критерия.

Для того чтобы найти вероятность ошибки второго рода, следует определить каким-тообразом величину отклонения истинного значения параметра a от гипотетического значения параметра a₀, которое требуется определить. Предполагается, что истинное значение параметра a₀ в действительности равно a₀ + d или a₀ − d (см. рис. 2).

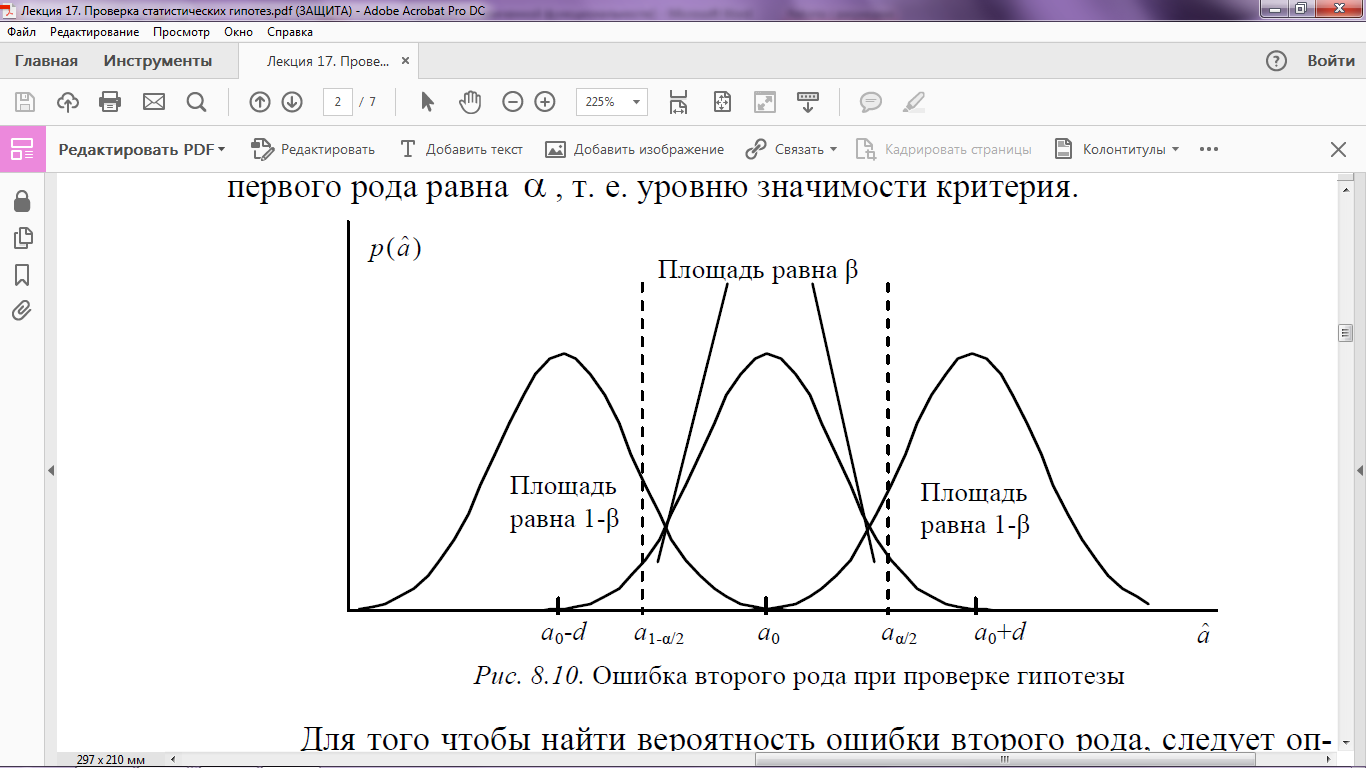
Рис.2. Ошибка второго рода при проверке гипотезы.

 

Если согласно гипотезе H₀: a = a₀, а на самом деле a = a₀ ± d, то вероятность того, что 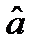 попадет в область принятия гипотезы H₀, т.е. в интервал (a_{1−α 2}, a_{α 2}), составляет β. Таким образом, вероятность ошибки второго рода равна β при выявлении отклонения истинного значения параметра a на ± d от гипотетической величины a₀.

 

       Под статистическим критерием называется случайная величина К с известным законом распределения, служащая для проверки нулевой гипотезы.

Различают три вида критериев:

       1) Параметрические критерии - критерии значимости, которые служат для проверки гипотез о параметрах распределения генеральной совокупности при известном виде распределения.

       2) Критерии согласия - позволяют проверить гипотезы о соответствии распределений генеральной совокупности известной теоретической модели.

       3) Непараметрические критерии - используются в гипотезах, когда не требуется знаний о конкретном виде распределения.

 

       Задача проверки статистических гипотез сводится к исследованию генеральной совокупности по выборке. Множество возможных значений элементов выборки может быть разделено на два непересекающихся подмножества- критическую область и область принятия гипотезы.

       Наблюдаемые значения критерия (статистика) K_набл называют такое значение критерия, которое находится по данным выборки.

       Границы критической области, отделяющие ее от области принятия гипотезы, называют критическими точками и обозначают K_кр.

       Критической областью называют область значений критерия, при которых нулевую гипотезу отвергают, областью принятия гипотезы – область значений критерия, при которых гипотезу принимают. Итак, процесс проверки гипотезы состоит из следующих этапов:

· выбирается статистический критерий К;

· вычисляется его наблюдаемое значение К_набл по имеющейся выборке;

· поскольку закон распределения К известен, определяется (по известному уровню значимости α) критическое значение k_кр, разделяющее критическую область и область принятия гипотезы (например, если р(К > k_кр) = α, то справа от kкр располагается критическая область, а слева – область принятия гипотезы);

· если вычисленное значение Кнабл попадает в область принятия гипотезы, то нулевая гипотеза принимается, если в критическую область – нулевая гипотеза отвергается.

Различают разные виды критических областей:

· правостороннюю критическую область, определяемую неравенством K > k_кр (k_кр > 0);

· левостороннюю критическую область, определяемую неравенством K < k_кр ( k_кр < 0);

· двустороннюю критическую область, определяемую неравенствами K < k₁, K > k₂ (k₂ > k₁).

Критерии согласия

       Критериями согласия называют критерии, в которых гипотеза определяет закон распределения либо полностью, либо с точностью до небольшого числа параметров. Существует несколько различных критериев согласия: критерий Смирнова, критерий Колмогорова, критерий χ²- Пирсона и др.

 

       Рассмотрим универсальный критерий согласия Пирсона. Проверка гипотезы о том, что эмпирическая частота мало отличается от соответствующей теоретической частоты, осуществляется с помощью величины χ²- меры расхождения между ними.

       Любая аналитическая функция f(x), с помощью которой аппроксимируется статистическое распределение, должна обладать основными свойствами плотности распределения:

f (x) ≥ 0

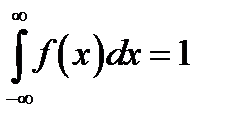
Чтобы оценить, насколько хорошо выбранный теоретический закон распределения согласуется с экспериментальными данными, используются так называемые критерии согласия. Таких критериев существует несколько, но наиболее часто применяется критерий согласия χ², предложенный Пирсоном. Является непараметрическим критерием проверки статистических гипотез.

Пусть проведено n независимых опытов, в каждом из которых случайная величина X приняла определенное значение. Результаты опытов сведены в k интервалов, и построены статистический ряд, выборочная функция распределения и гистограмма, т.е. экспериментальные данные описываются выборочным законом распределения P*(x). Необходимо проверить, согласуются ли экспериментальные данные с гипотезой H₀: P(x) = P*(x) о том, что случайная величина X имеет выбранный теоретический закон распределения P(x), который может быть задан функцией распределения F(x) или плотностью f(x). Альтернативная гипотеза в этом случае – H₁: P(x) ≠ P*(x).

Знание теоретического закона распределения позволяет найти теоретические вероятности попадания случайной величины в каждый интервал

(x_i, x_{i+ 1}), i = 1, k: p₁, p₂, K, p_k.

Проверка согласованности теоретического и статистического распределений сводится к оценке расхождений между теоретическими вероятностями p_i и полученными частотами p^*_i. В качестве меры расхождения удобно выбрать сумму квадратов отклонений(p^*_i  − p_i), взятых с некоторыми «весами» c_i:

 

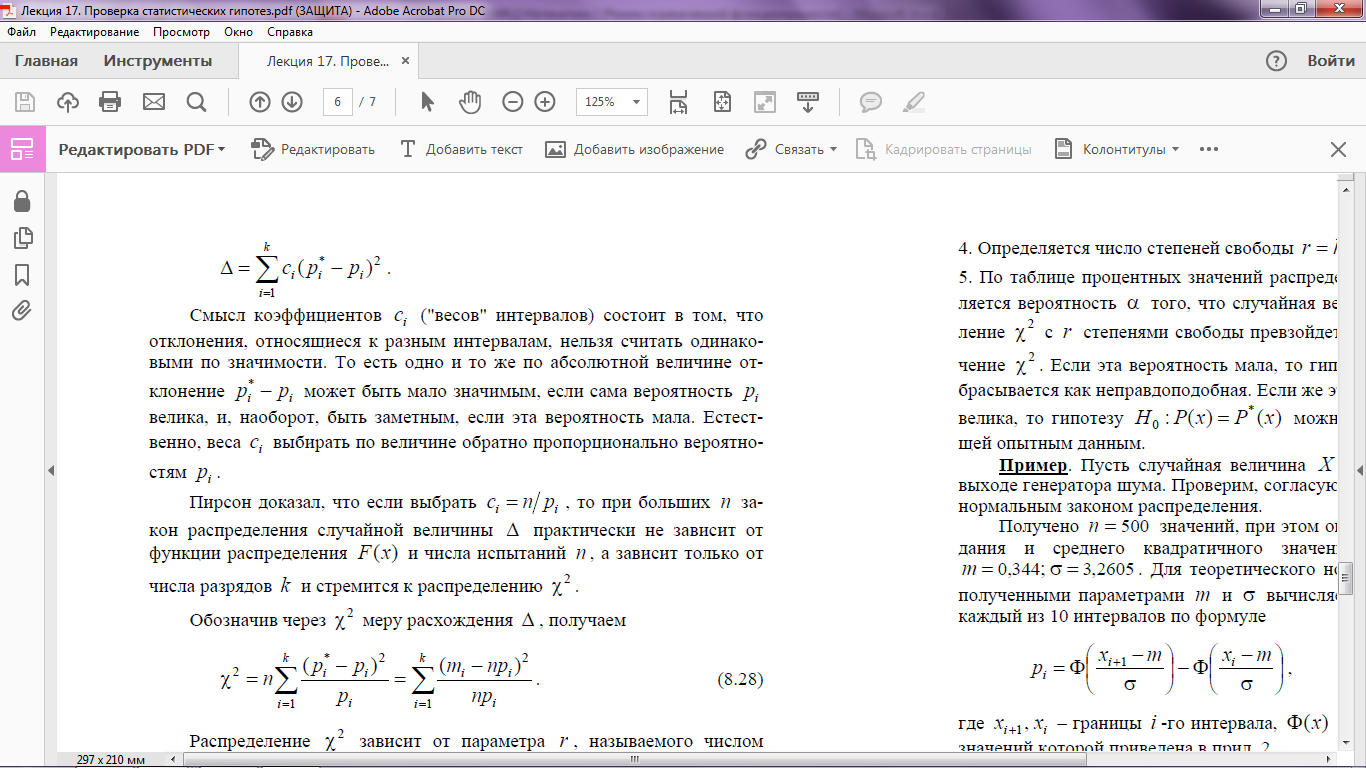
Смысл коэффициентов c_i («весов» интервалов) состоит в том, что отклонения, относящиеся к разным интервалам, нельзя считать одинаковыми по значимости. То есть одно и то же по абсолютной величине отклонение p^*_i  − p_i может быть мало значимым, если сама вероятность p_i велика, и, наоборот, быть заметным, если эта вероятность мала. Естественно, веса c_i выбирать по величине обратно пропорционально вероятностям p_i. Пирсон доказал, что если выбрать c_i = n/p_i, то при больших n закон распределения случайной величины практически не зависит от функции распределения F(x) и числа испытанийn, а зависит только от числа разрядов k и стремится к распределению χ². Обозначив через χ² меру расхождения , получаем:

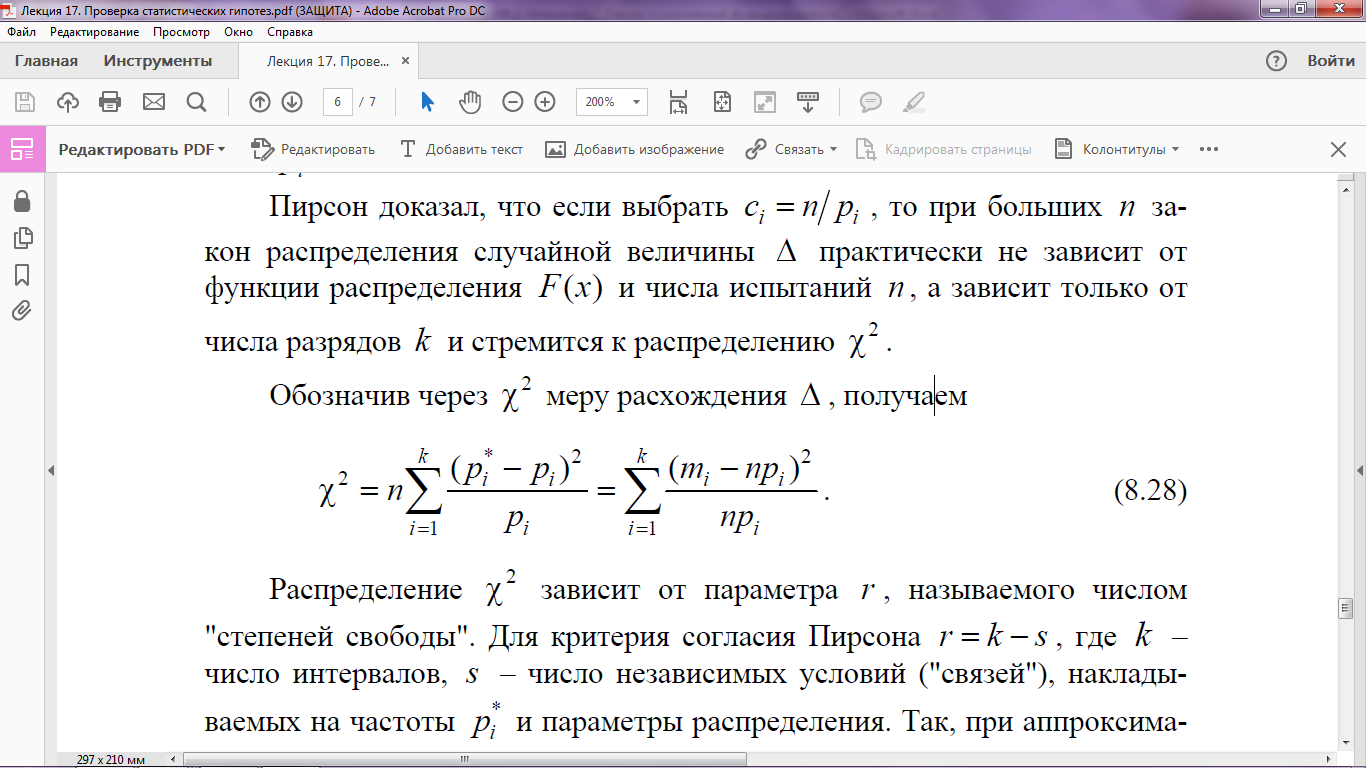
       Распределение зависит от параметра r, называемого числом степеней свободы, которое равно:

r = k − s,

где k – число интервалов, s – число независимых условий («связей»), накладываемых на частоты p* и параметры распределения. Так, при аппроксимации нормального распределения s = 3, а при исследовании распределения Пуассона s = 2.

       Схема применения критерия χ² для оценки согласованности теоретического и статистического распределения сводится к следующим процедурам (этапам):

       1. На основании полученных экспериментальных данных x₁, x₂, K, xnрассчитываются значения частот p^*_i в каждом из k интервалов.

       2. Вычисляются, исходя из теоретического распределения, вероятности p_i попадания значений случайной величины в интервалы(x_i, x_i + 1).

       3. По формуле   рассчитывается значение χ².

       4. Определяется число степеней свободы r = k − s.

       5. По таблице процентных значений распределения χ² определяется вероятность α того, что случайная величина, имеющая распределение χ² с r степенями свободы превзойдет полученное на этапе 3 значение χ². Если эта вероятность мала, то гипотеза H₀: P(x) = P*(x) отбрасывается как неправдоподобная. Если же эта вероятность относительно велика, то гипотезу H₀: P(x) = P*(x) можно признать не противоречащей опытным данным.

Пример. Пусть случайная величина X – значения напряжения на выходе генератора шума. Проверим, согласуются ли полученные данные с нормальным законом распределения.

Получено n = 500 значений, при этом оценки математического ожидания и среднего квадратичного значения соответственно равны: m = 0,344; σ = 3,2605. Для теоретического нормального распределения с полученными параметрами m и σ вычисляем вероятности попадания в каждый из 10 интервалов по формуле

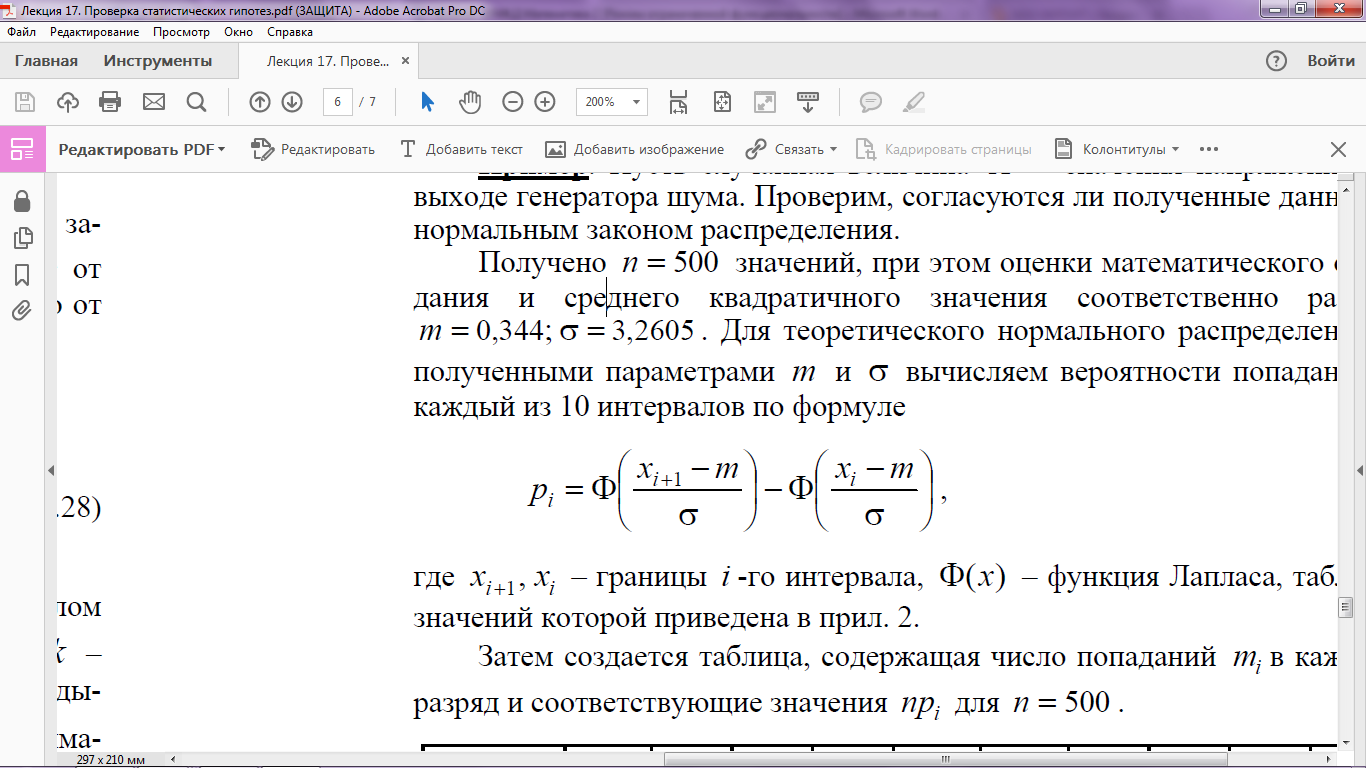
x_{i + 1}, x_i – границы i -гоинтервала,Φ(x) – функция Лапласа (табличная).

Затем создается таблица, содержащая число попаданий m i в каждый разряд и соответствующие значения npi для n = 500.

 

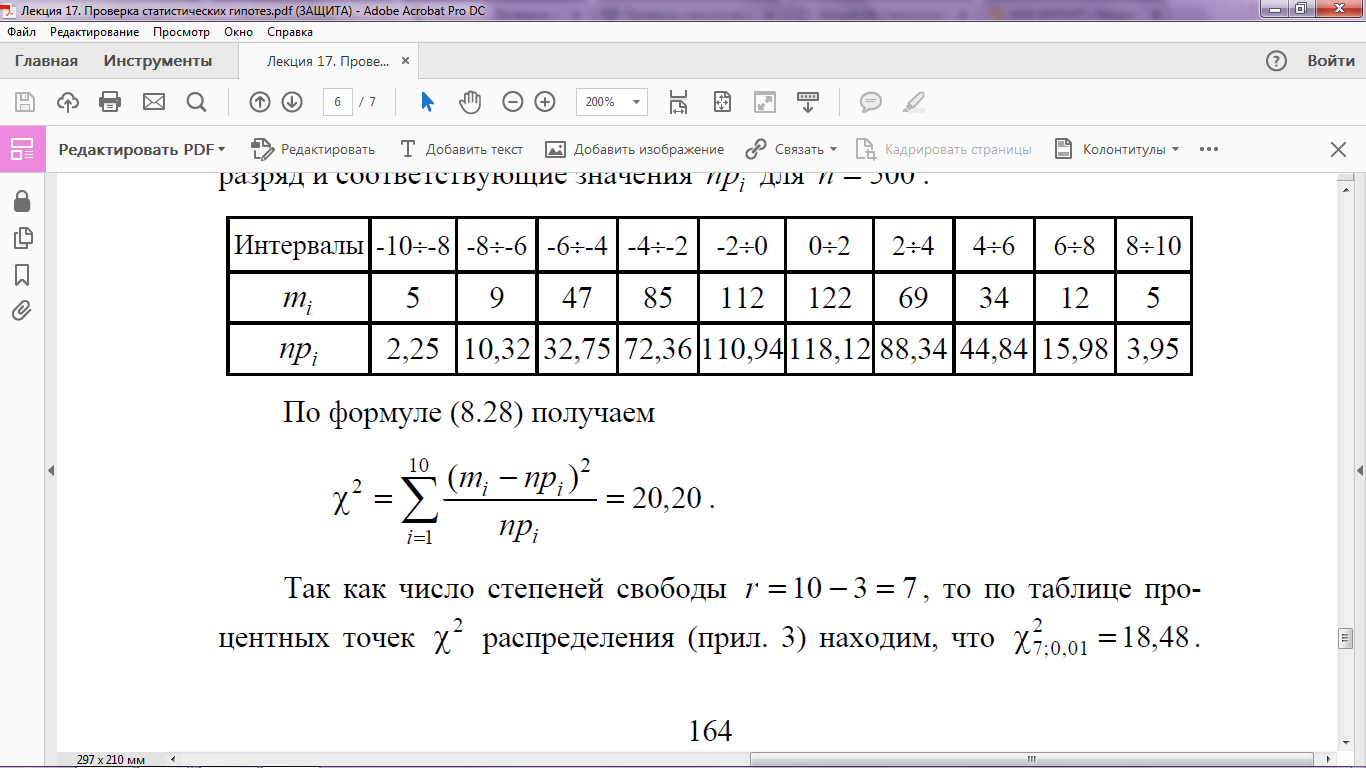
По формуле для χ²:

 

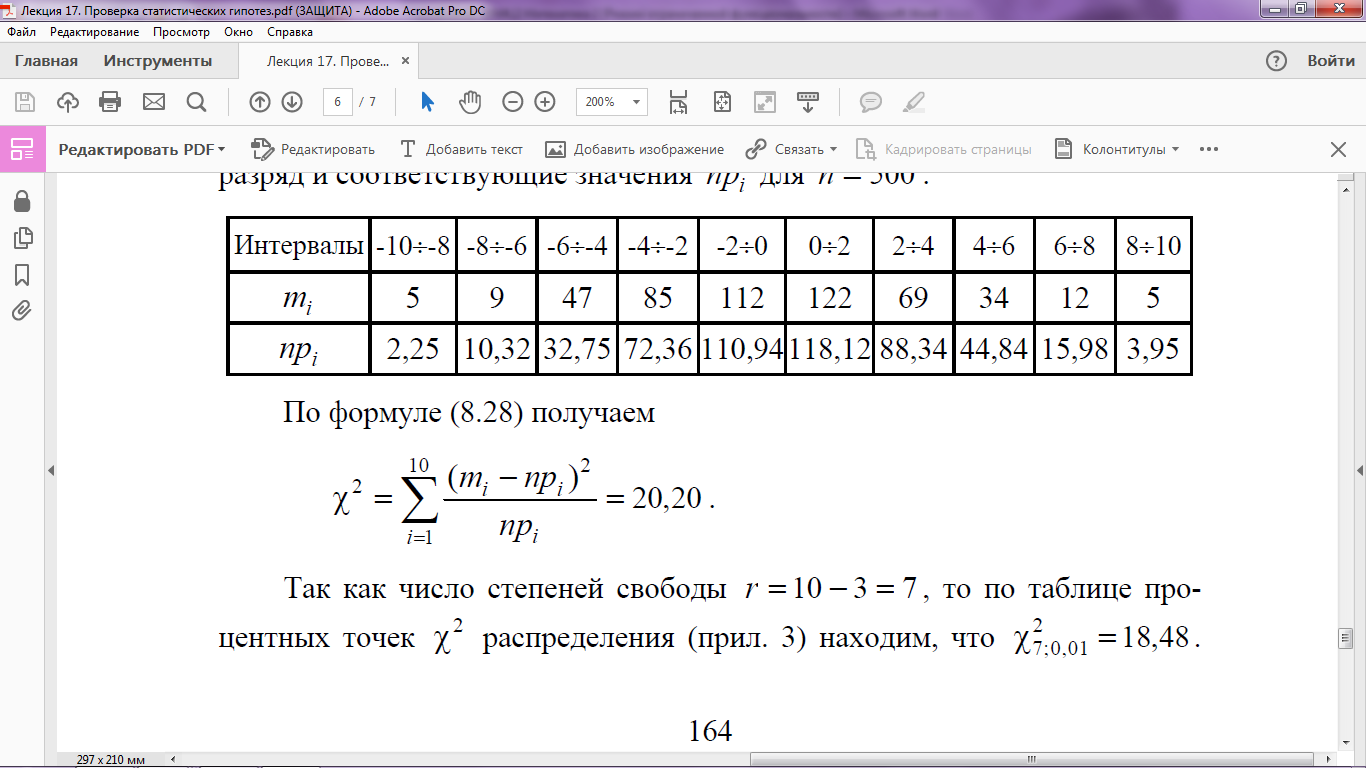
Так как число степеней свободы r = 10 − 3 = 7, то по таблице процентных точек χ² распределения находим, что χ²_{7; 0,01} = 18,48

       Поскольку χ² > χ²_7;0,01 для малой вероятности α = 0,01, следует признать: полученные экспериментальные данные противоречат проверяемой гипотезе о том, что случайная величина X распределена по нормальному закону.

       При использовании критерия согласия (χ² или любого другого) положительный ответ нельзя рассматривать как утвердительный о правильности выбранной гипотезы. Определенным является лишь отрицательный ответ, т.е. если полученная вероятность α мала, то можно отвергнуть выбранную гипотезу H₀: P(x) = P*(x) и отбросить ее как явно не согласующуюся с экспериментальными данными. Если же вероятность α велика, то это не может считаться доказательством справедливости гипотезы

H₀: P(x) = P*(x), а указывает только на то, что гипотеза не противоречит экспериментальным данным.

При использовании критерия согласия χ² достаточно большими должны быть не только общее число опытов n (несколько сотен), но и значения m_i в отдельных интервалах. Для всех интервалов должно выполняться условие m_i ≥ 5. Если для некоторых интервалов это условие нарушается, то соседние интервалы объединяются в один.

 

Схема применения критерия

       1. Выдвижение начальной гипотезы 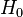, состоящей в том, что случайная величина X распределена по нормальному закону распределения.

       2. Необходимо сравнить эмпирические (найденные экспериментальным путем) и теоретические (найденные исходя из закона распределения) частот. Однако как бы точно не был подобран закон распределения между теоретическими и эмпирическими частотами неизбежны расхождения возникает вопрос, объяснимы ли эти расхождения только случайными факторами, связанные с ограниченным числом наблюдений, или это связано с неправильным выбором теоретического закона распределения. Критерий Пирсона позволяет ответить на этот вопрос, однако как и любой другой критерий, он не доказывает справедливости гипотез, а лишь устанавливает ее согласие или несогласие с экспериментальными данными на принятом уровне значимости. В качестве проверки нулевой гипотезы применяется случайная величина χ², которая вычисляется по формул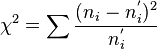е  где 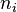 - эмпирические частоты,  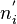- теоретические частоты.

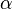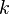       3. По таблице χ²-Пирсона находят критические значения χ², которое зависит от двух параметров  и , где 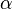 - заданный уровень значимости (обычно 0,05 0,01 0,1) (то есть с вероятностью 0,95 0,99 0,9 можно гарантировать принятие или опровержение гипотезы)  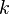- число степеней свободы. Оно находится по формул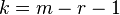е , где 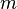 - число групп (интервалов в вариационном ряду),  - число параметров распределения (для нормального распределения 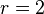, для показательного распределения 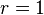, для равномерного )

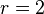       4. Необходимо сравнить χ² критическое и χ² наблюдаемое. Если χ² критическое больше χ² наблюдаемого, то гипотеза принимается, если χ² критическое меньше χ² наблюдаемого, то гипотеза опровергается.

       5. Сделать вывод из пункта 1.

Параметрические гипотезы.

       В тех случаях, когда известен закон, но неизвестны значения его параметров (дисперсия или математическое ожидание) в конкретной ситуации, статистическую гипотезу называют параметрической.

       Например, предположение об ожидаемом среднем доходе по акциям или разбросе дохода являются параметрическими гипотезами.

       Большинство параметрических методов разработаны для нормально распределенных совокупностей. Некоторые методы позволяют анализировать данные, распределенные по другим законам (например, биномиальному или Пуассона).

       Когда закон распределения генеральной совокупности не известен, но есть основания предположить, каков его конкретный вид, выдвигаемые гипотезы о виде его распределения называются непараметрическими.

       Например, можно выдвинуть гипотезу, что число дневных продаж в магазине или доход населения подчинены нормальному закону распределения.

       Непараметрические методы позволяют исследовать данные без допущений о характере распределения переменных. Так как в этих тестах обрабатывается не само измеренное значение, а его ранг, то эти тесты нечувствительны к выбросам. Непараметрические тесты могут применяться в тех случаях, когда переменные измерены при помощи порядковой или метрической шкалы. Существуют тесты, предназначенные для анализа номинальных данных.

       Непараметрические методы наиболее приемлемы, когда объем выборок мал. Если данных много (например, n > 100), то не имеет смысла использовать непараметрические статистики. Когда выборки становятся очень большими, то выборочные средние подчиняются нормальному закону, даже если исходная переменная не является нормальной или измерена с погрешностью.

        Таким образом, параметрические методы, являющиеся более чувствительными (имеют большую статистическую мощность), практически всегда подходят для больших выборок.

       Предположение, которое касается неизвестного значения параметра распределения, входящего в некоторое параметрическое семейство распределений, называется параметрической гипотезой (напомним, что параметр может быть и многомерным). Предположение, при котором вид распределения неизвестен (т.е. не предполагается, что оно входит в некоторое параметрическое семейство распределений), называется непараметрической гипотезой. Таким образом, если распределение F(x) результатов наблюдений в выборке согласно принятой вероятностной модели входит в некоторое параметрическое семейство {F(x; θ), θ 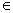Θ}, т.е. F(x) = F(x;θ₀) при некотором θ₀ 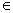Θ, то рассматриваемая гипотеза – параметрическая, в противном случае – непараметрическая.

       Если и H₀ и H₁ – параметрические гипотезы, то задача проверки статистической гипотезы – параметрическая. Если хотя бы одна из гипотез H₀ и H₁ – непараметрическая, то задача проверки статистической гипотезы – непараметрическая. Другими словами, если вероятностная модель ситуации – параметрическая, т.е. полностью описывается в терминах того или иного параметрического семейства распределений вероятностей, то и задача проверки статистической гипотезы – параметрическая.

 

Традиционный метод проверки однородности двух независимых выборок (критерий Стьюдента)

       Наиболее распространенный метод проверки однородности выборок путем выдвижения и проверки параметрических гипотез основан на применении критерия Стьюдента.

       Рассмотрим случай сравнения двух независимых выборок.

       Выдвигаются: нулевая гипотеза о равенстве средних и альтернативная, о том, что средние не равны.

       Вычисляют выборочные средние арифметические и дисперсии в каждой выборке и статистику Стьюдента t, на основе которой принимают решение.

       По заданному уровню значимости a и числу степеней свободы (m + n - 2) из таблиц распределения Стьюдента находят критическое значение t_кр. Если |t| > t_кр, то гипотезу однородности (отсутствия различия) отклоняют, если же |t| < t_кр, то принимают.

Общая постановка задачи проверки гипотез:

       1. Формулируют (выдвигают) нулевую гипотезу H₀ об отсутствии различий между группами, об отсутствии существенного отличия фактического распределения от некоторого заданного, например, нормального, экспоненциального и др.

Сущность нулевой гипотезы H₀: разница между сравниваемыми генеральными параметрами равна нулю, и различия, наблюдаемые между выборочными характеристиками, носят случайный характер, то есть эти выборки принадлежат одной генеральной совокупности.

       2. Формулируют противоположную нулевой, альтернативную гипотезу H₁.

       3. Задают уровень значимости α. Уровень значимости α – это вероятность ошибки отвергнуть нулевую гипотезу H₀, если на самом деле эта гипотеза верна. При α ≤ 0,05 ошибка возможна в 5% случаев.

       4. Для проверки выдвинутой гипотезы используют критерии.

       Критерий – это случайная величина К. которая служит для проверки H₀. Эти функции распределения известны и табулированы. Критерий зависит от двух параметров: от числа степеней свободы и от уровня значимости α. Фактическую величину критерия получают по данным наблюдения К_набл.

       5. По таблице определяют критическое значение, превышение которого при справедливости гипотезы маловероятно К_крит(α, f).

       6. Сравнивают Кнабл и К_крит(α, f).

Если К_набл > К_крит(α, f), то отвергают H₀ и принимают H₁.

Если К_набл < К_крит(α, f) то принимают H₀.

Это для параметрических критериев.

Если использованы непараметрические критерии, то наоборот: если К_набл > К_крит(α, f), то принимают H₀.

       7. Вывод: различие статистически значимо (α ≤ 0,05) или незначимо.

 

       Параметрические критерии представляют собой функции параметров данной совокупности и используются, если совокупности. Из которых взяты выборки, подчиняются нормальному закону распределения.

       Непараметрические критерии применяются, если нет подчинения распределения нормальному закону. Эти критерии обычно заменяют данные выборки знаками (+ или -), рангами (т.е. числами 1; 2; 3;…, описывающими их положение в упорядоченном наборе данных), категориями и т.п. Непараметрический критерий можно использовать, если объем выборки небольшой настолько, что невозможно оценить закон распределения данных.

 

Лекция № 7

Тема: Математическая формулировка экономических и производственных задач

План:

1. Представление ограничений ресурсов, капиталовложений и т.д. в виде линейных неравенств.

2. Определение функции цели и нахождение вектора решений, удовлетворяющего задаче с заданными ограничениями.

 

Сырье

Нормы расхода сырья

Запас сырья

А В С Какао 18 15 12 360 Сахар 6 4 8 192 Наполнитель 5 3 3 180 Прибыль 90 100 160 максимум Объем выпуска Х1 Х2 Х3  

 

Экономико-математическая формулировка задачи имеет вид: Найти такие значения переменных Х = (х₁, х₂, х₃), чтобы целевая функция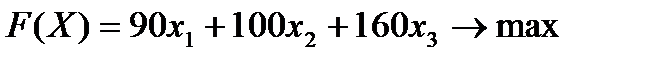

 при условиях-ограничениях:

 

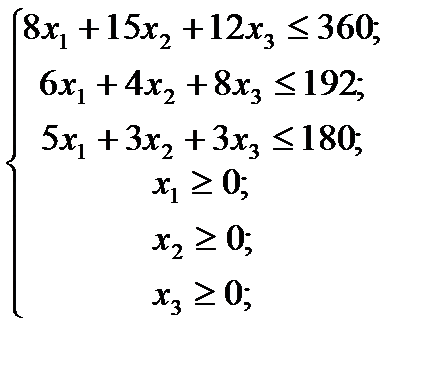
       Оптимизационная модель - экономико-математическая модель, которая охватывает некоторое число вариантов производства, распределения или потребления и предназначена для выбора таких значений переменных, характеризующих эти варианты, чтобы был найден лучший из них. Кроме системы ограничений включает критерий для выбора, особое уравнение, называемое целевой функцией. С помощью такого критерия находят решение, наилучшее по какому-либо показателю, напр. минимум затрат на материалы при заданном объеме продукции или, максимум прибыли при заданных ограничениях по ресурсам и т. д.

       Оптимизационная модель является основным инструментом экономико-математических методов. Оптимизационные модели разного характера часто сводятся к задачам линейного программирования.

   Среди линейных моделей математического программирования особое место занимают четыре типа моделей:

1) модель общей задачи линейного программирования;

2) модель транспортной задачи линейного программирования;

3) модель распределительной задачи линейного программирования;

4) модель ассортиментной задачи линейного программирования.

   Модель общей задачи линейного программирования применяют для решения задач планирования в торговле, использования сырья, определения оптимального плана выпуска изделий и др.

   В торговле планирование связано с поиском наиболее выгодного варианта распределения различного вида ресурсов: финансовых, трудовых, товарных, материальных, технических и др. Модель общей задачи линейного программирования применяют для решения широкого круга задач торговой практики, таких как планирование товарооборота; организация рациональных за­купок продуктов питания (задача о диете); замена торгового оборудования; определение ассортимента товаров для торговой базы в силу ограниченной площади хранения; установление рационального режима работы и т.д.

       Методика построения экономико-математической модели заключается в том, чтобы экономическую сущность задачи представить математически. Необходимо определить систему переменных величин. Рассчитать нужные технико-экономические коэффициенты и собрать соответствующие нормативные данные. Все условия задачи записать в виде уравнений или неравенств. Обосновать критерии оптимальности и выразить его математической формулой.

Как правило, выделяется шесть этапов:

· постановка экономической проблемы (задачи), ее качественный анализ и обоснование критерия оптимальности;

· формализация экономической проблемы и ее математическая запись;

· подготовка исходной информации и технико-экономических коэффициентов;

· построение математической модели;

· создание расчетной компьютерной модели и ее решение;

· анализ результатов решения и их практическое применение.

 

       В настоящее время множество задач планирования и управления в различных отраслях хозяйства решаются методами математического программирования (моделирования), наиболее развитым из которых в области оптимизационных задач является самый простой и доступный метод линейного программирования (МЛП). Этот метод позволяет описать широкий круг задач хозяйственной и коммерческой деятельности: планирование товароснабжения, распределение ресурсов, капиталовложений, организация рациональных перевозок товаров, распределение рабочей силы и специалистов и т.д.

       Если задача МП содержит только линейные функции, то ее называют задачей линейного программирования.

Лекция № 8

Тема: Графический способ определения оптимального плана

План:

1. Графическое решение задач с двумя неизвестными, заданных линейными неравенствами ограничений.

2. Построение выпуклого многоугольника возможных решений и определение оптимального плана с помощью градиента функции цели.

 

Лекция № 9

Тема: Симплексный метод для задач с естественным базисом

План:

Алгоритм симплекс-метода

1. Приводим систему ограничений к каноническому виду (когда система ограничена). Причём в системе можно выделить единичный базис.

2. Находим первоначальный опорный план (неотрицательные базисные решения системы уравнений КЗЛП). Каждый из опорных планов определяется системой m линейно независимых векторов, содержащихся в данной системе из n векторов А₁, А₂,…, А_n. Верхняя граница количества опорных планов, содержащихся в данной задаче, определяется числом сочетаний С_nm);

3. Строим симплексную таблицу (симплекс-таблица матрица, служащая средством перебора допустимых базисных решений (невырожденной) задачилинейного программирования при ее решении симплексным методом. Образуется из матрицы коэффициентов системы уравнений линейного программирования, приведенной к канонической форме, последовательное ее преобразование по так называемому симплексному алгоритму позволяет заограниченное количество шагов (итераций) получать искомый результат - план, обеспечивающий экстремальное значение целевой функции).

4. В симплексной таблице проверяем вектора на отрицательность, т.е. оценки Zj – С j записанные в 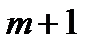строке должны быть ≤ 0 (на минимум), Zj – С j ≥ 0 (на максимум). Если оценки удовлетворяют условиям оптимальности то задача решена.

5. Если для некоторых векторов нарушаются условия оптимальности, то необходимо ввести в базис вектор, которому соответствует:

max [θ_{0 j} ( Zj – С j )] ;  min [θ_{0 j} ( Zj – С j )] ;   θ_{0 j} = min 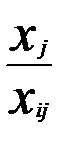 , где х _i > 0

       Элемент вектора θ _j который соответствует θ_{0 j}  называется разрешающим; строка и столбец в которых он находится, называется направляющим, из базиса уходит вектор, стоящий в направляющей строке.

6. Найдём коэффициент разложения для всех векторов в новом базисе. Применим метод Джордано Гаусса

Проверим на оптимальный опорный план. Если оценка удовлетворяет условиям оптимальности, то задача решена, если нет, то выполняются пункты 5-7.

 

2. Введение естественных базисных переменных. Построение симплексной таблицы. Определение нулевого плана.

Симплекс-метод наиболее эффективен при решении сложных задач и представляет итерационный (шаговый) процесс, начинающийся с нулевого (опорного) решения (вершины n-мерного многогранника). Далее в поисках оптимального варианта плана предполагается движение по угловым точкам (вершинам многогранника) до тех пор, пока значения целевой функции не достигнет максимальной (минимальной) величины. Рассмотрим алгоритм симплексного метода на примере задачи планирования товарооборота при ограниченных ресурсах сырья.

  Предприятие реализует n товарных групп, располагая m ограниченными материально-денежными ресурсами b_i ≥0 (1 ≤ i ≤ m) . Известны расходы ресурсов каждого i- вида на производство и реализацию единицы товара каждой группы, представленные в виде матрицы (a_ij) и прибыль, получаемая предприятием от реализации единицы товара j-группы, входящая в целевую функцию Z(X). Метод линейного программирования не отличается от системы (1) - (2):

                         Z(X) = с₁ Х₁ + с₂ Х₂ + с₃ Х₃ + … +с_n Х_n →max(min)            (1)

 

a₁₁ X₁ + a₁₂ X₂ +…a_1n X _n   ≤ b_1,

а₂₁ X₁ + a₂₂ X₂ +…a_2n X _n   ≤ b₂                                                    (2)

a_m1 X₁ + a_m2 X₂ +…a _mn X _n   ≤ b _m,

 

X₁≥0 X₂≥0 X₃≥0 …X _n ≥0

 

Этапы решения поставленной задачи симплексным методом включают:

       1) Составление нулевого опорного плана. Вводим новые неотрицательные (базисные) переменные, благодаря которым система неравенств (2) становится системой уравнений:

a₁₁ X₁ + a₁₂ X₂ +…a_1n X _n  + X_n+1 = b₁

a₂₁ X₁ + a₂₂ X₂ +…a_2n X _n  + X_n+2  = b₂                                                  (3)

……………………………………..

a_m1 X₁ + a_m2 X₂ +…a _mn X _n + X_n+m = b _m,

 

       Если принимать вводимые переменные за векторы-столбцы, то они представляют собой единичные (базисные) векторы. Отметим, что базисные переменные имеют простой физический смысл – это остаток конкретного ресурса на складе при заданном плане выпуска продукции, поэтому данный базис называют естественным. Решаем систему (3) относительно базисных переменных:

 

X_n+1    = b_1, -a₁₁ X₁ - a₁₂ X₂ -…a_1n X _n

X_n+2    = b₂  - a₂₁ X₁ - a₂₂ X₂ -…a_2n X _n                                   (4) 

………………………………………..

X_n+m = b _m, - a_m1 X₁ + a_m2 X₂ +…a _mn X _n

 

Целевую функцию перепишем в виде

Z(X) = 0-(-с₁Х₁-с₂Х₂-с₃Х₃-…-с_nХ_n)                                (5)

 

       Полагая, что искомые основные переменные Х₁ = X₂ = X₃ = … = X_n = 0, получаем нулевой опорный план Х = (0, 0, …0, b₁, b_2, b_{3 …} b_m ), при котором Z(X) = 0 (все ресурсы на складе, ничего не производится). Заносим план в симплексную таблицу.

 

План	Базис	Ci/Cj	Знач. Xi	X1	X2	Xn	Xn+1	Xn+2	Xn+3	Qmin
0	Xn+1	0	b1	a11	a12	a13	1	0	0	b1/ a12
	Xn+2	0	b2	a21	a22	a23	0	1	0	b2/ a22
	Xn+3	0	b3	a31	a32	a33	0	0	1	b3/ a32
Z(X) = 0				-C1	- C2	- C3	0	0	0	Индекс. строка

 

       2) Из отрицательных коэффициентов индексной строки выбираем наибольший по абсолютной величине, что определяет ведущий столбец и показывает – какая переменная на следующей итерации (шаге) перейдет из основных (свободных) в базисные (фактически выбирается товарная группа, чья реализация приносит максимальный доход). Затем запасы сырья b_i делим на соответствующие коэффициенты затрат, результаты заносим в таблицу и определяем минимальное значение Q_min (выбирается ресурс, чей запас наиболее сильно ограничивает выпуск выбранной товарной группы). Это значение выделяет ведущую строку и переменную Х_i , которая при следующем шаге (итерации) выйдет из базиса и станет свободной.

 

       3) Переход к новому плану осуществляется в результате пересчета симплексной таблицы методом Жордана-Гаусса. Сначала заменим в базисе Х_j на Х_i ведущего столбца. Разделим все элементы ведущей строки на разрешающий элемент (РЭ), в результате чего на месте РЭ в ведущей строке будет 1. Так как Х_i стал базисным, то остальные его коэффициенты должны быть равны 0. Новые элементы этого плана находятся по правилу прямоугольника

НЭ=СЭ – (А*В)/РЭ                                          (6)

 

       Оценка полученного плана производится по коэффициентам индексной строки: если они все положительны, то план оптимален, если нет, то план можно улучшить, производя следующую итерацию (шаг).

    

Пример. На приобретение оборудования для производственного участка выделено 20 тыс.руб. Оборудование может быть размещено на площади, не превышающей 72 кв.м. Можно заказать оборудование двух типов: типа А, требующие производственную площадь 6кв.м и дающие 6 тыс.ед. продукции в смену ( цена 5000 руб.) и типа В, требующие площадь 12 кв.м и дающие 3тыс.ед., (цена 2000 руб.). Каков оптимальный план приобретения оборудования, обеспечивающий максимальную производительность участка?

  Обозначим количество приобретаемого оборудования типа А и В через Х₁ и Х₂ соответственно.

Производительность участка (целевая функция) : Z(X) =6Х₁+3Х₂.

Основные ограничения связаны

с денежными средствами : 5Х₁+2Х₂ ≤ 20,

с площадью производственного участка : 6Х₁+12Х₂ ≤ 72.

Вводим новые базисные переменные Х₃ (остаток денежных средств после закупки оборудования) и Х₄ (остаток площадей после размещения оборудования) и перепишем ограничения в виде системы уравнений:                        

                            5X₁+2Х₂+X₃=20      (X₃=20 – 5X₁ - 2X₂)

                            6Х₁+12Х₂+X₄ = 72  (X₄=72 – 6X₁ – 12X₂)

При этом функция цели: Z(X) =6Х₁+3Х₂+0Х₃+0Х₄.

Составляем опорный (0-ой) план: Х= (0, 0, 20, 72), т.е. пока ничего не приобретено (деньги не потрачены, площади пустуют). Составляем симплексную таблицу

План	Базис			Ci/Cj	Знач. Xi		X1	X2	X3	X4	Qmin
0	X3			0	20		5	2	1	0	20/5=4
	X4			0	72		6	12	0	1	72/6=12
Z(X) = 0							- 6	- 3	0	0	Индексная строка
1		→X1	6			4	1	0,4	0,2	0	4/0,4=10
		X4	0			48	0	9,6	-1,2	1	48/9,6=5
Z(X) = 6*4=24							0	-0,6	1,2	0	Индексная строка
2		X1	6			2	1	0	0,25	-1/24	-
		→X2	3			5	0	1	-1/8	5/48	-
Z(X) =6*2+3*5=27							0	0	9/8	1/16	Индексная строка

 

Очевидно, что ведущий столбец соответствует Х₁, так как имеет самый большой индекс 6. Находим минимальное значение Q_min = 4 ( самое жесткое ограничение ресурса), определяя ведущую строку, показывающую, что из базисных переменных выводится Х₃, а вместо нее вводится Х₁. Пересчитываем элементы ведущей строки, разделив их на 5, а по формуле (6) определяем элементы второй и индексной строк. Целевая функция для 1-ого плана равна Z(X) = 6*4+3*0 = 24.

Однако, один из коэффициентов индексной строки для столбца Х₂ остается отрицательным -0,6, следовательно данный план не оптимален, и требуется еще одна итерация (шаг) для его улучшения. Выбираем ведущим 2-ой столбец и по минимальному значению Q_min = 5 определяем ведущую строку с базисной переменной Х₄. Выполнив те же преобразования, получаем 2-ой план, который будет оптимальным, так как все индексные коэффициенты положительны.

Проанализируем полученные результаты. При оптимальном решении целевая функция имеет максимальное значение 27тыс.руб., при этом оба ресурса выведены из базиса, следовательно израсходованы полностью.

Убедимся в этом: 5*2+2*5 = 20 тыс.руб., 6*2+12*5=72 кв.м. Искомое решение Х= (2; 5;0;0).Так бывает далеко не всегда.

 

Лекция № 10

Тема: Закрытая транспортная задача

План:

1. Математическая формулировка закрытой транспортной задачи. Определение необходимого количества неизвестных.

2. Этапы определения плана решения транспортной задачи.

 

Обозначения:

m – количество пунктов отправления (поставщиков);

i – номер поставщика;

n – количество пунктов назначения (потребителей);

j – номер потребителя;

a_i – объем однородного груза i-го поставщика (запасы);

b_i – объем однородного груза, требуемого j-ому потребителю (спрос);

c_ij – стоимость доставки единицы груза i-го поставщика j-ому потребителю;

x_ij – количество груза, доставляемое от i-го поставщика к j-му потребителю;

С – общие затраты на перевозки.

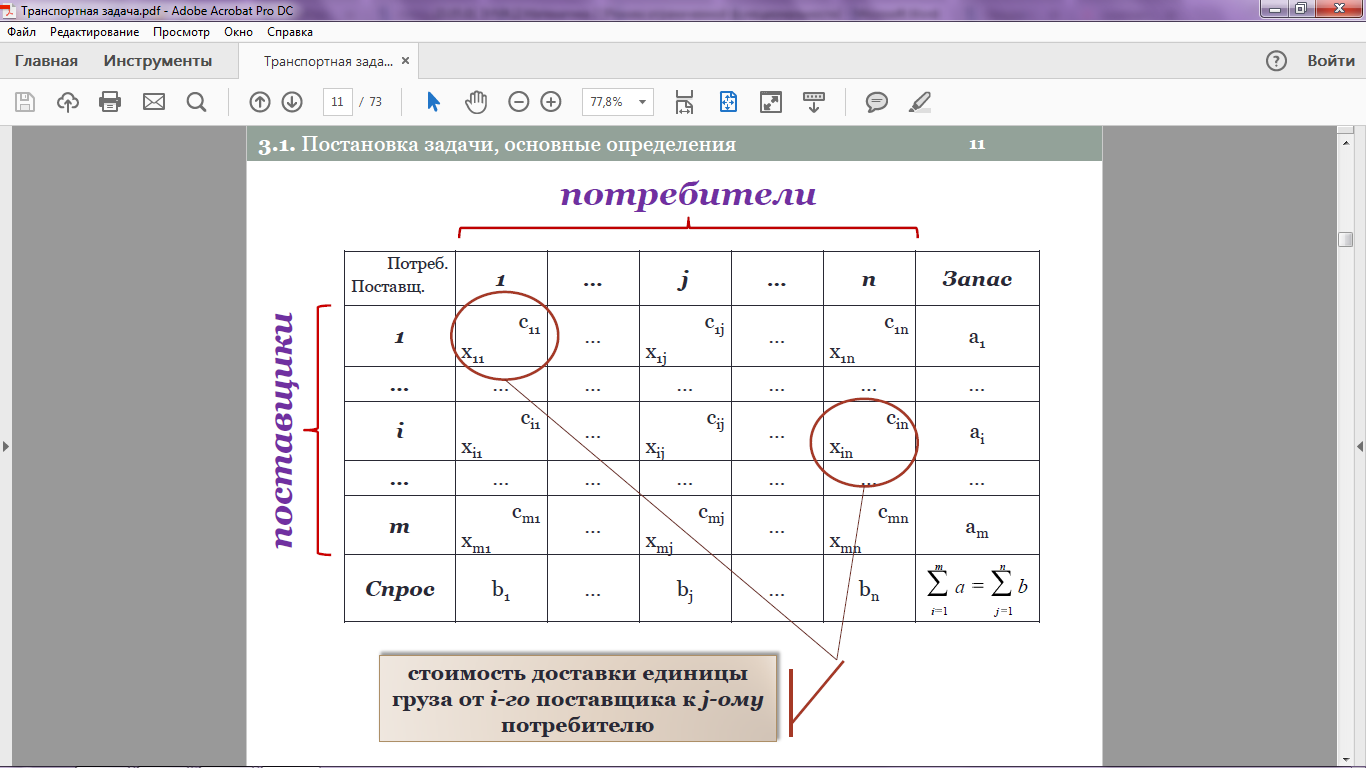
Пусть в пунктах (поставщиках) 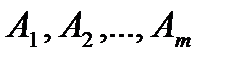 сосредоточен однородный груз (сено, ё

картофель и т.д.) в количествах соответственно 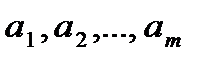, который необходимо перевезти  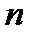потребителям  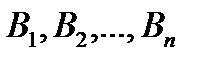в количествах 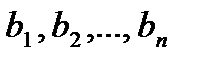. Известны транспортные расходы (тарифы) 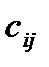, по перевозке единицы груза от поставщика  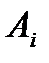к потребителю 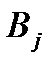. Требуется составить план перевозки груза, по которому:

1) груз от каждого поставщика должен быть вывезен;

2) спрос каждого потребителя полностью удовлетворен;

3) затраты на перевозку должны быть минимальными.

Необходимое и достаточное условие решения поставленной задачи состоит в том, чтобы суммарный запас груза был бы равен суммарному спросу на него, то есть 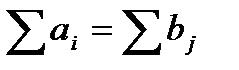. Если это условие выполнено, то соответствующая ТЗ носит название задачи с закрытой моделью.

Условия транспортной задачи можно записать в виде распределительной таблицы 1, где указаны поставщики 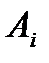 и запасы груза у них 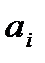, потребители  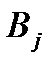и их потребность в грузе 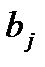, стоимость перевозок единицы груза 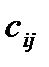, из пункта  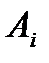в пункт 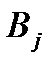.                                                                                                                                                                         Таблица 1

Поставщик

Потребители

Запас груза

…………… …………… …………… …………… ……………   …………… …………… …………… Потребность в грузе ……………

 

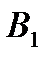
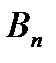
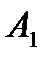
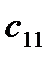
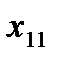
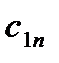
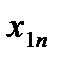
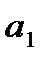
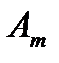
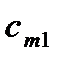
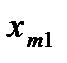
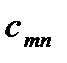
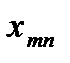
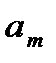
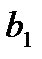
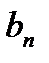
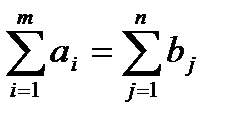
В клетках этой же распределительной таблицы можно составить план перевозок груза 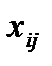 из пункта  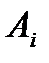в пункт 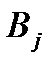.                                                                                                                                        При этом расходы на перевозку груза составят:

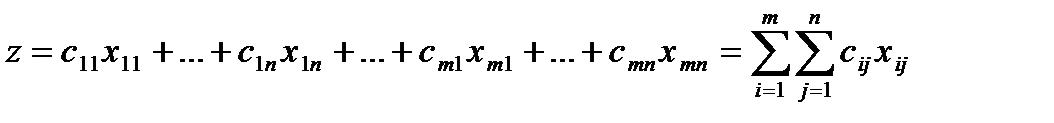                              (1)

Таким образом, математическая формулировка ТЗ следующая: Найти 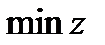, если переменные  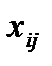удовлетворяют условиям:

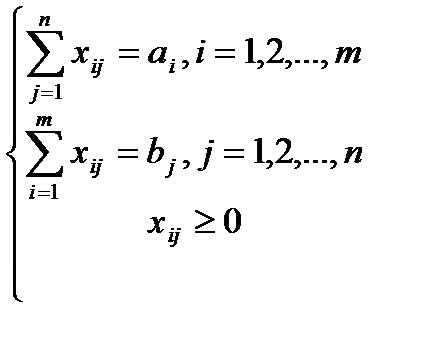                                               (2) 

 Система ограничений (2) состоит из 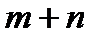 уравнений, в которых содержится  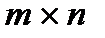переменных. В теории ТЗ доказывается, что ранг матрицы системы (2) равен  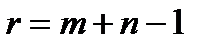и поэтому опорный план решения задачи содержит  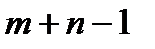базисных переменных, остальные  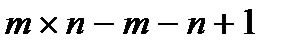переменные являются свободными и в опорном плане принимают значения равные нулю.

 

2. Этапы определения плана решения транспортной задачи .

При составлении опорного плана решения задачи в распределительной таблице 1 будут заполнены не более 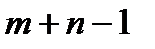 клеток, остальные клетки будут свободными (пустыми), так как соответствующий им груз равен нулю.

Таким образом, план решения ТЗ может быть определен следующими этапами:

1. Построение опорного плана решения ТЗ (в распределительной таблице заполняются не более 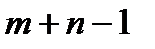 клеток).

2. Проверка опорного плана на оптимальность.

3. Улучшение опорного плана, если он не оптимальный.

4. Проверка улучшенного плана на оптимальность. Процесс заканчивается оптимальным планом.

Рассмотрим каждый этап решения ТЗ.

 

1. Построение опорного плана решения ТЗ.

Рассмотрим два метода построения опорного плана.

а) Метод «Северо-западного угла»

       Суть этого метода состоит в том, что заполнение распределительной таблицы ТЗ начинается с левого верхнего угла (клетка 1;1). В ней записывается максимально возможный груз: 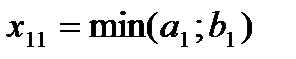. Например, если 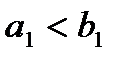, то 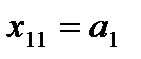 и весь груз из пункта  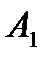вывезен в пункт 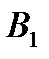, но в  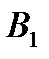надо завозить еще  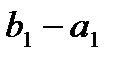единицу груза. Этот недостающий груз завозим из пункта 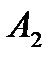, записывая в клетку (2;1) максимально возможный груз 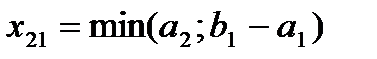. Заполнив клетку (2;1), заполняем следующую, либо в той же строке 2 (если 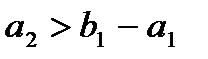), либо в строке 3 (если 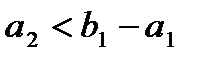). Последней заполняется клетка 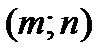. При этом число заполненных клеток будет не более 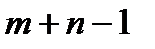.Пример построения опорного плана методом «Северо-западного угла» приведен для следующей задачи .

   Задача №1.

Фирма, выпускающая газированные напитки, складируемые в трех разных местах, должна поставить продукцию в четыре супермаркета. Каждая упаковка содержит 20 бутылок по 1,5 литра, тарифы на доставку товара, объемы запасов и заказы на продукцию приведены в табл. 2.

 

       Таблица 2. Результаты расчетов.

Поставщики	Потребители				Запасы груза
	6 75	7 25	3	5	100
	1	2 55	5 60	6 35	150
	2	10	20	2 50	50
Потребность в грузе	75	80	60	85	300

 

Затраты на перевозку 300 ед. груза по этому плану составляют:

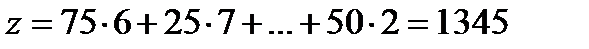 (у.е.)

б) Метод «Минимального элемента»

Опорный план, построенный по методу «Северо-западного угла» обычно оказывается далеким от оптимального, так как при его составлении игнорируются величины затрат 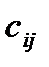. Поэтому существуют другие методы составления начального опорного плана. Простейший из них - метод «Минимального элемента». В отличие от метода «Северо-западного угла», здесь заполнение распределительной таблицы начинается из клетки, у которой наименьший тариф. В эту клетку заносится максимально возможный груз. При этом либо строка, либо столбец окажутся заполненными. Далее заполняется следующая клетка (строки или столбцы), имеющая наименьший тариф.

Пример построения опорного плана методом «Минимального элемента» приведен в табл. 3.

 

Таблица 3. Результаты расчетов.

Поставщики	Потребители				Запасы груза
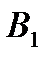
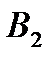
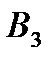
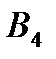
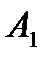
	6	7 5	3 60	5 35	100
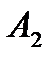
	1 75	2 75	5	6	150
	2	10	20	2 50	50
Потребность в грузе	75	80	60	85	300

 

Здесь порядок заполнения клеток следующий:

.

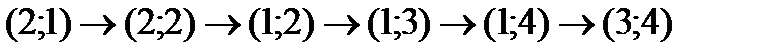Затраты по этому маршруту перевозок составят: 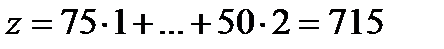 (у.е.). Мы видим, что по этому плану затраты на перевозку груза значительно меньше 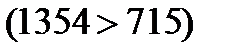. И в таблице 2 и в таблице 3 заполненных клеток оказалось 3 + 4 - 1 = 6.

 

2. Проверка опорного плана на оптимальность.

Будем проверять опорный план на оптимальность методом потенциалов. Суть его состоит в том, что каждой строке и столбцу распределительной таблицы приписываются некоторые числа 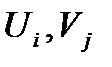 называемые потенциалами. Таким образом, числа  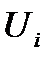- потенциалы строк,  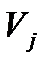- потенциалы столбцов. Эти числа рассчитываются по формуле: для каждой заполненной клетки распределительной таблицы сумма потенциалов строки и столбца равна тарифу соответствующей заполненной клетки, то есть

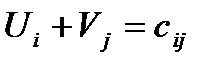.         (3)

Так как заполненных клеток не более 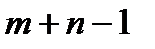, а число всех потенциалов строк и столбцов равна 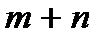, то в системе уравнений (3) имеется  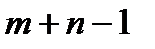уравнений с  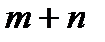неизвестными и она имеет бесконечно много решений. В этом случае одной из неизвестных можно дать определенное значение и тогда система будет иметь единственное решение. Обычно потенциал первой строки считают равным нулю ( 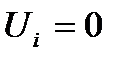) и далее по этому потенциалу и по заполненным клеткам первой строки находят потенциалы соответствующих столбцов, а по заполненным клеткам столбцов, находят потенциалы других строк.

Вычислив, таким образом, потенциалы строк и столбцов, вычисляем характеристики свободных клеток распределительной таблицы по формуле: 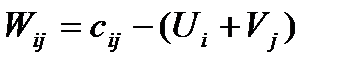. Отрицательные характеристики каких-то свободных клеток указывают на их перспективность: в этих клетках тарифы малы и их заполнение приведет к улучшению плана перевозок. Итак, если хотя бы одна свободная клетка будет иметь отрицательную характеристику, то план является не оптимальным и его надо улучшать.

Замечание. Методика вычисления потенциалов строк и столбцов существенным образом опирается на то, что заполнено ровно 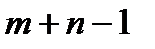 клеток. Если заполненных клеток будет меньше, чем  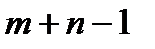(такой план называется вырожденным), то при расчете потенциалов в необходимое количество пустых клеток записывают нуль груза и считают их заполненными.

 

3. Алгоритм улучшения неоптимального плана.

Переход к лучшему плану осуществляется с помощью перераспределения груза и заполнения клетки с отрицательной характеристикой. Если таких клеток несколько, то выбирают ту, в которой отрицательная характеристика оказалась самой большой по абсолютной величине. Перераспределение груза происходит по замкнутому маршруту (контуру), который строится по следующей схеме:

1) Маршрут начинается и заканчивается в клетке с отрицательной характеристикой;

2) Линии контура строго вертикальны или горизонтальны (нельзя двигаться по диагонали);

3) Повороты (на 90⁰) можно осуществлять только в заполненных клетках.

После построения замкнутого маршрута (самый простой вариант – прямоугольник), происходит перераспределение груза (улучшение опорного плана) по следующей схеме:

4) Каждой угловой клетке маршрута (где осуществлялись повороты на 90⁰) присваивается знак «+» или «-», причем клетке, из которой начинается маршрут, приписывают знак «+», далее знаки чередуются;

5) Среди клеток со знаком «-» выбирают клетку с наименьшим грузом;

6) Наименьший груз прибавляют ко всем клеткам со знаком «+» и вычитают из всех клеток со знаком «-». При этом пустая клетка, из которой начиналось движение и которая имела отрицательную характеристику, становится заполненной, а заполненная клетка, имевшая груз, который подлежал перераспределению, стала пустой.

Далее, улучшенный план вновь проверяют на оптимальность и улучшают до тех пор, пока характеристики всех пустых клеток не окажутся положительными. Это означает, что пустыми оказались клетки с большими тарифами, а заполнены клетки с малыми тарифами и поэтому затраты на перевозку груза оказались минимальными.

Проверим, например, оптимальность плана, построенного методом «Минимального элемента» в таблице 3 (он лучше плана построенного методом «Северо-западного угла» в таблице 2). Для этого рассчитаем потенциалы строк 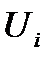 и столбцов  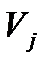по заполненным клеткам табл. 3. Результаты расчетов запишем в таблицу 4

Таблица 4. Результаты расчетов.

Поставщики	Потребители				Потенциалы строк
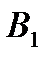
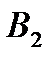
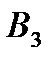
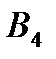
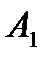
	6	«-» 7 5	3 60	«+» 5 35	0
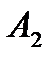
	«-» 1 75	2 75 «+»	5	6	- 5
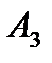
	2 «+»	10	20	2 50 «-»	- 3
Потенциалы столбцов	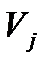6	7	3	5

 

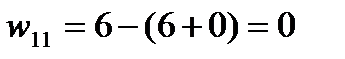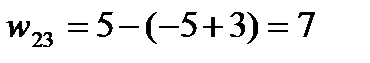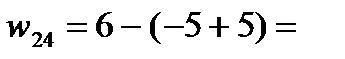
Теперь по таблице 4 рассчитаем характеристики свободных клеток. Имеем, ; ; ; ; 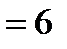; 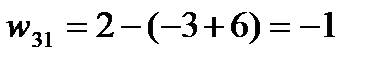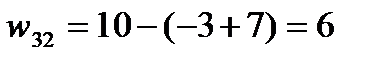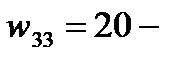(-3+3)=20.Таким образом, среди свободных клеток одна клетка (3;1) имеет отрицательную характеристику .

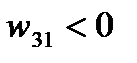     По описанной выше схеме строим маршрут перераспределения груза. Движение начинаем из клетки (3;1) и ей присваиваем знак «+». Далее знаки чередуются. Среди клеток со знаком «-» наименьший груз (равный 5 ед.) в клетке (1;2). Этот груз мы вычитаем из клеток (1;2), (2;1), (3;4) и прибавляем в клетки со знаком «+» (3;1), (1;4), (2;2).

Таблица 5. Результаты расчетов.

Поставщики	Потребители				Запасы груза
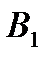
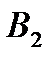
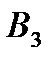
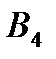
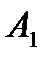
	6	7	3 60	5 40	100
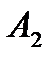
	1 70	2 80	5	6	150
	2 5	10	20	2 45	50
Потребность в грузе	75	80	60	85	300

Получаем новый опорный план (таблица 5).

Затраты по новому плану составят 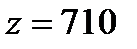 (у.е.). Проверка этого плана показывает, что он оптимальный.

Замечание. Если в опорном плане оказалось несколько клеток с отрицательной характеристикой, то маршрут перераспределения начинается из клетки с самой большой по абсолютной величине отрицательной характеристикой.

 

 

Лекция № 1

Тема : Алгебра событий

План:

1. События, их классификация, вероятность события.

2. Операции над событиями.

3. Непосредственные вычисления вероятности (классический, геометрический, статистический метод).

4. Теорема сложения и умножения вероятностей.

5. Формула Бернулли. Формулы полной вероятностей и Байеса.

6. Локальная и интегральная теорема Лапласа.

1. События, их классификация, вероятность события.

       Событием называется всякий факт, который может произойти или не произойти в результате опыта.

       При этом тот или иной результат опыта может быть получен с различной степенью возможности. Т.е. в некоторых случаях можно сказать, что одно событие произойдет практически наверняка, другое практически никогда.

       В отношении друг друга события также имеют особенности, т.е. в одном случае событие А может произойти совместно с событием В, в другом – нет.

       События называются несовместными, если появление одного из них исключает появление других.

       Классическим примером несовместных событий является результат подбрасывания монеты – выпадение лицевой стороны монеты исключает выпадение обратной стороны (в одном и том же опыте).

       Полной группой событий называется совокупность всех возможных результатов опыта.

       Достоверным событием называется событие, которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта.

       Например, если из коробки, содержащей только красные и зеленые шары, наугад вынимают один шар, то появление среди вынутых шаров белого – невозможное событие. Появление красного и появление зеленого шаров образуют полную группу событий.

       События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей вероятностью.

       В приведенном выше примере появление красного и зеленого шаров – равновозможные события, если в коробке находится одинаковое количество красных и зеленых шаров.

       Если же в коробке красных шаров больше, чем зеленых, то появление зеленого шара – событие менее вероятное, чем появление красного.

Исходя из этих общих понятий можно дать определение вероятности.    Вероятностью события называется число, являющееся выражением меры объективной возможности появления события.

       Очевидно, что вероятность достоверного события равна единице, а вероятность невозможного – равна нулю. Таким образом, значение вероятности любого события – есть положительное число, заключенное между нулем и единицей .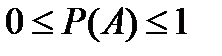

 

Операции над событиями.

       События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот.

 

       Объединением или суммой событий А _k называется событие A, которое означает появление хотя бы одного из событий А _k.

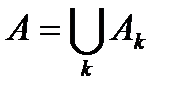
       Пересечением или произведением событий A_k называется событие А, которое заключается в осуществлении всех событий A_k.

 

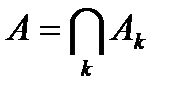
       Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В.

 

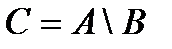
       Дополнительным к событию А называется событие 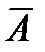, означающее, что событие А не происходит.

       Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают друг друга и в результате опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие.

       Совокупность всех элементарных исходов опыта называется пространством элементарных событий.

 

3. Непосредственные вычисления вероятности (классический, геометрический, статистический метод).

Классический метод определения вероятности.

Для количественного сравнения событий по степени возможности их появления вводится числовая мера, которая называется вероятностью события.

       Вероятность события А равна отношению числа случаев т, благоприятствующих ему, к числу п - общму числу случаев (единственно возможных, равновозможных и несовместных). Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А:

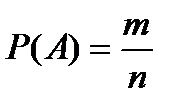 - классическое определение вероятности.

Это есть Из формулы следует, что вероятность события является неотрицательным числом и может изменяться в пределах от нуля до единицы в зависимости от того, какую долю составляет благоприятствующее число случаев от общего числа случаев: 0 ≤ т ≤ п, .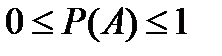

Таким образом, для нахождения вероятности события необходимо, рассмотрев различные исходы испытания, найти совокупность единственно возможных, равновозможных и несовместных случаев, подсчитать общее их число п, число случаев т, благоприятствующих данному событию, и затем выполнить расчет по формуле.

 

Свойства классической вероятности:

1. Если все случаи являются благоприятствующими данному событию 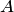, то это событие обязательно произойдет. Следовательно, рассматриваемое событие является достоверным, а вероятность его появления Р(А) = 1, так как в этом случае т = п :

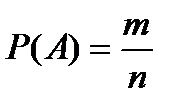= 1

2. Если нет ни одного случая, благоприятствующего данному событию 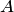, то это событие в результате опыта произойти не может. Следовательно, рассматриваемое событие является невозможным, а вероятность его появления Р(А) = 0, так как в этом случае :

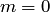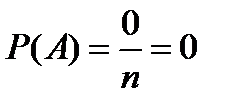
3. Вероятность наступления событий, образующих полную группу, равна единице.

4. Вероятность наступления противоположного события, которое обозначается символом 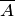, определяется:

 

Р(А)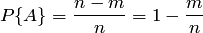

где 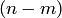 - число случаев, благоприятствующих появлению противоположного события 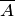. Отсюда вероятность наступления противоположного события  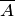равна разнице между единицей и вероятностью наступления события :

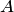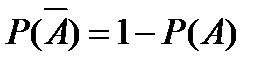
       Важное достоинство классического определения вероятности события состоит в том, что с его помощью вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.

Пример. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.

Решение. Обозначим 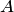 событие, состоящее в том, что набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных исходов равно 10. Эти исходы единственно возможны (одна из цифр набрана обязательно) и равновозможны (цифра набрана наудачу). Благоприятствует событию  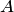лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех исходов:

.

 

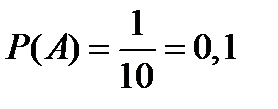       Пример. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет красным, зеленым или белым.

       Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С.

       Тогда в соответствием с записанными выше формулами получаем:

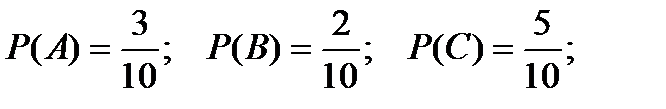
       Отметим, что вероятность наступления одного из двух попарно несовместных событий равна сумме вероятностей этих событий.

       Но классический метод определения вероятности случайного события довольно относительный, так как на практике сложно представить результат опыта в виде совокупности элементарных событий, доказать, что события равновероятные.

       Например, при произведении опыта с подбрасыванием монеты на результат опыта могут влиять такие факторы как несимметричность монеты, влияние ее формы на аэродинамические характеристики полета, атмосферные условия и т.д.

       Классический метод определения вероятности неприменим к испытаниям с бесконечным числом исходов по двум причинам: во-первых, классическое определение вероятности предполагает, что общее число случаев 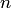 должно быть конечно. На самом же деле оно зачастую не ограничено. Во-вторых, часто невозможно представить исходы опыта в виде равновозможных и несовместных событий.

       Следовательно, необходимо использовать другие методы вычисления вероятностей.

 

Геометрический метод определения вероятности.

Введем понятие геометрической вероятности, т.е. вероятности попадания точки в какой – либо отрезок или часть плоскости (пространства).

Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве).

Элементарные исходы – это отдельные точки G, любое событие – это подмножество этой области, пространства элементарных исходов G. Можно считать, что все точки G «равноправны» и тогда вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы.

Таким образом, в общем случае, если возможность случайного появления точки внутри некоторой области на прямой, плоскости или в пространстве определяется не положением этой области и ее границами, а только ее размером, т. е. длиной, площадью или объемом, то вероятность попадания случайной точки внутрь некоторой области определяется как отношение размера этой области к размеру всей области, в которой может появляться данная точка. Это есть геометрическое определение вероятности .

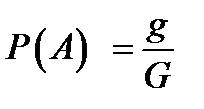
где 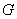 – геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а  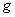– мера, выражающая количество благоприятствующих событию  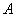исходов. На практике в качестве такой геометрической меры чаще всего выступает длина или площадь, реже объём.

Пример. Пусть на плоскости задана некоторая область 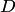 площадью 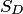, в которой содержится другая область  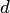площадью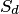

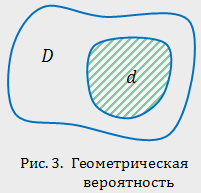
 В область 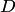 наудачу бросается точка. Чему равна вероятность того, что точка попадет в область 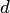? При этом предполагается, что наудачу брошенная точка может попасть в любую точку области 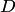, и вероятность попасть в какую-либо часть области  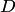пропорциональна площади части и не зависит от ее расположения и формы. В таком случае вероятность попадания в область  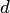при бросании наудачу точки в область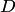

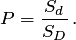
Пример. Круглая мишень вращается с постоянной угловой скоростью. Пятая часть мишени окрашена в зеленый цвет, а остальная — в белый:

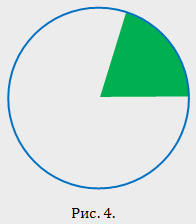
По мишени производится выстрел так, что попадание в мишень — событие достоверное. Требуется определить вероятность попадания в сектор мишени, окрашенный в зелёный цвет.

Решение. Обозначим 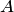 — «выстрел попал в сектор, окрашенный в зелёный цвет». Тогда 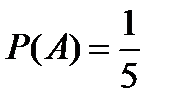. Вероятность получена как отношение площади части мишени, окрашенной в зелёный цвет, ко всей площади мишени, поскольку попадания в любые части мишени равновозможны.

 

Статистический метод определения вероятности.

Введем понятие - частота появления событий W ( A ) _- при многократно повторяющихся опытах имеет тенденцию стабилизироваться около какой-то постоянной величины. Таким образом, с рассматриваемым событием можно связать некоторую постоянную величину, около которой группируются частоты и которая является характеристикой объективной связи между комплексом условий, при которых проводятся опыты, и событием.

       Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов.

       Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного проведения опытов, а относительная частота – после опыта.

       При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа. Это число может быть принято за вероятность события.

Статистической вероятностью случайного события называется число, около которого группируются частоты этого события по мере увеличения числа испытаний (или: число, к которому стремится устойчивая относительная частота):

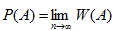
       Пример. если из коробки наугад извлечено 5 шаров и 2 из них оказались красными, то относительная частота появления красного шара равна:

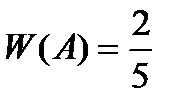
       Как видно, эта величина не будет совпадать с вероятностью события.

 

Преимущество статистического способа определения вероятности состоит в том, что он опирается на реальный эксперимент. Однако его существенный недостаток заключается в том, что для определения вероятности необходимо выполнить большое число опытов, которые очень часто связаны с материальными затратами. Статистическое определение вероятности события хотя и достаточно полно раскрывает содержание этого понятия, но не дает возможности фактического вычисления вероятности.