Известно, что при измерениях физических величин получаются приближенные числовые значения. При этом приближенные числа следует записывать, сохраняя только верные значащие цифры. При подсчете значащих цифр не считаются нули с левой стороны. Поясним это с помощью табл. 1.
Таблица 1
Определение количества значащих цифр
| Приближенное число | Количество значащих цифр | Приближенное число | Количество значащих цифр |
| 5000 | 4 | 3,20 | 3 |
| 5 ∙ 103 | 1 | 3,2 | 2 |
| 0,0107 | 3 |
Например, значение 5000 г получаем при взвешивании тел с точностью до грамма, а 5 ∙ 103 г – при взвешивании с точностью до килограмма. Взвешивание в первом случае было произведено в 1000 раз точнее, чем во втором.
Аналогично число 3,20 означает, что при измерении учитывались в сотые доли, а в числе 3,2 – только десятые, т. е. точность в этом случае в 10 раз меньше. Так бывает, в частности, при измерениях микрометром и штангенциркулем.
При математических действиях приближенные числа округляют, если они содержат лишние значащие цифры. Покажем округление до n значащих цифр числа 6 705, 846 (табл. 2).
Таблица 2
Примеры округления
| Приближенное число | Количество значащих цифр | Приближенное число | Количество значащих цифр |
| 6 705,85 | 6 | 671 ∙ 10 | 3 |
| 6 705,8 | 5 | 67 ∙ 102 | 2 |
| 6 706 | 4 | 7 ∙ 103 | 1 |
Выполняя вычисления, всегда необходимо помнить о той точности, которую можно получить. Приведем правила, при соблюдении которых можно считать, что в среднем полученные результаты будут иметь все знаки верными, хотя в отдельных случаях возможна ошибка в несколько единиц последнего знака.
1. Если некоторые данные содержат больше десятичных знаков (при сложении и вычитании) или больше значащих цифр (при умножении, делении, возведении в степень, извлечении корня), чем другие, то их предварительно следует округлить, сохраняя лишь одну лишнюю цифру.
Примеры
Вместо 1,82 следует сложить 1,82
+ 14,367 3 + 14,37
5,8 5,8
21,987 3 21,99
Вместо 83 937 ∙ 0,4 = 33 577,8 следует перемножить 84 ∙ 103 ∙ 0,4 = 33,6 ∙ 103.
2. При сложении и вычитании приближенных чисел в результате следует сохранять столько десятичных знаков, сколько их в числе с наименьшим количеством десятичных знаков.
Пример
1,82 + 14, 368 3 + 5,8 = 1,82 + 14,37 + 5,8 = 22,0.
3. При умножении и делении в результате следует сохранять столько значащих цифр, сколько их в приближенном числе с наименьшим количеством значащих цифр.
Примеры: 83 973 ∙ 0,4 = 84 ∙103 ∙ 0,4 = 33,6 ∙ 103 = 3 ∙104.
.
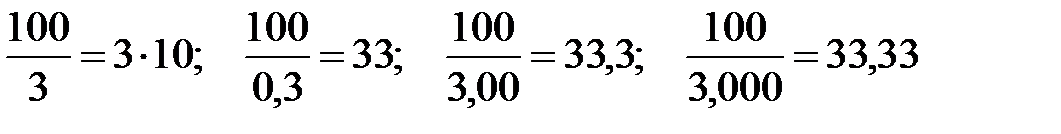4. При возведении в квадрат и клуб в результате следует сохранять столько значащих цифр, сколько их имеет возводимое в степень приближенное число.
Примеры: 1,322 = 1,74; 3,63 = 46.
5. При извлечении квадратного и кубического корней в результате следует брать столько значащих цифр, сколько их в подкоренном приближенном числе.
Примеры: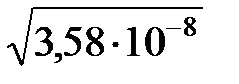 
= 1,89 ∙ 10-4; 
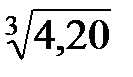= 1,61.
6. При вычислении промежуточных результатов следует брать на одну цифру больше, чем рекомендуют правила. В окончательном результате эта "запасная" цифра отбрасывается.
Пример
.
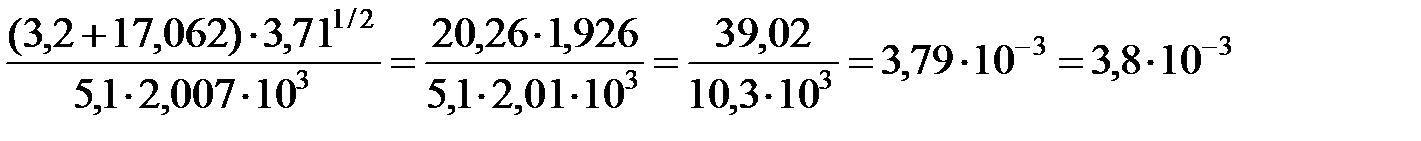В этом примере сомножитель 5,1 имеет наименьшее количество значащих цифр (две). Поэтому и окончательный результат получился с двумя значащими цифрами.
Количество значащих цифр в результате, не может быть увеличено, а его точность не может быть повышена путем искусственного набирания знаков (неверных) при математических действиях. Погрешность результата определяется точностью измерительных приборов, тщательностью исходных прямых измерений.
В студенческой практике абсолютная ошибка окончательного результата округляется до одной значащей цифры, а сам результат до того разряда, в котором находится эта значащая цифра.
Дата: 2019-02-25, просмотров: 225.
