Вид распределения по закону Симпсона, называемому также «законом треугольника». Числовые характеристики погрешностей, распределенных по этому закону, определяют по формулам: М(Δ⁰)=( Δ⁰₁+ Δ⁰₂)/2

σ(Δ⁰)=(Δ⁰₂-Δ⁰₁)/(2√6). Сумма двух случайных погрешностей, распределенных по закону равномерной плотности, подчиняется закону Симпсона.

Например: Если при измерении временного интервала цифровым методом если начало измеряемого интервала не синхронизировано с последовательностью счетных импульсов (рис. 2б), то при отсутствии синхронизации начало интервала может с одинаковой вероятностью попасть в интервал времени от нулевого до первого счетного импульса. Эта погрешность подчинена равномерному закону с предельными значениями 0 и Т₀ Если интервал Т_к не измерен, то случайные погрешности независимы, а закон распределения общей погрешности дискретизации треугольный с предельными значениями ±Т₀. Другие примеры:ошибка суммирования двух округленных величин распределена по закону треугольника; если отклонения размеров отверстия распределены в пределах допусков равномерно, то зазоры или натяги в пределах допуска будут распределены по закону треугольника и т.д.

33. Нормальное распределение погрешностей измерений (распределение Гаусса).

На практике наиболее часто (примерно в 30% измерений) встречается нормальный закон распределения погрешностей. Основываясь на положениях теории вероятностей, можно сделать вывод, что сумма достаточно большого числа независимых случайных погрешностей, подчиненных каким-либо законам распределения, при отсутствии явного доминирования одной или нескольких погрешностей над другими, подчиняется нормальному закону. Поэтому он является предельным законом для суммы независимых случайных погрешностей.

Практически при суммировании двух и более случайных погрешностей, распределенных по закону Симпсона, или четырех и более — по закону равномерной плотности, суммарное рассеивание подчиняется нормальному закону. При большом числе измерений вероятность появления случайных погрешностей, как сказано выше, в большинстве случаев подчиняется нормальному закону, симметричному относительно точки, соответствующей максимальной плотности вероятности y=f (Δ⁰). Эта точка соответствует истинному (среднему) значению измеряемой величины x_ист (при наличии систематических погрешностей x_ист может быть не равно измеряемой величине). Если перенести ось ординат в точку математического ожидания, то это будет кривая распределения величины Δ⁰ = x - x_ист , т.е. кривая распределения случайных погрешностей (₃>₂>₁).

Нормальный закон распределения случайных погрешностей имеет вид  где у — плотность вероятности для определенного значения; Δ⁰— значение случайной погрешности;  — среднее квадратическое отклонение. Широкое распространение нормального закона распределения согласно центральной предельной теореме теории вероятностей объясняется тем, что рассеивание значений измеряемых величин вызывается множеством случайных факторов.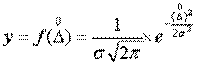

Примечания:

1. Оценки, которые используются вместо истинных результатов показаний, называются точечными и выбор их неоднозначен. Предпочтительны те оценки, которые, во-первых, сходятся к оцениваемому значению (при n) — состоятельные оценки, во-вторых, у которых математическое ожидание равно оцениваемому значению — несмещенные оценки, в-третьих, у которых выборочное распределение имеет наименьшую дисперсию—эффективные оценки.

2. Наряду с точечными широко применяются интервальные оценки числовых характеристик случайных величин, выражающиеся границами интервала, внутри которого с определенной вероятностью заключено истинное значение результата измерений.