Прежде чем применять итерационные методы для решения какой-либо системы, необходимо убедиться, что решение может быть получено, т.е. итерационный процесс сходится к точному решению.
Доказывается теорема, что, если хотя бы одна из норм матрицы нормальной системы (2.3-2.4) меньше единицы, то итерационный процесс сходится к единственному решению. Т.е. изложенные выше итерационные методы можно использовать для систем, удовлетворяющих одному из следующих условий:
Или, для системы (2.1-2.2) итерационный процесс сходится, если элементы матрицы А удовлетворяют условию
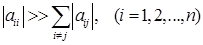
т.е. модули диагональных элементов каждой строки больше суммы модулей всех остальных элементов. Это условие еще называют условием преобладания диагональных элементов.
Метод Якоби (метод простых итераций)
Найти решение системы линейных алгебраических уравнений методом Якоби.
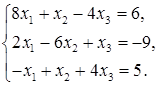
Прежде всего, убеждаемся, что изложенные выше итерационные методы можно использовать для заданной системы, т.к. выполняется условие «преобладания диагональных коэффициентов», что обеспечивает сходимость этих методов.
Приведем эту систему к нормальному виду:
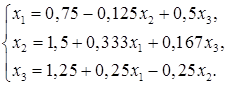
Не составит труда проверка сходимости итерационного процесса по формулам.
1.
 |
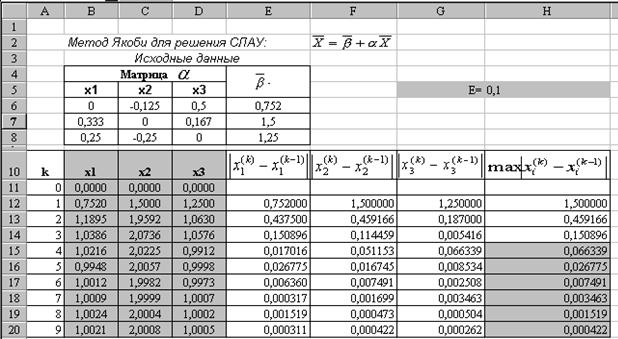Возьмем чистый лист Excel. Заготовим таблицу, как показано на рис.2.1.
Рис.6
2. Исходные данные, матрицы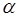 
и 
, введем в ячейки В6:Е8. Значение e - в ячейку Н5. Номер итерации k сформируем в столбце А с помощью автозаполнения. В качестве нулевого приближения выберем нулевой вектор (или вектор свободных членов) и введем его в ячейки В11: D 11.
3. В ячейках В12: D 12 запишем формулы для вычисления первого приближения, используя выражение (2.4). Эти формулы имеют вид:
B12=$E$6 + B11*$B$6 + C11*$C$6 + D11*$D$6,
C12=$E$7 + B11*$B$7 + C11*$C$7 + D11*$D$7,
D12=$E$8 + B11*$B$8 + C11*$C$8 + D11*$D$8.
Эти формулы можно записать иначе, используя функцию Excel СУММПРОИЗВ (см. пример 1.2)
4. В ячейку Е12 введем формулу: E12=ABS(B11-B12) и скопируем ее вправо, в ячейки F12:G12.
5. В ячейку Н12 введем формулу для вычисления M(k) H 12=макс(E12:G12). Выделим ячейки В12:Н12 и скопируем их вниз до конца таблицы. Таким образом, получим k приближений решения СЛАУ.
Анализируя результаты, принимаем за приближенное решение исходной системы с заданной точностью четвертую итерацию, т.е.
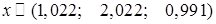
6. Исследуем характер итерационного процесса. Для этого выделим блок ячеек А10: D 20 и построим графики, отражающие сходимость итерационного процесса, используя Вставка→Точечная. Приведенные графики подтверждают сделанный ранее вывод о сходимости итерационного процесса.
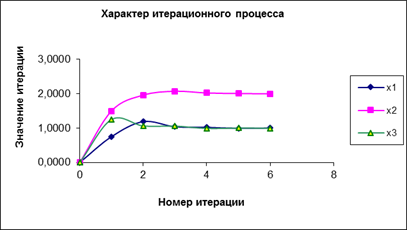
Рис.7
Метод Гаусса-Зейделя.
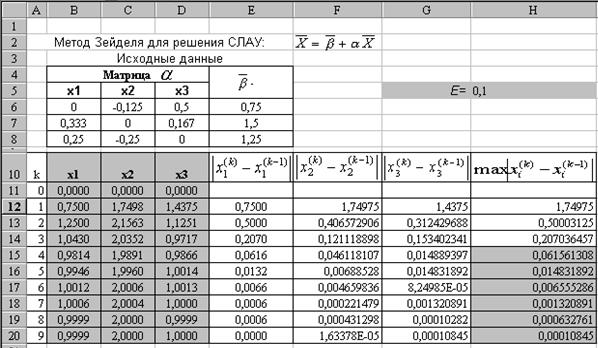
1. Заготовим таблицу на новом листе Excel как показано на рис.2.4.
2.
 |
В качестве нулевого приближения выберем нулевой вектор
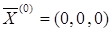и введем его в ячейки В11: D 11.
Рис.8
3. В ячейках В12: D 12 запишем формулы для вычисления первого приближения, используя (2.9). Эти формулы имеют вид:
B12=$E$6 + B11*$B$6 + C11*$C$6 + D11*$D$6,
C12==$E$7 + B12*$B$7 + C11*$C$7 + D11*$D$7,
D12==$E$8 + B12*$B$8 + C12*$C$8 + D11*$D$8.
4. В столбце Н сформируем вычисление M(k) , используя выражение, так, как это проделали в предыдущем примере
Анализируя результаты, принимаем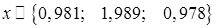 
за приближенное решение исходной системы с заданной точностью.
Дата: 2019-02-25, просмотров: 253.
