Основы численных методов
Методическое пособие для студентов
Заочной формы обучения по направлению
«Информатика и вычислительная техника»
Березники, 2018
Составитель: старший преподаватель Н.Я. Захарова.
Основы численных методов. Методическое пособие для студентов заочной формы обучения по направлению «Информатика и вычислительная техника»/ Сост. Н.Я.Захарова; Перм. нац. исслед. политехн. ун–т. – Березники, 2018. – 25 с.
В пособии рассмотрено решение типовых заданий. Предложено 20 вариантов для контрольной работы.
© Пермский национальный
исследовательский
политехнический университет, 2018
Список литератур ы
1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Наука, 2006.
2. Березин И.С., Жидков Н.П. Методы вычислений. Т.1. – М.: Физматгиз, 1962.
3. Вержбицкий В.М. Основы численных методов. – М.: Высшая школа, 2001.
4. Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике. – М.: Высшая Школа, 1990.
5. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах в 2-х ч. – М.: Высшая школа, 1999.
6. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1970.
7. Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математике. – М.: Высшая школа, 1994.
8. Турчак Л.И. Основы численных методов. – М.: Наука, 1987.
Тема1. Решение уравнений
Задание 1. Отделить корни графически и уточнить любой корень с точностью до 0,001 методом деления пополам.
№ 1. 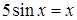 ; (кроме х=0) № 2.
; (кроме х=0) № 2. 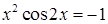 ;
;
№ 3. 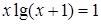 ; № 4.
; № 4. 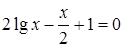 ;
;
№ 5. 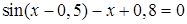 ; № 6.
; № 6. 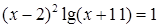 ;
;
№ 7. 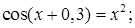 № 8.
№ 8. 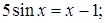
№ 9.  (кроме х=0) № 10.
(кроме х=0) № 10. 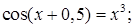
№ 11. 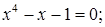 № 12.
№ 12. 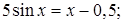
№ 13. 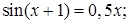 № 14.
№ 14. 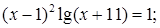
№ 15. 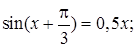 № 16.
№ 16. 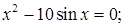 (кроме х=0)
(кроме х=0)
№ 17. 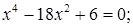 № 18.
№ 18. 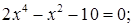
№ 19. 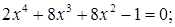 № 20.
№ 20. 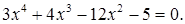
Образец выполнения задания. Найти один корень 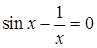 .
.
Перепишем уравнение в виде 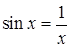 и построим графики левой и правой частей в Excel, изменяя х от 0,5 до 3 с шагом 0,5. В первой строке вводим значения переменной, во второй и третьей – вычисляем значения функций. Используем инструмент «вставка – точечная» для построения графиков.
и построим графики левой и правой частей в Excel, изменяя х от 0,5 до 3 с шагом 0,5. В первой строке вводим значения переменной, во второй и третьей – вычисляем значения функций. Используем инструмент «вставка – точечная» для построения графиков.
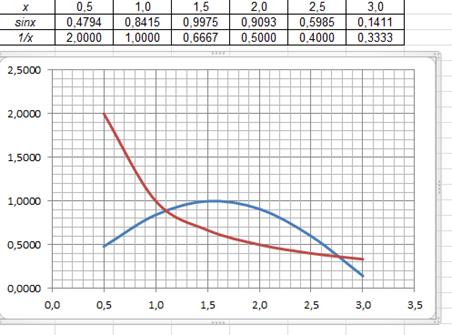
Рис. 1
Уточним корень на отрезке [1;2]. Для этого составим таблицу:
Таблица1
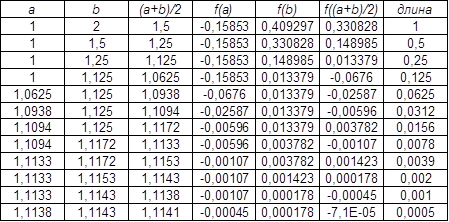
Длина последнего отрезка меньше 0,001, поэтому корень приближенно равен его середине, то есть 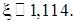
Задание 2. Отделить корни графически и уточнить с точностью до 0,001 больший корень обоих уравнений методами хорд и Ньютона.
№ 1. 1) 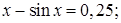 2)
2) 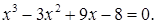
№ 2. 1) 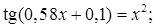 2)
2) 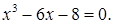
№ 3. 1) 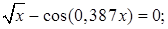 2)
2) 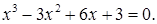
№ 4. 1) 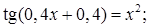 2)
2) 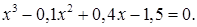
№ 5. 1) 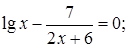 2)
2) 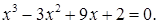
№ 6. 1) 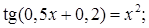 2)
2) 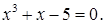
№ 7. 1) 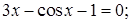 2)
2) 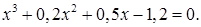
№ 8. 1) 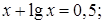 2)
2) 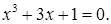
№ 9. 1) 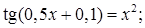 2)
2) 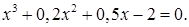
№ 10. 1) 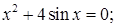 2)
2) 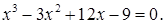
№ 11. 1) 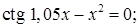 2)
2) 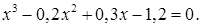
№ 12. 1) 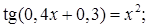 2)
2) 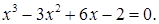
№ 13. 1) 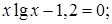 2)
2) 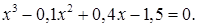
№ 14. 1) 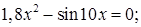 2)
2) 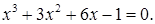
№ 15. 1) 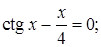 2)
2) 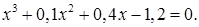
№ 16. 1) 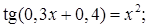 2)
2) 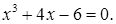
№ 17. 1)  2)
2) 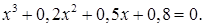
№ 18. 1) 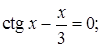 2)
2) 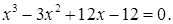
№ 19. 1) 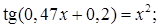 2)
2) 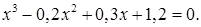
№ 20. 1) 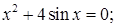 2)
2) 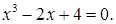
Образец выполнения задания. Найти один корень 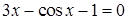 .
.
Перепишем уравнение в виде 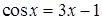 и построим графики левой и правой частей в Excel, изменяя х от -2 до 2 с шагом 0,5. В первой строке вводим значения переменной, во второй и третьей – вычисляем значения функций. Используем инструмент «вставка – точечная» для построения графиков.
и построим графики левой и правой частей в Excel, изменяя х от -2 до 2 с шагом 0,5. В первой строке вводим значения переменной, во второй и третьей – вычисляем значения функций. Используем инструмент «вставка – точечная» для построения графиков.
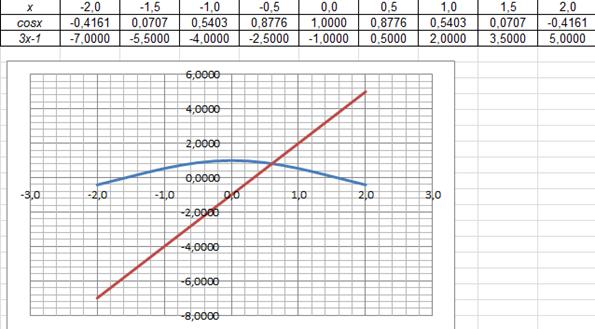
Рис. 2
Уточним корень на отрезке [0;1]. Определим начальную точку 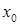 . В нашем случае
. В нашем случае 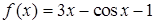 , тогда
, тогда 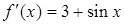 ,
, 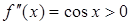 на исследуемом отрезке. Так как
на исследуемом отрезке. Так как 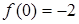 ,
, 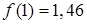 , то
, то 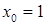 , в ней совпадают знаки функции и второй производной.
, в ней совпадают знаки функции и второй производной.
Метод хорд. В этом случае 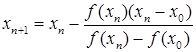 , составим вспомогательную таблицу
, составим вспомогательную таблицу
Таблица2
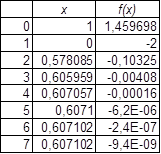
Так как |x5 – x4| = 0,0001 <0,001, то можно принять 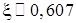 с точностью
с точностью 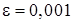 .
.
Метод касательных. Для этого метода справедливо 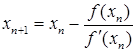 , начальная точка выбирается аналогично методу хорд, поэтому удобно воспользоваться следующей таблицей.
, начальная точка выбирается аналогично методу хорд, поэтому удобно воспользоваться следующей таблицей.
Таблица 3
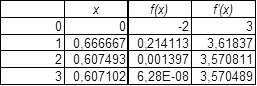
Так как |x3 – x2| = 0,0004 <0,001, то можно принять 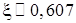 с точностью
с точностью 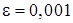 .
.
Метод Гаусса-Зейделя
Метод Гаусса-Зейделя представляет собой модификацию метода Якоби. Основная идея метода заключается в том, что при вычислении (k+1)-ой итерации неизвестное 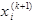 вычисляется с учетом уже найденных значений
вычисляется с учетом уже найденных значений
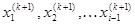 .
.
Проиллюстрируем метод для n=3. Пусть система линейных алгебраических уравнений уже приведена к нормальному виду:
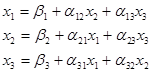
Выбираем произвольное начальное приближение 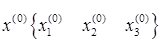 и подставляем в первое уравнение системы
и подставляем в первое уравнение системы
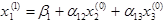
Полученное первое приближение 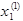 подставляем во второе уравнение системы (2.8)
подставляем во второе уравнение системы (2.8)
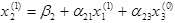
Используя 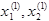 , находим
, находим 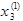 из третьего уравнения
из третьего уравнения
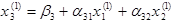
Этим заканчивается построение первой итерации
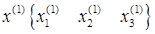
Используя значения первого приближения 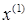 можно таким же способом построить следующие итерации. Итерацию с номером (k+1) можно представить следующим образом
можно таким же способом построить следующие итерации. Итерацию с номером (k+1) можно представить следующим образом
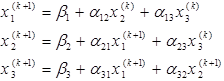
Итерационный процесс продолжается до тех пор, пока два соседних приближения 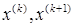 не станут достаточно близкими. Критерий близости может быть задан так же, как и в методе Якоби.
не станут достаточно близкими. Критерий близости может быть задан так же, как и в методе Якоби.
Метод Гаусса-Зейделя.
1. Заготовим таблицу на новом листе Excel как показано на рис.2.4.
2.
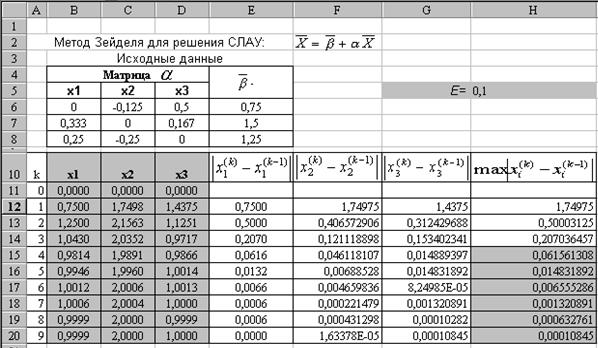 |
В качестве нулевого приближения выберем нулевой вектор
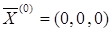 и введем его в ячейки В11: D 11.
и введем его в ячейки В11: D 11.
Рис.8
3. В ячейках В12: D 12 запишем формулы для вычисления первого приближения, используя (2.9). Эти формулы имеют вид:
B12=$E$6 + B11*$B$6 + C11*$C$6 + D11*$D$6,
C12==$E$7 + B12*$B$7 + C11*$C$7 + D11*$D$7,
D12==$E$8 + B12*$B$8 + C12*$C$8 + D11*$D$8.
4. В столбце Н сформируем вычисление M(k) , используя выражение, так, как это проделали в предыдущем примере
Анализируя результаты, принимаем 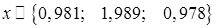 за приближенное решение исходной системы с заданной точностью.
за приближенное решение исходной системы с заданной точностью.
Основы численных методов
Методическое пособие для студентов
заочной формы обучения по направлению
«Информатика и вычислительная техника»
Березники, 2018
Составитель: старший преподаватель Н.Я. Захарова.
Основы численных методов. Методическое пособие для студентов заочной формы обучения по направлению «Информатика и вычислительная техника»/ Сост. Н.Я.Захарова; Перм. нац. исслед. политехн. ун–т. – Березники, 2018. – 25 с.
В пособии рассмотрено решение типовых заданий. Предложено 20 вариантов для контрольной работы.
© Пермский национальный
исследовательский
политехнический университет, 2018
Список литератур ы
1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Наука, 2006.
2. Березин И.С., Жидков Н.П. Методы вычислений. Т.1. – М.: Физматгиз, 1962.
3. Вержбицкий В.М. Основы численных методов. – М.: Высшая школа, 2001.
4. Воробьева Г.Н., Данилова А.Н. Практикум по вычислительной математике. – М.: Высшая Школа, 1990.
5. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах в 2-х ч. – М.: Высшая школа, 1999.
6. Демидович Б.П., Марон И.А. Основы вычислительной математики. – М.: Наука, 1970.
7. Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математике. – М.: Высшая школа, 1994.
8. Турчак Л.И. Основы численных методов. – М.: Наука, 1987.
Тема1. Решение уравнений
Задание 1. Отделить корни графически и уточнить любой корень с точностью до 0,001 методом деления пополам.
№ 1. 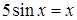 ; (кроме х=0) № 2.
; (кроме х=0) № 2. 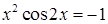 ;
;
№ 3. 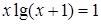 ; № 4.
; № 4. 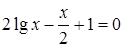 ;
;
№ 5. 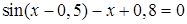 ; № 6.
; № 6. 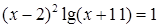 ;
;
№ 7. 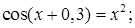 № 8.
№ 8. 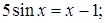
№ 9.  (кроме х=0) № 10.
(кроме х=0) № 10. 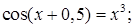
№ 11. 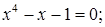 № 12.
№ 12. 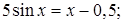
№ 13. 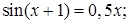 № 14.
№ 14. 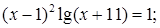
№ 15. 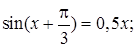 № 16.
№ 16. 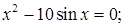 (кроме х=0)
(кроме х=0)
№ 17. 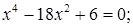 № 18.
№ 18. 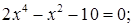
№ 19. 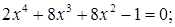 № 20.
№ 20. 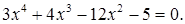
Образец выполнения задания. Найти один корень 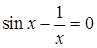 .
.
Перепишем уравнение в виде 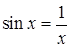 и построим графики левой и правой частей в Excel, изменяя х от 0,5 до 3 с шагом 0,5. В первой строке вводим значения переменной, во второй и третьей – вычисляем значения функций. Используем инструмент «вставка – точечная» для построения графиков.
и построим графики левой и правой частей в Excel, изменяя х от 0,5 до 3 с шагом 0,5. В первой строке вводим значения переменной, во второй и третьей – вычисляем значения функций. Используем инструмент «вставка – точечная» для построения графиков.

Рис. 1
Уточним корень на отрезке [1;2]. Для этого составим таблицу:
Таблица1
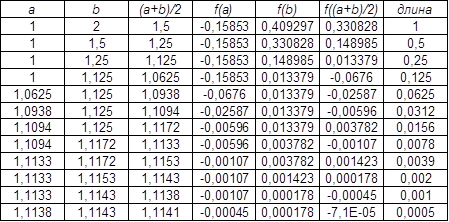
Длина последнего отрезка меньше 0,001, поэтому корень приближенно равен его середине, то есть 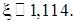
Задание 2. Отделить корни графически и уточнить с точностью до 0,001 больший корень обоих уравнений методами хорд и Ньютона.
№ 1. 1) 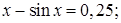 2)
2) 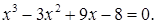
№ 2. 1) 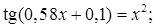 2)
2) 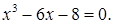
№ 3. 1) 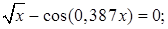 2)
2) 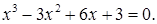
№ 4. 1) 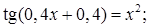 2)
2) 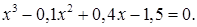
№ 5. 1) 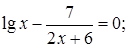 2)
2) 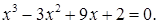
№ 6. 1) 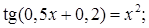 2)
2) 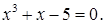
№ 7. 1) 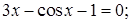 2)
2) 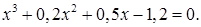
№ 8. 1) 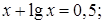 2)
2) 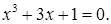
№ 9. 1) 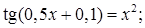 2)
2) 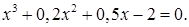
№ 10. 1) 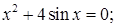 2)
2) 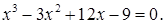
№ 11. 1) 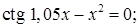 2)
2) 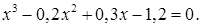
№ 12. 1) 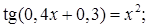 2)
2) 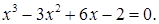
№ 13. 1) 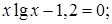 2)
2) 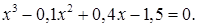
№ 14. 1) 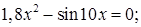 2)
2) 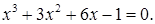
№ 15. 1) 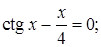 2)
2) 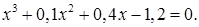
№ 16. 1) 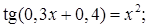 2)
2) 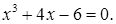
№ 17. 1)  2)
2) 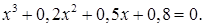
№ 18. 1) 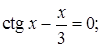 2)
2) 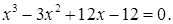
№ 19. 1) 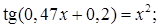 2)
2) 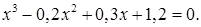
№ 20. 1) 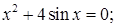 2)
2) 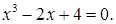
Образец выполнения задания. Найти один корень 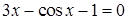 .
.
Перепишем уравнение в виде 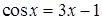 и построим графики левой и правой частей в Excel, изменяя х от -2 до 2 с шагом 0,5. В первой строке вводим значения переменной, во второй и третьей – вычисляем значения функций. Используем инструмент «вставка – точечная» для построения графиков.
и построим графики левой и правой частей в Excel, изменяя х от -2 до 2 с шагом 0,5. В первой строке вводим значения переменной, во второй и третьей – вычисляем значения функций. Используем инструмент «вставка – точечная» для построения графиков.

Рис. 2
Уточним корень на отрезке [0;1]. Определим начальную точку 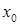 . В нашем случае
. В нашем случае 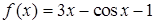 , тогда
, тогда 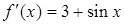 ,
, 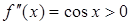 на исследуемом отрезке. Так как
на исследуемом отрезке. Так как 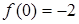 ,
, 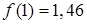 , то
, то 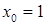 , в ней совпадают знаки функции и второй производной.
, в ней совпадают знаки функции и второй производной.
Метод хорд. В этом случае 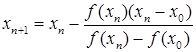 , составим вспомогательную таблицу
, составим вспомогательную таблицу
Таблица2
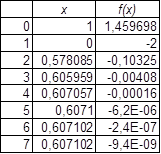
Так как |x5 – x4| = 0,0001 <0,001, то можно принять 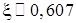 с точностью
с точностью 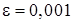 .
.
Метод касательных. Для этого метода справедливо 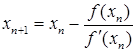 , начальная точка выбирается аналогично методу хорд, поэтому удобно воспользоваться следующей таблицей.
, начальная точка выбирается аналогично методу хорд, поэтому удобно воспользоваться следующей таблицей.
Таблица 3
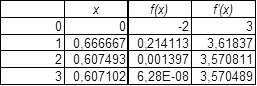
Так как |x3 – x2| = 0,0004 <0,001, то можно принять 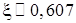 с точностью
с точностью 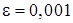 .
.
Дата: 2019-02-25, просмотров: 430.