Тема 2. Численные методы решения задач линейной алгебры,

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

метод Гаусса

Решить систему линейных алгебраических уравнений (СЛАУ) 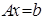, вычислить определитель и обратную матрицу для матрицы А методом исключения Гаусса, используя схему Халецкого.

1). 3,5x₁ - 1,7x₂ + 2,8x₃ = 1,7, 5,7x₁ + 3,3x₂ + 1,3x₃ = 2,1, 2,1x₁ + 5,8x₂ + 2,8x₃ = 0,8.	2). 2,1x₁ + 4,4x₂ + 1,8x₃ = 1,1, 0,7x₁ - 2,8x₂ + 3,9x₃ = 0,7, 4,2x₁ - 1,7x₂ + 1,3x₃ = 2,8.
3). 3,1x₁ + 2,8x₂ + 1,9x₃ = 0, 1,9x₁ + 3,1x₂ + 2,1x₃ = 2,1, 7,5x₁ + 3,8x₂ + 4,8x₃ = 5,6.	4). 4,1x₁ + 5,7x₂ + 1,2x₃ = 5,8, 0,8x₁ + 1,1x₂ - 2,8x₃ = 6,7, 9,1x₁ - 3,6x₂ + 2,8x₃ = 9,8.
5). 2,7x₁ - 0,8x₂ + 4,1x₃ = 3,2, 1,1x₁ + 3,7x₂ + 1,8x₃ = 5,7, 3,3x₁ + 2,1x₂ - 2,8x₃ = 0,8.	6). 1,9x₁ + 1,1x₂ + 3,8x₃ = 7,8, 7,6x₁ + 5,8x₂ - 4,7x₃ = 10,1, 1,8x₁ - 4,1x₂ + 2,1x₃ = 9,7.
7). 3,2x₁ - 8,5x₂ + 3,7x₃ = 6,5, 0,5x₁ + 0,34x₂ +3,7x₃ = -0,24, 4,6x₁ + 2,3x₂ - 1,5x₃ = 4,3.	8). 4,2x₁ + 6,7x₂ - 2,3x₃ = 2,7, 5,4x₁ - 2,3x₂ + 1,4x₃ = - 3,5, 3,4x₁ + 2,4x₂ + 7,4x₃ = 1,9.
9). 1,5x₁ + 4,5x₂ + 1,3x₃ = -1,7, 2,7x₁ - 3,6x₂ + 6,9x₃ = 0,4, 6,6x₁ + 1,8x₂ - 4,7x₃ = 3,8.	10). 3,4x₁ - 3,6x₂ - 7,7x₃ = -2,4, 5,6x₁ + 2,7x₂ - 1,7x₃ = 1,9, -3,8x₁ + 1,3x₂ +3,7x₃ = 1,2.
11). -2,7x₁ + 0,9x₂ - 1,5x₃ = 3,5, 3,5x₁ - 1,8x₂ + 6,7x₃ = 2,6, 5,1x₁ + 2,7x₂ + 1,4x₃ = -0,1.	12). 0,8x₁ + 7,4x₂ - 0,5x₃ = 6,4. 3,1x₁ - 0,6x₂ - 5,3x₃ = -1,5, 4,5x₁ - 2,5x₂ + 1,4x₃ = 2,5.
13). 5,4x₁ - 6,2x₂ - 0,5x₃ = 0,52, 3,4x₁ + 2,3x₂ + 0,8x₃ = -0,8, 2,4x₁ - 1,1x₂ + 3,8x₃ = 1,8.	14). 3,8x₁ + 6,7x₂ + 2,2x₃ = 5,2, 6,4x₁ + 1,3x₂ - 2,7x₃ = 3,8, -2,4x₁ - 4,5x₂ + 3,5x₃ = -0,6.
15). -3,3x₁ + 1,1x₂ + 5,8x₃ = 2,3, 7,8x₁ + 5,3x₂ + 1,8x₃ = 1,8, 4,5x₁ + 3,3x₂ - 3,8x₃ = 3,4.	16). 3,8x₁ + 7,1x₂ - 2,3x₃ = 4,8, -2,1x₁ + 3,9x₂ - 6,8x₃ = 3,3, 8,8x₁ + 1,1x₂ - 2,1x₃ = 5,8.
17). 1,7x₁ - 2,2x₂ - 4,0x₃ = 1,8, 2,1x₁ + 1,9x₂ - 2,3x₃ = 2,8, 4,2x₁ + 1,9x₂ - 0,1x₃ = 5,1.	18). 2,8x₁ + 3,8x₂ – 8,2x₃ = 4,5, 2,5x₁ - 7,8x₂ + 3,3x₃ = 7,1, 6,5x₁ - 1,1x₂ + 4,8x₃ = 6,3.
19). 2,3x₁ + 0,7x₂ + 4,2x₃ = 5,8, -2,7x₁ + 2,3x₂ - 2,9x₃ = 6,1, 9,1x₁ + 4,8x₂ - 5,0x₃ = 7,0.	20) . 3,1x₁ + 6,8x₂ + 2,1x₃ = 7,0, -5,0x₁ - 4,8x₂ + 5,3x₃ = 6,1, 8,2x₁ + 1,8x₂ + 5,1x₃ = 5,8.

Итерационные методы решения систем линейных алгебраических уравнений

1. Решить СЛАУ методами Якоби и Гаусса–Зейделя с заданной точностью: e=0,01. Проанализировать результаты решения (в зависимости от других значений e.)

2. Сравнить результаты решения, полученные двумя методами, сделать соответствующие выводы.

Для расчета использовать СЛАУ 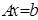, заданную в соответствием с вариантом.

1). 3,5х₁ - 1,7х₂ + 2,8х₃ = 1,7 5,7х₁ + 3,3х₂ + 1,3х₃ = 2,1 2,1х₁ + 5,8х₂ + 2,8х₃ = 0,8	2). 2,1х₁ + 4,4х₂ + 1,8х₃ = 1,1 0,7х₁ - 2,8х₂ + 3,9х₃ = 0,7 4,2х₁ - 1,7х₂ + 1,3х₃ = 2,8
3). 3,1х₁ + 2,8х₂ + 1,9х₃ = 0, 1,9х₁ + 3,1х₂ + 2,1х₃ = 2,1 7,5х₁ + 3,8х₂ + 4,8х₃ = 5,6	4). 4,1х₁ + 5,7х₂ + 1,2х₃ = 5,8 0,8х₁ + 1,1х₂ - 2,8х₃ = 6,7 9,1х₁ - 3,6х₂ + 2,8х₃ = 9,8
5). 2,7х₁ - 0,8х₂ + 4,1х₃ = 3,2 1,1х₁ + 3,7х₂ + 1,8х₃ = 5,7 3,3х₁ + 2,1х₂ - 2,8х₃ = 0,8	6). 1,9х₁ + 1,1х₂ + 3,8х₃ = 7,8 7,6х₁ + 5,8х₂ - 4,7х₃ = 10,1 1,8х₁ - 4,1х₂ + 2,1х₃ = 9,7
7) 3,2х₁ - 8,5х₂ + 3,7х₃ = 6,5 0,5х₁ + 0,34х₂ +3,7х₃ = -0,24 4,6х₁ + 2,3х₂ - 1,5х₃ = 4,3.	8). 4,2х₁ + 6,7х₂ - 2,3х₃ = 2,7; 5,4х₁ - 2,3х₂ + 1,4х₃ = - 3,5; 3,4х₁ + 2,4х₂ + 7,4х₃ = 1,9.
9). 1,5х₁ + 4,5х₂ + 1,3х₃ = -1,7 2,7х₁ - 3,6х₂ + 6,9х₃ = 0,4 6,6х₁ + 1,8х₂ - 4,7х₃ = 3,8	10). 3,4х₁ - 3,6х₂ - 7,7х₃ = -2,4 5,6х₁ + 2,7х₂ - 1,7х₃ = 1,9 -3,8х₁ + 1,3х₂ +3,7х₃ = 1,2
11). -2,7х₁ + 0,9х₂ - 1,5х₃ = 3,5 3,5х₁ - 1,8х₂ + 6,7х₃ = 2,6 5,1х₁ + 2,7х₂ + 1,4х₃ = -0,1	12). 0,8х₁ + 7,4х₂ - 0,5х₃ = 6,4. 3,1х₁ - 0,6х₂ - 5,3х₃ = -1,5; 4,5х₁ - 2,5х₂ + 1,4х₃ = 2,5.
13). 5,4х₁ - 6,2х₂ - 0,5х₃ = 0,52 3,4х₁ + 2,3х₂ + 0,8х₃ = -0,8 2,4х₁ - 1,1х₂ + 3,8х₃ = 1,8	14). 3,8х₁ + 6,7х₂ + 2,2х₃ = 5,2 6,4х₁ + 1,3х₂ - 2,7х₃ = 3,8 -2,4х₁ - 4,5х₂ + 3,5х₃ = -0,6
15). -3,3х₁ + 1,1х₂ + 5,8х₃ = 2,3 7,8х₁ + 5,3х₂ + 1,8х₃ = 1,8 4,5х₁ + 3,3х₂ - 3,8х₃ = 3,4	16). 3,8х₁ + 7,1х₂ - 2,3х₃ = 4,8 -2,1х₁ + 3,9х₂ - 6,8х₃ = 3,3 8,8х₁ + 1,1х₂ - 2,1х₃ = 5,8
17). 1,7х₁ - 2,2х₂ - 4,0х₃ = 1,8 2,1х₁ + 1,9х₂ - 2,3х₃ = 2,8 4,2х₁ + 1,9х₂ - 0,1х₃ = 5,1	18). 2,8х₁ + 3,8х₂ – 8,2х₃ = 4,5 2,5х₁ - 7,8х₂ + 3,3х₃ = 7,1 6,5х₁ - 1,1х₂ + 4,8х₃ = 6,3
19). 2,3х₁ + 0,7х₂ + 4,2х₃ = 5,8 -2,7х₁ + 2,3х₂ - 2,9х₃ = 6,1 9,1х₁ + 4,8х₂ - 5,0х₃ = 7,0	20). 3,1х₁ + 6,8х₂ + 2,1х₃ = 7,0 -5,0х₁ - 4,8х₂ + 5,3х₃ = 6,1 8,2х₁ + 1,8х₂ + 5,1х₃ = 5,8

Указания к выполнению работы

1. Привести систему к виду, когда матрица имеет диагональное преобладание.

2. Привести полученную систему к нормальному виду .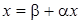

3. Решить систему методами Якоби и Гаусса–Зейделя, используя приложение Excel.

4. Проследить сходимость итерационного процесса, построив графики изменения каждой компоненты решения в зависимости от номера итерации (см. рис.7).

Метод Якоби (метод простых итераций)

Задана система линейных алгебраических уравнений

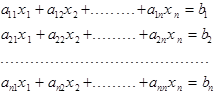Или в матричной форме 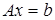. Полагая, что диагональные коэффициенты

a_ii ¹ 0 (i = 1, 2, … n) ,

разрешим первое уравнение системы относительно х₁, второе – относительно х₂ и т.д. Тогда получим эквивалентную систему

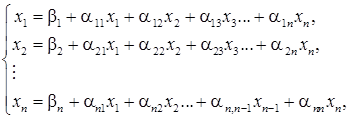
где 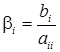, 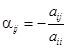и 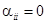(i, j = 1, 2, … n).

Введя матрицы 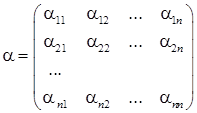и 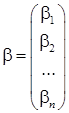, исходную систему можно записать в матричной форме

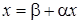а любое (k + 1) приближение вычисляется по формуле

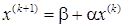За начальное приближение решения можно взять столбец свободных членов 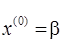т.е.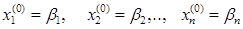

Строим последовательность приближений (итераций)

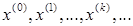Если эта последовательность имеет предел 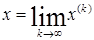, то он является точным решением системы. На практике итерационный процесс продолжается до тех пор, пока два соседних приближения не станут достаточно близкими.

Критерий близости двух приближений может быть определен следующим образом:

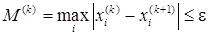
Если условие выполнено, то итерационный процесс прекращается и за приближенное решение системы с заданной точностью e принимается последнее найденное приближение, т.е.

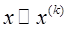Метод Гаусса-Зейделя

Метод Гаусса-Зейделя представляет собой модификацию метода Якоби. Основная идея метода заключается в том, что при вычислении (k+1)-ой итерации неизвестное 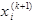вычисляется с учетом уже найденных значений

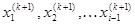Проиллюстрируем метод для n=3. Пусть система линейных алгебраических уравнений уже приведена к нормальному виду:

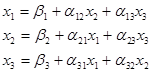
Выбираем произвольное начальное приближение 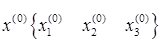и подставляем в первое уравнение системы

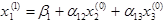
Полученное первое приближение 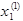подставляем во второе уравнение системы (2.8)

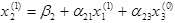
Используя 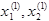, находим 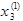из третьего уравнения

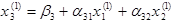
Этим заканчивается построение первой итерации

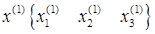
Используя значения первого приближения 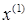можно таким же способом построить следующие итерации. Итерацию с номером (k+1) можно представить следующим образом

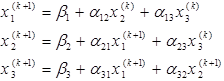
Итерационный процесс продолжается до тех пор, пока два соседних приближения 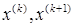не станут достаточно близкими. Критерий близости может быть задан так же, как и в методе Якоби.

Дата: 2019-02-25, просмотров: 252.

⇐ Предыдущая 123 Следующая ⇒