Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, определяющими их величину.

Моделирование – это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность его заключается в том, что взаи­мосвязь исследуемого показателя с факторными передается в форме конкретного математического выражения.

В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помо­щью детерминированных факторных моделей исследуется функ­циональная связь между результативным показателем (функцией) и факторами (аргументами).

При создании детерминированных факторных моделей необ­ходимо выполнять ряд требований:

1) факторы, включаемые в модель, должны реально существовать, а не быть надуманными абстрактными величинами или яв­лениями;

2) факторы, входящие в модель, должны находиться в причин­но-следственной связи с изучаемым показателем;

3) все показатели факторной модели должны быть количе­ственно измеримыми, т.е. иметь единицу измерения и необходи­мую информационную базу;

4) факторная модель должна обеспечивать возможность изме­рения влияния отдельных факторов, т.е. в ней должна учитываться соразмерность изменений результативного и факторных показате­лей, а сумма влияния отдельных факторов должна равняться об­щему приросту результативного показателя.

В детерминированном анализе выделяют следующие типы наи­более часто встречающихся факторных моделей.

1. Аддитивные модели: 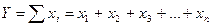, например, выпуск продукции по подразделениям.

2. Мультипликативные модели: 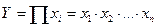, например, среднегодовая выработка одного работника.

3. Кратные модели: 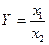, например, фондоотдача.

4. Смешанные (комбинированные) модели - сочетание в различ­ных комбинациях предыдущих моделей, например, рентабельность производственных фондов.

Моделирование мультипликативных факторных систем в АХД осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Например, при ис­следовании процесса формирования объема производства продук­ции можно применять следующие детерминирован­ные модели:

ВП = ЧР · ГВ;         ВП = ЧР · Д · ДВ;         ВП = ЧР · Д · П · ЧВ

Эти модели отражают процесс детализации исходной фактор­ной системы мультипликативного вида и расширения ее за счет расчленения на сомножители факторов. Степень де­тализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил.

Аналогичным образом, т.е. путем расчленения одного из фак­торных показателей на составные элементы, осуществляется мо­делирование аддитивных факторных систем.

Как известно, объем реализации продукции равен

РП = ВП – О_н.п.,

где ВП - объем выпуска продукции;

О_н.п - остатки нереализованной продукции.

Часть нереализованной продукции может находиться на складах предприятия (О_скл), а часть может быть отгружена покупателям, но еще не оплачена (О_отг). Тогда приведенную исходную модель мож­но записать следующим образом:

РП = ВП – О_скл – О_отг.

К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расшире­ния и сокращения.

Метод удлинения предусматривает удлинение числителя исход­ной модели путем замены одного или нескольких факторов на сум­му однородных показателей. Например, себестоимость единицы продукции можно представить в качестве функции двух факторов: изменения суммы затрат (3) и объема выпуска продукции (ВП). Исходная модель этой факторной системы будет иметь следующий вид: С =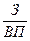

Если общую сумму затрат (3) заменить отдельными их элемен­тами, такими, как заработная плата (ЗП), материальные затраты (МЗ), амортизация основных средств (А), накладные расходы ( HP ) и др., то детерминированная факторная модель будет иметь вид аддитивной модели с новым набором факторов: С = 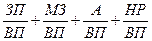= х₁ +х₂ + х₃ + х₄

где х₁ - трудоемкость продукции;

х₂ - материалоемкость продукции;

х₃ - фондоемкость продукции;

х₄ - уровень накладных расходов.

Способ формального разложения факторной системы предусмат­ривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведе­ние однородных показателей. Если b = l + т + п + р, то Y = а/ b =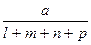  

В результате получили конечную модель кратно-аддитивного вида с новым набором факторов. Например, при анализе показателя рентабельности производства (R):  R = П/З · 100,

где П - сумма прибыли от реализации продукции;

3 - сумма затрат на производство и реализацию продукции.

Если сумму затрат заменить на отдельные ее элементы, конеч­ная модель в результате преобразования приобретет следующий вид: R =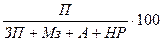

Метод расширения предусматривает расширение исходной факторной модели путем умножения числителя и знаменателя дроби на один или несколько новых показателей. Например, если в ис­ходную модель Y = 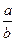   ввести новый показатель с, то модель примет следующий вид:

Y = 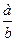 =  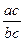=  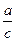·  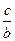= х₁ · х₂

В результате получается конечная мультипликативная модель в виде произведения нового набора факторов.

Этот способ моделирования очень широко применяется в ана­лизе. Например, среднегодовую выработку продукции одним ра­ботником (показатель производительности труда) можно записать таким образом: ГВ = ВП/ЧР

Если ввести такой показатель, как количество отработанных дней всеми работниками (Д_общ), то получим следующую модель го­довой выработки:

ГВ = 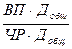 =  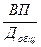·  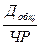= ДВ · Д

где ДВ - среднедневная выработка;

Д - количество отработанных дней одним работником.

Метод сокращения представляет собой создание новой фактор­ной модели путем деления числителя и знаменателя дроби на один и тот же показатель: Y = а/ b =  =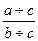

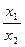
В данном случае получается конечная модель того же типа, что и исходная, однако с другим набором факторов.

Например, рентабельность операционного капитала рассчиты­вается делением суммы прибыли от реализации продукции (П) на среднегодовую стоимость основного и оборотного капитала пред­приятия (KL): R = П/ KL

Если числитель и знаменатель разделить на выручку от реали­зации продукции (В), то получим кратную модель, но с новым на­бором факторов - рентабельности продаж и капиталоемкости продукции: R = = =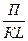

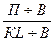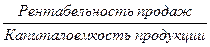
Для преобразования од­ной и той же модели может быть последовательно использовано несколько методов.

Процесс моделирования факторных систем - очень сложный и ответственный момент в АХД. От того, насколько реально и точ­но созданные модели отражают связь между исследуемыми пока­зателями, зависят конечные результаты анализа.