Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

    Числа оборотов валов и угловые скорости:

n₁ = n_дв = 920 об/мин w₁ = 920π/30 = 96,3 рад/с

n₂ = n₁/u₁ = 920/40  = 23 об/мин w₂= 23π/30 = 2,41 рад/с

n₃ = n₂/u₂ = 23/6,05 = 3,8 об/мин w₃= 3,8π/30 = 0,40 рад/с

            Фактическое значение скорости вращения колонны

v = πDn₃/6·10⁴ = π350·3,8/6·10⁴ = 0,07 м/с

            Отклонение фактического значения от заданного

δ = 0 < 4%

    Мощности передаваемые валами:

P₁ = P_трη_мη_пк = 1050·0,98·0,995 = 1023 Вт

P₂ = P₁η_зпη_пк = 1023·0,72·0,995 = 733 Вт

P₃ = P₂η_опη_пс = 733·0,94·0,99 = 682 Вт

    Крутящие моменты:

Т₁ = P₁/w₁ = 1023/96,3 = 10,6 Н·м

Т₂ = 733/2,41 =304,1 Н·м

Т₃ = 682/0,40 = 1700 Н·м

     Результаты расчетов сводим в таблицу

Вал	Число оборо­тов об/мин	Угловая ско­рость Рад/сек	Мощность кВт	Крутящий момент Н·м
Вал электродвигателя	920	96,3	1,050	10,9
Ведущий редуктора	920	96,3	1,023	10,6
Ведомый редуктора	23	2,41	0,733	304,1
Рабочий привода	3.8	0,40	0,682	1700,0

 

3 Выбор материалов червячной передач и определение допускаемых напряжений

Принимаем, согласно рекомендациям [1c.53],  для червяка сталь 45 улучшенная до твердости  не выше HВ350.

    Ориентировочное значение скорости скольжения:

v_s = 4,2uw₂10^-3M₂^1/3 = 4,2×40,0×2,41×10^-3×304,1^1/3 = 2,72 м/с,

при v_s <5 м/с рекомендуется [1 c54] бронза БрА10Ж4Н4, способ отливки – центробежный: s_в = 700 МПа, s_т = 460 МПа.

 

Допускаемые контактные напряжения:

[s]_H = 250 – 25v_s = 250 – 25×2,72 = 182 МПа.

Допускаемые напряжения изгиба при реверсивной передаче:

[s]_F = 0,16s_вK_FL,

где К_FL – коэффициент долговечности.

K_FL = (10⁶/N_эН)^1/9,

где N_эН – число циклов перемены напряжений.

N_эН = 573w₂L_h = 573×2,41×30000 = 4,1×10⁷.

    K_FL = (10⁶/4,1×10⁷)^1/9 = 0,662

[s]_F = 0,16×700×0,662 = 74 МПа.

Таблица 3.1

Механические характеристики материалов червячной передачи

Элемент передачи	Марка стали	Термоо-бработка	σв	σ-1	[σ]Н	[σ]F
			Н/мм2
Червяк	45	Улучшен. < 350HB	780	335
Колесо	Сборное				182	74

 

 

4 Расчет закрытой червячной передачи

Межосевое расстояние

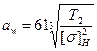 = 61(304,1×10³/182²)^1/3 =128 мм

принимаем а_w = 125 мм

Основные геометрические параметры передачи

Модуль зацепления:

m = (1,5¸1,7)a_w/z₂,

где z₂ – число зубьев колеса.

При передаточном числе 40,0 число заходов червяка z₁ = 1, тогда число зубьев колеса:

z₂ = z₁u = 1×40,0 = 40,0

m = (1,5¸1,7)125/40 = 4,7¸5,3 мм,

принимаем m = 5,0 мм.

Коэффициент диаметра червяка:

q = (0,212¸0,25)z₂ = (0,212¸0,25)40 = 8,5¸10

принимаем q = 10

Коэффициент смещения

x = a/m – 0,5(q+z₂) = 125/5,0 – 0,5(10+40) = 0

Фактическое значение межосевого расстояния:

a_w = 0,5m(q+z₂+2x) = 0,5×5,0(10+40 – 2×0) = 125 мм

Делительный диаметр червяка:

d₁ = qm =10×5,0 = 50,0 мм

Начальный диаметр червяка d_w1 = m(q+2x) = 5,0(10-2·0) = 50,0 мм

Диаметр вершин витков червяка:

d_a1 = d₁+2m = 50,0+2×5,0 = 60 мм.

Диаметр впадин витков червяка:

d_f1 = d₁ – 2,4m = 50,0 – 2,4×5,0 = 38,0 мм.

 

 

Длина нарезной части червяка:

b₁ = (10+5,5|x|+z₁)m + C = (10+5,5×0+2)5,0+0 = 60 мм.

при х < 0 ® С = 0.

Делительный угол подъема линии витка:

g = arctg(z₁/q) = arctg(1/10) = 5,71°

Делительный диаметр колеса:

d₂ = mz₂ = 5,0×40 = 200,0 мм.

Диаметр выступов зубьев колеса:

d_a2 = d₂+2m(1+x) = 200,0+2×5,0(1-0) = 210,0 мм.

Диаметр впадин зубьев колеса:

d_f2 = d₂ – 2m(1,2 – x) = 200,0 – 2×5,0(1,2 + 0) = 188,0 мм.

Наибольший диаметр зубьев колеса:

d_am2 = d_a2+6m/(z₁+2) = 210,0+6×5,0/(1+2) = 220,0 мм.

Ширина венца колеса:

b₂ = 0,355a_w = 0,355×125 = 44 мм.

2.5. Фактическое значение скорости скольжения

v_s = uw₂d₁/(2000cosg) = 40,0∙2,41×50,0/(2000cos 5,71°) = 2,42 м/с

    Уточняем значение допускаемого контактного напряжения

[s]_H = 250 – 25v_s = 250 – 25×2,42 = 190 МПа.

2.6. Коэффициент полезного действия червячной передачи

h = (0,95¸0,96)tgg/tg(g+j)

где j = 2,0º - приведенный угол трения [1c.74].

h = (0,95¸0,96)tg 5,71°/tg( 5,71°+2,0º) = 0,71.

2.7. Силы действующие в зацеплении

       Окружная на колесе и осевая на червяке:

F_t2 = F_a1 = 2Т₂/d₂ = 2×304,1×10³/200,0 = 3041 H.

    Радиальная на червяке и колесе:

F_r1 = F_r2 = F_t2tga = 3041×tg20° =1107 H.

 

 

    Окружная на червяке и осевая на колесе:

F_t1 = F_a2 = 2M₁/d₁ = 2×10,6×10³/50,0 = 424 H.

2.8. Расчетное контактное напряжение

s_Н = 340(F_t2K/d₁d₂)^0,5,

    где К – коэффициент нагрузки.

    Окружная скорость колеса

v₂ = w₂d₂/2000 = 2,41×200,0/2000 = 0,24 м/с

    при v₂ < 3 м/с ® К = 1,0

s_Н = 340(3041×1,0/50,0×200,0)^0,5 = 187 МПа,

перегрузка (187 – 182)100/182,0 = 2,7% < 5%.

Расчетное напряжение изгиба для зубьев колеса

s_F = 0,7Y_F2F_t2K/(b₂m),

где Y_F2 – коэффициент формы зуба колеса.

Эквивалентное число зубьев колеса:

z_v2 = z₂/(cosg)³ = 40/(cos 5,71°)³ = 40,6 ® Y_F2 = 1,54.

s_F = 0,7×1,54×3031×1,0/(44×5,0) = 14,9 МПа.

Условие s_F < [s]_F = 74 МПа выполняется.

 

Так как условия  0,85<s_H < 1,05[s_H] и s_F < [s_F]  выполняются, то можно утверждать, что устойчивая работа червячной закрытой пере­дачи обеспечена в течении всего срока службы привода.

 

5 Расчет открытой зубчатой передачи

Выбор материалов зубчатой передачи

Принимаем, согласно рекомендациям [1c.52], сталь 45:

шестерня: термообработка – улучшение – НВ235÷262 [1c.53],

колесо: термообработка – нормализация – НВ179÷207.

Средняя твердость зубьев:

НВ_1ср = (235+262)/2 = 248

НВ_2ср = (179+207)/2 = 193

Допускаемые контактные напряжения:

[σ]_H = K_HL[σ]_H0,

где K_HL – коэффициент долговечности

K_HL = (N_H0/N)^1/6,

где N_H0 = 1·10⁷ [1c.55],

N = 573ωL_h  = 573·0,40·30,0·10³ = 6,88·10⁷.

Так как N > N_H0, то К_HL = 1.

[σ]_H2 = 1,8HB+67 = 1,8·193+67 = 414 МПа.

 

Допускаемые напряжения изгиба:

[σ]_F = K_FL[σ]_F0,

где K_FL – коэффициент долговечности

Так как N > N_F0 = 4·10⁶, то К_FL = 1.

[σ]_F01 = 1,03HB₁ = 1,03·248 = 255 МПа.

 [σ]_F02 = 1,03HB₂ = 1,03·193 = 199 МПа.

[σ]_F1 = 1·255 = 255 МПа.

[σ]_F2 = 1·199 = 199 МПа.

 

 

Межосевое расстояние

    ,

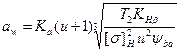где К_а = 49,5 – для прямозубых передач [1c.58],

      ψ_ba = 0,20 – коэффициент ширины колеса,

      К_Нβ = 1,0 – для прирабатывающихся колес.

а_w = 49,5(6,05+1)[1700·10³·1,0/(414²·6,05²·0,20)]^1/3 = 386 мм

принимаем согласно ГОСТ 2185-66 [2 c.52] а_w = 380 мм.

Модуль зацепления

m > 2K_mT₂/(d₂b₂[σ]_F),

    где K_m = 6,8 – для прямозубых колес,

  d₄ – делительный диаметр колеса,

d₄ = 2a_wu/(u+1) = 2·380·6,05/(6,05+1) = 652 мм,

   b₄ – ширина колеса

b₄ = ψ_baa_w = 0,20·380 = 76 мм.

m > 2·6,8·1700·10³/652·76·199 = 2,34 мм,

в открытых передачах расчетное значение модуля увеличивают на 30%, поэтому принимаем по ГОСТ 9563-60 m = 4,0 мм.

Основные геометрические размеры передачи

    Суммарное число зубьев:

z_c = 2a_w/m = 2·380/4,0 = 190

Число зубьев шестерни:

z₃ = z_c/(u+1) = 190/(6,05+1) =27

Число зубьев колеса:

z₄ = z_c – z₃ = 190 – 27 =163

Фактическое передаточное число:

u = z₄/z₃ =163/27 = 6,04.

Фактическое межосевое расстояние:

a_w = (z₃+z₄)m/2 = (163+27)·4,0/2 = 380 мм.

 

       делительные диаметры

  d₃ = mz₁₃  = 4,0·27 =108 мм,       

d₄ = 4,0·163= 652 мм,

       диаметры выступов

d_a3 = d₃+2m =108+2·4,0 =116 мм            

d_a4 = 652+2·4,0 = 660 мм

       диаметры впадин

d_f3 = d₃ – 2,4m =108 – 2,5·4,0 = 98 мм

d_f4 = 652 – 2,5·4,0 = 642 мм

      ширина колеса b₄ = y_baa_w = 0,20·380 = 76 мм

ширина шестерни b₃ = b₄ + 5 = 76+5 = 81 мм

Окружная скорость

v = ω₂d₃/2000 = 2,41·108/2000 = 0,13 м/с

Принимаем 8-ую степень точности.

Силы действующие в зацеплении

- окружная 

F_t2 = 2T₂/d₃ = 2·304,1·10³/108 = 5631 H

- радиальная

F_r2 = F_t2tga = 5631tg20º =2050 H

Расчетное контактное напряжение

,

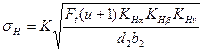где К = 436 – для прямозубых колес [1c.61],

  К_Нα = 1 – для прямозубых колес,

      К_Нβ = 1,0 – для прирабатывающихся зубьев,

      К_Нv = 1,02 – коэффициент динамической нагрузки [1c.62].

σ_H = 436[5631(6,04+1)1,0·1,0·1,02/(652·76)]^1/2 = 394 МПа.

недогрузка (414 – 394)100/414 = 4,9% допустимо 10%.

 

 

Расчетные напряжения изгиба

σ_F4 = Y_F4Y_βF_tK_FαK_FβK_Fv/(mb₂),

    где Y_F4 – коэффициент формы зуба,

  Y_β = 1 – для прямозубых колес,

      K_Fα = 1,0 – для прямозубых колес,

  K_Fβ = 1 – для прирабатывающихся зубьев

      K_Fv = 1,05 – коэффициент динамической нагрузки [1c.64].

Коэффициент формы зуба:

при z₃ = 27  → Y_F3 = 3,85,

при z₄ = 163 → Y_F4 = 3,61.

σ_F4 = 3,61·1,0·5631·1,0·1,0·1,05/4,0·76 = 70 МПа < [σ]_F4

σ_F3 = σ_F4Y_F3/Y_F4 = 70·3,85/3,61 = 75 МПа < [σ]_F3.

 

Так как условия  0,85<s_H < 1,05[s_H] и s_F < [s_F]  выполняются, то можно утверждать, что устойчивая работа зубчатой открытой пере­дачи обеспечена в течении всего срока службы привода.

 

6 Нагрузки валов редуктора

Силы действующие в зацеплении червячной передачи

       Окружная на колесе и осевая на червяке:

F_t2 = F_a1 = 3041 H.

    Радиальная на червяке и колесе:

F_r1 = F_r2 =1107 H.

    Окружная на червяке и осевая на колесе:

F_t1 = F_a2 = 424 H.

Консольная сила от муфты действующая на быстроходный вал

F_м = 100·Т₁^1/2 = 100·10,6^1/2 = 326 Н

Консольная силы действующие на тихоходный вал

Окружная 

F_t2 = 5631 H

Радиальная

F_r2 = 2050 H

 

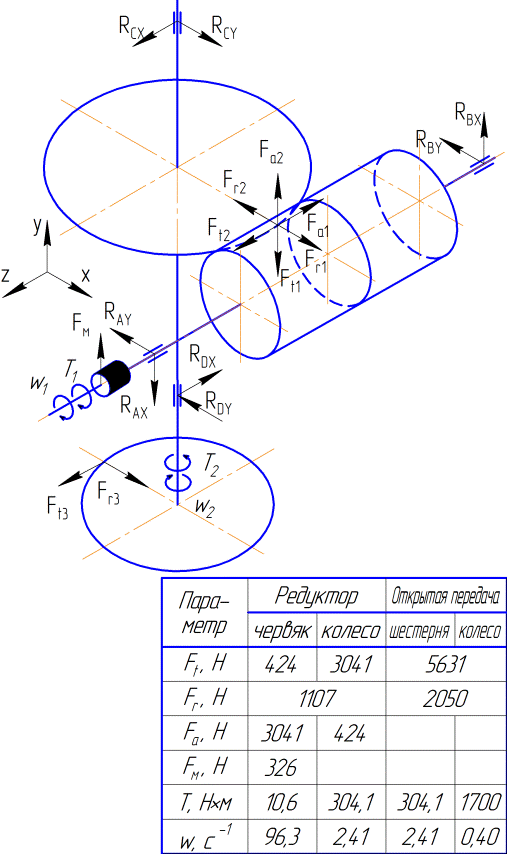
Рис. 6.1 – Схема нагружения валов червячного редуктора

 

7 Проектный расчет валов. Эскизная компоновка редуктора.

 

Материал быстроходного вала – сталь 45,

термообработка – улучшение: σ_в = 780 МПа; 

Допускаемое напряжение на кручение [τ]_к = 10÷25 МПа

  Диаметр быстроходного вала

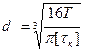
   где Т – передаваемый момент;

d₁ = (16∙10,6·10³/π10)^1/3 = 17 мм

Ведущий вал редуктора соединяется с помощью стандартной муфты с валом электродвигателя диаметром d_дв= 22 мм,

d₁ = (0,8¸1,2)d_дв = (0,8¸1,2)22 = 18¸26 мм

    принимаем диаметр выходного конца d₁ = 25 мм;

    длина выходного конца:

l₁ = (1,0¸1,5)d₁ = (1,0¸1,5)25 = 25¸38 мм,

   принимаем l₁ = 40 мм.

   Диаметр вала под уплотнением:

d₂ = d₁+2t = 25+2×2,2 = 29,4 мм,

   где t = 2,2 мм – высота буртика;

   принимаем d₂ = 30 мм:

   длина вала под уплотнением:

l₂ » 1,5d₂ =1,5×30 = 45 мм.

   Диаметр вала под подшипник:

d₄ = d₂ = 30 мм.

   Вал выполнен заодно с червяком

 

 

  Диаметр выходного конца тихоходного вала:

d₁ = (304,1·10³/π15)^1/3 = 47 мм

принимаем диаметр выходного конца d₁ = 50 мм;

Диаметр вала под уплотнением:

d₂ = d₁+2t = 50+2×2,8 = 56,6 мм,

где t = 2,8 мм – высота буртика;

принимаем d₂ = 55 мм .

Длина вала под уплотнением:

l₂ » 1,25d₂ =1,25×55 = 68 мм.

Диаметр вала под подшипник:

d₄ = d₂ = 55 мм.

Диаметр вала под колесом:

d₃ = d₂ + 3,2r = 55+3,2×3,0 = 64,6 мм,

принимаем d₃ = 65 мм.

    Выбор подшипников.

Предварительно назначаем для быстроходного вала радиально-упорные роликоподшипники средней серии №27308, а для тихоходного вала роликоподшипники легкой широкой серии №7511

Таблица 2.

Размеры и характеристика выбранного подшипника

 

№	d, мм	D, мм	B, мм	C, кН	C0, кН	е	Y
27308	40	90	25	48,4	37,1	0,786	0,763
7511	55	100	27	80,0	61,0	0,36	1,666

       При установке радиально-упорных подшипников необходимо учитывать, что радиальные реакции считают приложенными к валу в точках пересечения нормалей, проведенных к серединам контактных площадок.

Для конических роликоподшипников поправка а:

а = В/2 + (d+D)e/6.

а₁ = 25/2+(40+90)∙0,786/6 = 29 мм.

а₂ = 27/2+(55+100)∙0,36/6 = 23 мм.

8 Расчетная схема валов редуктора

Схема нагружения быстроходного вала

 

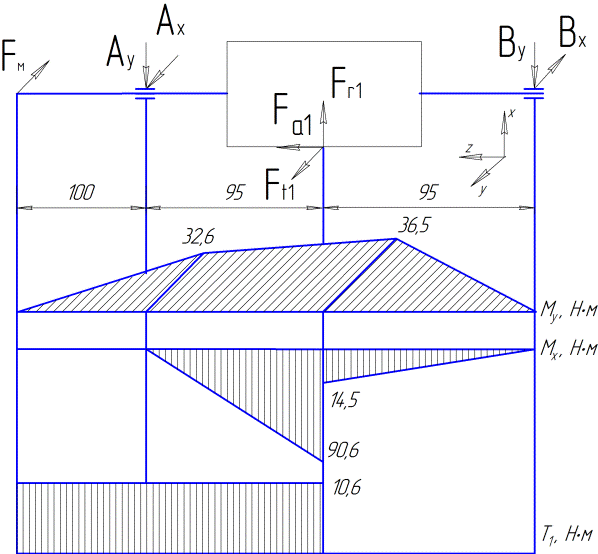
Рис. 8.1 Расчетная схема быстроходного вала.

 

Горизонтальная плоскость. Сумма моментов сил и реакций опор относительно опоры А

åm_A = 95F_t – 190B_X + F_м100 = 0

Отсюда находим реакцию опоры В в плоскости XOZ

B_X =(424·95 + 326·100)/190 = 384 H

Реакция опоры А в плоскости XOZ

A_X = B_X + F_М – F_t = 384 + 326 – 424 = 286 H

 

Изгибающие моменты в плоскости XOZ

M_X1 = 384·95 = 36,5 Н·м

M_X2 = 326·100= 32,6 Н·м

Вертикальная плоскость. Сумма моментов сил и реакций опор относительно опоры А

åm_A = 95F_r –190B_Y – F_a1d₁/2 = 0

Отсюда находим реакцию опор A и В в плоскости YOZ

B_Y = (1107·95 –3041·50,0/2)/190 = 153 H

A_Y = F_r – B_Y =1107 – 153 = 954 H

Изгибающие моменты в плоскости YOZ

M_Y = 153·95 = 14,5 Н·м

M_Y = 954·95 = 90,6 Н·м

Суммарные реакции опор:

А = (А_Х² + А_Y²)^0,5 = (286² + 954²)^0,5 = 996 H

B= (B_Х² + B_Y²)^0,5 = (384² + 153²)^0,5 = 413 H

   

 

        

Схема нагружения тихоходного вала

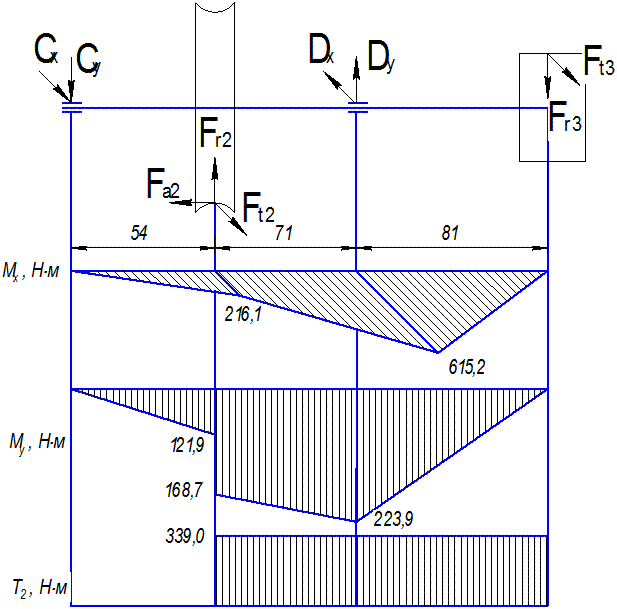
Рис. 8.2 Расчетная схема тихоходного вала.

 

Горизонтальная плоскость:

Sm_A = F_t3204 – D_x108 + F_t2 54 = 0;

D_х = (5631×204 + 3041×54)/108 =12157 Н;

C_х = D_x – F_t3 – F_t2 =12157 – 5631 – 3041 = 3485 Н;

Изгибающие моменты:

М_х1 = 3485×54 = 188,2 Н×м;  

М_х2 = 5631×96 = 540,6 Н×м.

 

 

   Вертикальная плоскость:

Sm_A = F_r2 54 + D_y108 – F_a2d₂/2 – F_r3204 = 0

D_y= (2050×204 –1107×54 – 424×200,0/2)/108 = 2926 Н

C_y=  F_r2+ D_y – F_r3   =1107+2926 –2050 = 1983 Н

М_y1 = 1983×54 =107,1 Н×м;  

М_y2 = 2050×96 = 196,8 Н×м;  

М_y3 = 2050×150 – 2926×54 =149,5 Н×м;  

 

  Суммарные реакции опор:

C = (C_x² +C_y²)^0,5 = (3485²+1983²)^0,5 = 4010 H,

D =  (12157²+2926²)^0,5 =12504 H,

 

   

9 Проверочный расчет подшипников

Быстроходный вал

    Эквивалентная нагрузка

P = (XVF_r + YF_a)K_бК_Т

       где Х – коэффициент радиальной нагрузки;

         Y – коэффициент осевой нагрузки;

         V = 1 – вращается внутреннее кольцо;

         F_r – радиальная нагрузка;

         Y – коэффициент осевой нагрузки;

         F_a – осевая нагрузка;

         K_б = 1,5 – коэффициент безопасности при нагрузке с умеренными     

                  толчками [1c214];

         К_Т = 1 – температурный коэффициент.

  Осевые составляющие реакций опор:

S_A = 0,83eA = 0,83×0,786×996= 650 H,

S_B = 0,83eB = 0,83×0,786×413 = 269 H.

  Результирующие осевые нагрузки:

F_aA = S_А = 650 H,

F_aВ = S_А+F_a =650 +3041 = 3691 H,

  Проверяем наиболее нагруженный подшипник В.

  Отношение F_a/F_r =  3691/413 =8,9 > e, следовательно Х=0,4; Y=0,763.

Р = (0,4×1,0×413 +0,763×3691)1,5×1,0 = 4225 Н.

 

Требуемая грузоподъемность подшипника

С_тр = Р(573wL/10⁶)^0,3 =

= 4225(573×96,3×30000/10⁶)^0,3 = 39,0 кH < C= 48,4 кН

   Условие С_тр  < C выполняется.

 

 

  Расчетная долговечность подшипников

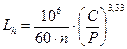= 10⁶(48,4×10³ /4225)^3,333/60×920 = 61344 часов,

больше ресурса работы привода, равного 30000 часов.

9.2 Тихоходный вал

 Эквивалентная нагрузка

 Осевые составляющие реакций опор:

S_C = 0,83eC = 0,83×0,360×4010 = 1198 H,

S_D = 0,83eD = 0,83×0,360×12504 = 3736 H.

Результирующие осевые нагрузки:

F_aC = S_C =1198 H,

F_aD = S_C + F_a =1198+ 424 = 1622 H.

Проверяем наиболее нагруженный подшипник D.

Отношение F_a/F_r=  1622/12504 = 0,13 < e, следовательно Х=1,0; Y=0.

Р = (1,0×1,0×12504+0)1,5×1,0 =18756 Н.

     Требуемая грузоподъемность подшипника:

С_тр = Р(573wL/10⁶)^0,3 =

=18756(573×2,41×30000/10⁶)^0,3 = 57,3 кH < C = 80,0 кН

 Условие С_тр  < C выполняется.

  Расчетная долговечность подшипников

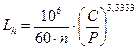= 10⁶(80,0×10³ /18756)^3,3333/60×23 = 91147 часов,

больше ресурса работы привода, равного 30000 часов.

 

10 Конструктивная компоновка привода