Технические системы целесообразно разделить на три класса:
1) Преобразования энергии;
2) Преобразования вещества и энергии;
3) Производства изделий.
1.2.6.1 Технические системы преобразования энергии
Это закрытые термодинамические системы, в которых как на входе, так и на выходе отсутствуют потоки вещества и через контрольную поверхность проходят только потоки энергии разного вида.
Соответственно в обоих частях уравнения эксергетического баланса системы (1.4) не будет членов, относящихся к потокам вещества ( 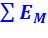 ).
).
К таким системам относят те, в которых протекает замкнутый процесс – цикл: тепловые насосы, холодильные установки.
Вместе с тем при анализе внутренних процессов преобразования энергии (внутри контрольной поверхности) в таких системах следует учитывать энергию и эксергию потоков вещества.
1.2.6.2 Технические системы преобразования вещества и энергии
Это открытые термодинамические системы, в которых как на входе, так и на выходе могут быть потоки и вещества, и энергии (например, эжектор, теплообменник). По существу это скорее отдельные элементы изучаемых термодинамических систем.
1.2.6.2 Технические системы производства изделий
В технических системах производства изделий на выходе получается такая продукция, ценность которой нельзя измерить в энергетических единицах – книги, автомобили, колбаса.
Однако, в технологической цепочке производства можно выделить элементы (подсистемы), в которых на входе и выходе имеются только потоки вещества и энергии. В этом случае производится оценка термодинамической эффективности (эксергетическим методом) и совершенствование соответствующих подсистем, а, следовательно, и системы в целом.
1.3 Термодинамический анализ и его приложение к техническим системам
Эксергетический баланс технической системы и ее частей определяет все происходящие в ней превращения энергии и веществ.
С помощью эксергетического баланса возможно определить:
1) Распределение и характеристики потерь;
2) Значения КПД отдельных частей и системы в целом;
3) Долю каждой части и характеристики связей между ними;
4) Взаимодействие системы с окружающей средой.
Эта информация может служить для дальнейшей работы по усовершенствованию системы.
Особое значение имеет раздельное определение внутренних 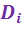 и внешних
и внешних 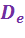 потерь эксергии.
потерь эксергии.
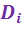 – отражают несовершенство внутренних преобразований вещества и энергии в системе.
– отражают несовершенство внутренних преобразований вещества и энергии в системе.
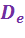 – отражают несовершенство преобразований вещества и энергии при взаимодействии системы с окружающей средой.
– отражают несовершенство преобразований вещества и энергии при взаимодействии системы с окружающей средой.
Эксергетический баланс дает возможность установить предельные значения, до которых может быть снижена эксергиявещества и энергии на выходе из системы для получения заданного результата.
В идеальном случае, достижение максимального эксергетического КПД, согласно уравнению (1.3), 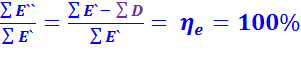 , возможно при отсутствии потерь эксергии
, возможно при отсутствии потерь эксергии 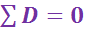 .
.
Минимальное значение 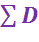 определяется технически достижимым
определяется технически достижимым 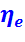 .
.
Анализ технических систем на основе эксергетического баланса возможен на всех стадиях проектирования и эксплуатации систем с целью их оптимизации.
Термодинамическая оптимизация системы сводится к тому, чтобы, изменяя те или иные ее параметры или структуру, получить как можно большую ее термодинамическую эффективность, т.е. максимальный 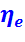 .
.
Термодинамическая оптимизация не всегда должна проводиться на базе эксергетического баланса.
Существует ряд систем, например, теплосиловые паротурбинные и газотурбинные установки, предназначенные только для выработки механической энергии (преобразуемой затем в электрическую).
В этом случае эффективный термический КПД 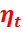 (определенный как отношение мощности на выходе к теплотворной способности топлива на входе) будет мало отличаться от эксергетического КПД
(определенный как отношение мощности на выходе к теплотворной способности топлива на входе) будет мало отличаться от эксергетического КПД 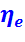 .
.
По сути, эффективный термический КПД 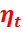 является коэффициентом преобразования энергии в теплосиловой установке, и его экстремум будет находиться там же, где экстремум
является коэффициентом преобразования энергии в теплосиловой установке, и его экстремум будет находиться там же, где экстремум 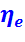 .
.
ТДЭФФ-2
ЦИКЛЫ ДВИГАТЕЛЕЙ ВНУТРЕННЕГО СГОРАНИЯ
Общие сведения
До 70-80-х годов 19 века единственным источником механической работы являлась паровая машина с низким термическим КПД установки.
Машины, где топливо сжигается непосредственно в цилиндре под поршнем, наз. двигателями внутреннего сгорания (ДВС).
В 1877 г. немецкий инженер Отто построил бензиновый двигатель.
В 1897 г. немецкий инженер Дизель разработал двигатель высокого сжатия, работавший на керосине, который распылялся в цилиндре воздухом высокого давления от компрессора.
Инженер Мамин в 1893 г. создал двигатель высокого сжатия, работавший на сырой нефти при бескомпрессорном механическом распылении топлива.
В 1904 г. русский инженер Тринклер построил бескомпрессорный двигатель, в котором сгорание топлива сначала происходило при постоянном объеме, а затем при постоянном давлении. Такой двигатель со смешенным сгоранием топлива получил широкое распространение во всем мире.
Все современные поршневые ДВС разделяют на 3 группы:
1) С быстрым сгоранием топлива при постоянном объеме  ;
;
2) С постепенным сгоранием топлива при постоянном давлении  ;
;
3) Со смешанным сгоранием топлива частично при постоянном объеме  и частично при постоянном давлении
и частично при постоянном давлении  .
.
При исследованиях идеальных термодинамических циклов поршневых ДВС обычно определяют:
Ø Количество подведенной и отведенной теплоты;
Ø Основные параметры состояния в типичных точках цикла;
Ø Термический КПД цикла;
Ø Производят анализ термического КПД.
Основными характеристиками или параметрами любого цикла ДВС являются следующие безразмерные величины:
С т е п е н ь с ж а т и я:
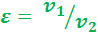 (2.1)
(2.1)
Отношение начального удельного объема рабочего тела к его удельному объему в конце сжатия.
С т е п е н ь п о в ы ш е н и я д а в л е н и я:
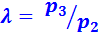 (2.2)
(2.2)
Отношение давлений в конце и в начале изохорного процесса подвода теплоты.
С т е п е н ь п р е д в а р и т е л ь н о г о р а с ш и р е н и я или с т е п е н ь и з о б а р н о г о р а с ш и р е н и я:
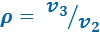 (2.3)
(2.3)
Отношение объемов в конце и в начале изобарного подвода теплоты.
2.2 Цикл с подводом теплоты в процессе 
Исследование работы реального поршневого двигателя производят по индикаторной диаграмме, на которой приводится изменение давления в цилиндре, в зависимости от положения поршня за весь цикл.
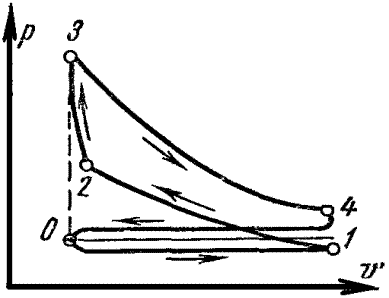
Рис. 2.1 Индикаторная диаграмма реального поршневого двигателя с быстрым сгоранием топлива при 
В качестве топлива в таких двигателях применяют легкие топлива: бензин, спирт, генераторный или светильный газ.
0-1 – линия всасывания. При ходе поршня из левого «мертвого» положения в крайне правое – засасывается горючая смесь, состоящая из паров, мелких частиц топлива и воздуха. 0-1 – не является термодинамическим процессом – не изменяются основные параметры, изменяется массовое количество и объем смеси в цилиндре.
1-2 – линия сжатия. При обратном движении поршня всасывающий клапан закрывается и происходит сжатие смеси.
В т.2, когда поршень немного не дошел до левого «мертвого» положения – происходит воспламенение горючей смеси от электрической искры.
2-3 – почти мгновенное сгорание горючей смеси (практически при постоянном объеме). В результате сгорания топлива температура газа резко возрастает и давление увеличивается – т.3
3-4 – линия расширения. Поршень перемещается в правое «мертвое» положение – газы расширяются и совершают полезную работу.
В т.4 открывается выхлопной клапан и давление в цилиндре падает почти до наружного давления.
4-0 – линия выхлопа. При дальнейшем движении поршня справа налево из цилиндра удаляются продукты сгорания через выхлопной клапан при давлении несколько превышающем атмосферное.
Рабочий процесс реального двигателя совершается за четыре хода поршня – такта или за два оборота вала. Такие ДВС наз. четырехтактными.
Цикл реального ДВС не является замкнутым и состоит из необратимых процессов, т.к. имеют место:
¾ Трение;
¾ Химические реакции в рабочем теле;
¾ Конечные значения скоростей поршня;
¾ Теплообмен при конечной разности температур, и т.д.
Анализ такого цикла с точки зрения теории тепловых процессов невозможен.
Поэтому термодинамика исследует идеальные циклы ДВС, состоящие из обратимых процессов.
Допущения при исследованиях:
1. Рабочее тело – идеальный газ с постоянной теплоемкостью;
2. Цилиндр заполнен постоянным количеством рабочего тела;
3. Подвод теплоты к рабочему телу осуществляется не за счет сжигания топлива, а от внешних источников;
4. Разность температур между источником теплоты и рабочим телом - бесконечно мала;
5. Разность температур между приемником теплоты и рабочим телом - бесконечно мала;
Изучение идеальных термодинамических циклов позволяет производить при принятых допущениях анализ и сравнение работы различных ДВС, их экономичность.
|
|
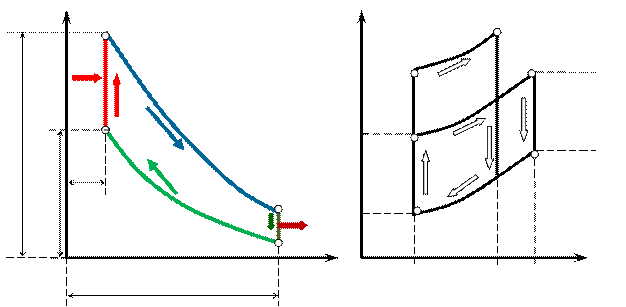
Рис. 2.2 Идеальный цикл ДВС с подводом теплоты в процессе  в pv- TS-координатах
в pv- TS-координатах
Рассмотрим идеальный термодинамический цикл, состоящий из двух изохор и двух адиабат.
Идеальный газ с начальными параметрами p 1, v 1, и T 1 сжимается по адиабате 1-2 то т.2.
По изохоре 2-3 рабочему телу сообщается количество теплоты q 1.
Рабочее тело расширяется по адиабате 3-4.
По изохоре 4-1 рабочее тело возвращается в первоначальное состояние и при этом отводится теплота q 2 в теплоприемник.
Характеристиками цикла являются: степень сжатия 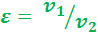 и степень повышения давления
и степень повышения давления 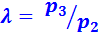 .
.
Определяем термический КПД цикла, считая, что изохорная теплоемкость 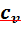 и величина k постоянны:
и величина k постоянны:
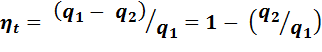
Количество подведенной теплоты:
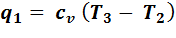 ,
,
Количество отведенной теплоты:
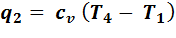
Тогда термический КПД цикла:
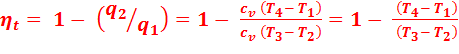 (2.4)
(2.4)
Параметры рабочего тела во всех характерных точках цикла:
В точке 2:
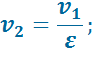
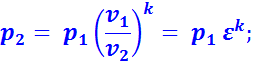
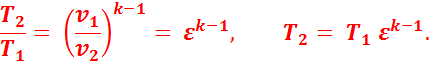
В точке 3:
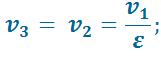
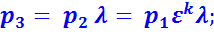
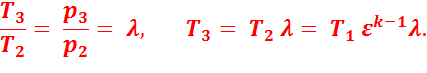
В точке 4:
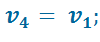
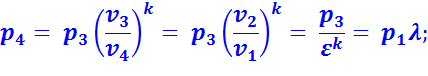
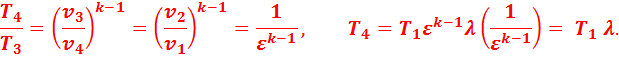
Подставив найденные значения температур в уравнение (2.4), получим:
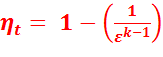 (2.5)
(2.5)
Из уравнения (2.5) следует, что термический КПД такого цикла зависит от степени сжатия 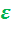 и показателя адиабаты k, т.е. от природы рабочего тела. От степени повышения давления
и показателя адиабаты k, т.е. от природы рабочего тела. От степени повышения давления 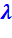 КПД этого цикла не зависит.
КПД этого цикла не зависит.
В таблице 2.1 приведены величины термического КПД цикла с быстрым сгоранием топлива при  при различных значениях
при различных значениях 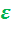 и k.
и k.
Таблица 2.1
|
|
| |
| k = 1,35 | k = 1,4 | |
| 3 | 32,0 | 36,0 |
| 4 | 38,0 | 43,0 |
| 5 | 42,5 | 47,5 |
| 6 | 46,5 | 51,5 |
| 7 | 49,4 | 55,0 |
| 8 | 51,7 | 57,0 |
| 10 | 55,2 | 61,5 |
По TS-диаграмме КПД определим из соотношения площадей:
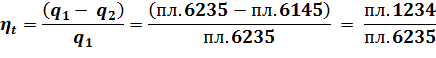
При равенстве количеств теплоты, подведенных в двух циклах, пл. 67810 = пл. 6235, но при разных степенях сжатия КПД будет больше у цикла с большей степенью сжатия, т.к. в теплоприемник отводится меньшее количество теплоты:
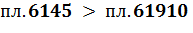
Увеличение степени сжатия ограничивается опасностью преждевременного воспламенения смеси, а также высокой скорости сгорания, что может вызвать детонацию (взрывное горение).
Для каждого топлива должна применяться оптимальная степень сжатия. В зависимости от вида топлива степень сжатия в этих двигателях:
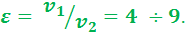
КПД двигателей с подводом теплоты при  невысок.
невысок.
Теоретическая полезная работа 1 кг рабочего тела:
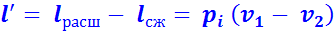 (2.6)
(2.6)
Величину 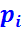 наз. средним индикаторным давлением. Это условное постоянное давление под действием которого поршень в течение одного хода совершает работу, равную работе всего цикла.
наз. средним индикаторным давлением. Это условное постоянное давление под действием которого поршень в течение одного хода совершает работу, равную работе всего цикла.
Для цикла с подводом теплоты при  среднее индикаторное давление:
среднее индикаторное давление:
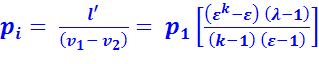 (2.7)
(2.7)
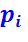 возрастает с увеличением:
возрастает с увеличением: 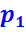 ;
; 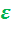 ;
; 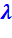 .
.
Теоретическая полезная работа 1 кг рабочего тела также:
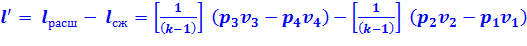 (2.8)
(2.8)
2.3 Цикл с подводом теплоты в процессе 
Исследование циклов с подводом теплоты при  показало, что для повышения экономичности таких двигателей необходимо применять высокие степени сжатия.
показало, что для повышения экономичности таких двигателей необходимо применять высокие степени сжатия.
Степень сжатия ограничивается температурой самовоспламенения горючей смеси.
Если произвести раздельное сжатие воздуха и топлива – это ограничение отпадает.
Воздух при большом сжатии имеет настолько высокую температуру, что подаваемое в цилиндр топливо самовоспламеняется без всяких запальных приспособлений.
Раздельное сжатие воздуха и топлива позволяет использовать любое жидкое тяжелое и дешовое топливо – мазут, нефть, смолы, каменноугольные масла.
Такое раздельное сжатие воздуха и топлива осуществляется в двигателях, работающих с постепенным сгоранием топлива при постоянном давлении.
Воздух сжимается в цилиндре двигателя, а жидкое топливо распыляется сжатым воздухом от компрессора.
Раздельное сжатие позволяет применять высокие степени сжатия: (до 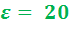 ) и исключает преждевременное самовоспламенение топлива.
) и исключает преждевременное самовоспламенение топлива.
Процесс горения топлива при постоянном давлении обеспечивается регулировкой топливной форсунки ( ДВС Дизеля).
Рассмотрим идеальный цикл ДВС с постепенным сгоранием топлива при постоянном давлении и с подводом теплоты при  .
.
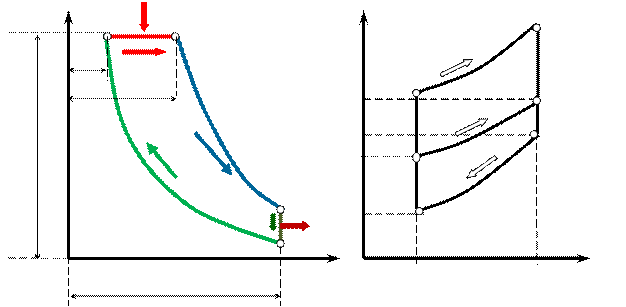
Рис. 2.3 Идеальный цикл ДВС с подводом теплоты в процессе  в pv- TS-координатах
в pv- TS-координатах
Идеальный газ с начальными параметрами p 1, v 1, и T 1 сжимается по адиабате 1-2 то т.2.
По изобаре 2-3 рабочему телу сообщается количество теплоты q 1.
От т.3 рабочее тело расширяется по адиабате 3-4.
По изохоре 4-1 рабочее тело возвращается в первоначальное состояние и при этом отводится теплота q 2 в теплоприемник.
Характеристиками цикла являются: степень сжатия 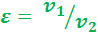 и степень предварительного расширения
и степень предварительного расширения 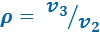 .
.
Определяем термический КПД цикла, считая, что теплоемкости 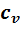 и
и 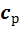 , а также величина k =
, а также величина k = 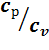 постоянны:
постоянны:
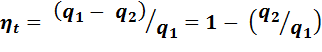
Количество подведенной теплоты:
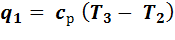 ,
,
Количество отведенной теплоты:
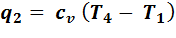
Тогда термический КПД цикла:
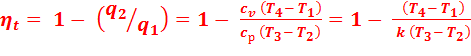 (2.8)
(2.8)
Параметры рабочего тела во всех характерных точках цикла:
В точке 2:
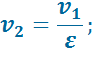
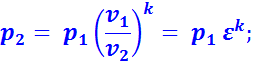
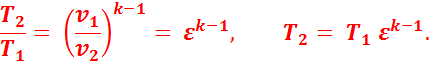
В точке 3:
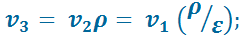
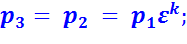
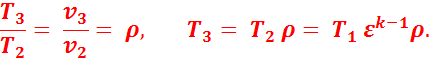
В точке 4:
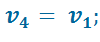
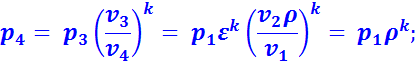
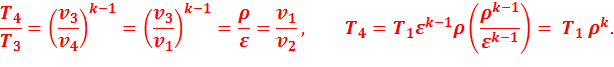
Подставив найденные значения температур в уравнение (2.8), получим:
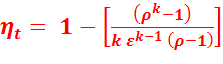 (2.9)
(2.9)
Из уравнения (2.9) следует, что термический КПД такого цикла зависит от степени сжатия 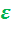 , показателя адиабаты k, т.е. от природы рабочего тела и степени предварительного расширения
, показателя адиабаты k, т.е. от природы рабочего тела и степени предварительного расширения 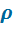 . С увеличением
. С увеличением 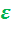 и k – КПД этого цикла увеличивается, а с увеличением
и k – КПД этого цикла увеличивается, а с увеличением 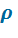 – уменьшается.
– уменьшается.
В таблице 2.2 приведены величины термического КПД цикла с подводом теплоты при  при различных значениях
при различных значениях 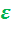 и
и 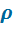 при k = 1,35.
при k = 1,35.
Таблица 2.2
|
|
|
|
| |
При 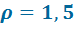
| При 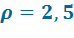
| |||
| 10 | 52,0 | 46,0 | - | - |
| 12 | 54,0 | 49,0 | 25,7 | 907 |
| 14 | 57,0 | 52,0 | 31,8 | 956 |
| 16 | 59,0 | 54,0 | 41,4 | 1020 |
| 18 | 61,9 | 56,7 | - | - |
| 20 | 63,0 | 56,0 | - | - |
По TS-диаграмме КПД определим из соотношения площадей:
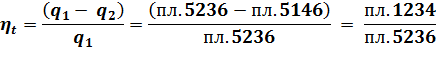
При равенстве площадей отведенной теплоты в теплоприемник (пл.5146), КПД будет больше у цикла с большей степенью сжатия, т.к. площадь его полезной работы будет больше:
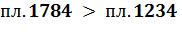
Для цикла с подводом теплоты при  среднее индикаторное давление:
среднее индикаторное давление:
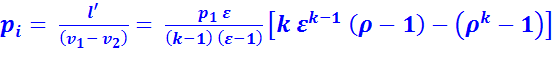 (2.10)
(2.10)
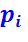 возрастает с увеличением:
возрастает с увеличением: 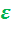 и
и 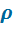 .
.
Теоретическая полезная работа 1 кг рабочего тела за один цикл:
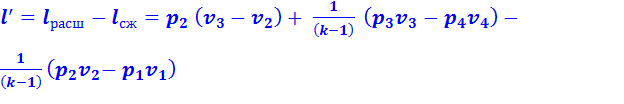 (2.11)
(2.11)
2.4 Цикл с подводом теплоты в процессе при  и
и  , или цикл со смешанным подводом теплоты
, или цикл со смешанным подводом теплоты
Двигатели с постепенным сгоранием топлива при  имеют ряд недостатков:
имеют ряд недостатков:
§ На работу компрессора (для подачи топлива) расходуется 6 – 10% мощности двигателя;
§ Наличие компрессора усложняет конструкцию и уменьшает экономичность работы двигателя;
§ Сложные устройства насоса и форсунки;
§ Установка имеет значительнеый вес.
Г.В. Тринклер создал бескомпрессорный двигатель высокого сжатия с механическим распылением топлива при давлениях 500-700 бар, лишенный недостатков обоих приведенных типов двигателей.
Жидкое топливо топливным насосом подается через топливную форсунку в головку цилиндра (или в специальную предкамеру) в виде мельчайших капелек.
Попадая в нагретый воздух, топливо самовоспламеняется и горит в течение всего периода, пока открыта форсунка: вначале при  , а затем при
, а затем при  .
.
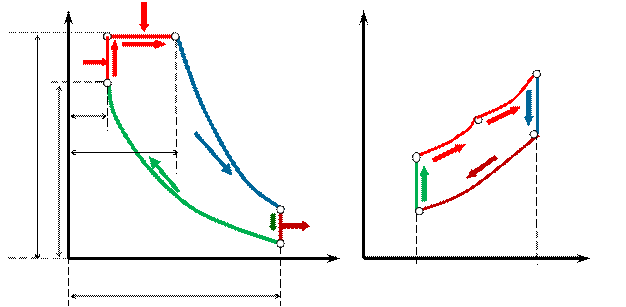
Рис. 2.4 Идеальный цикл ДВС с подводом теплоты в процессе при  и
и  в pv- TS-координатах
в pv- TS-координатах
Идеальный газ с начальными параметрами p 1, v 1, и T 1 сжимается по адиабате 1-2 то т.2.
По изохоре 2-3 рабочему телу сообщается первая доля теплоты q 1 ′.
По изобаре 3-4 подводится вторая доля теплоты q 1 ′′.
От т.4 рабочее тело расширяется по адиабате 4-5.
По изохоре 5-1 рабочее тело возвращается в первоначальное состояние в т.1 и при этом отводится теплота q 2 в теплоприемник.
Характеристиками цикла являются: степень сжатия 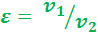 , степень повышения давления
, степень повышения давления 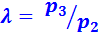 и степень предварительного расширения
и степень предварительного расширения 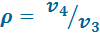 .
.
Определяем термический КПД цикла, считая, что теплоемкости 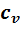 и
и 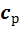 , а также величина k =
, а также величина k = 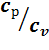 постоянны:
постоянны:
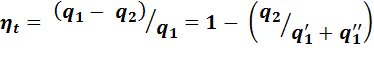
Первая доля подведенной теплоты:
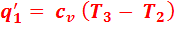 ,
,
Вторая доля подведенной теплоты:
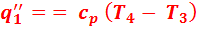
Количество отведенной теплоты:
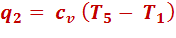
Тогда термический КПД цикла:
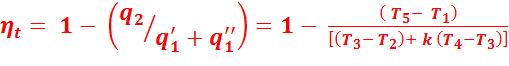 (2.12)
(2.12)
Параметры рабочего тела во всех характерных точках цикла:
В точке 2:
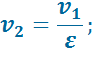
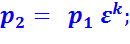
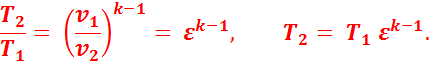
В точке 3:
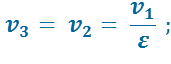
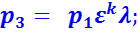
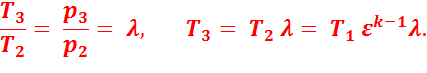
В точке 4:
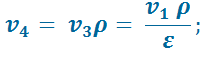
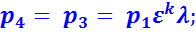
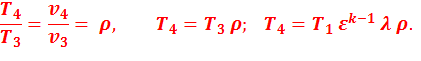
В точке 5:
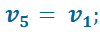
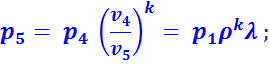
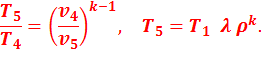
Подставив найденные значения температур в уравнение (2.13), получим:
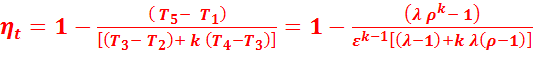 (2.14)
(2.14)
Из уравнения (2.14) следует, что термический КПД такого цикла зависит от степени сжатия 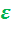 , степени повышения давления
, степени повышения давления 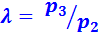 , степени предварительного расширения
, степени предварительного расширения 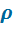 и показателя адиабаты k, т.е. от природы рабочего тела.
и показателя адиабаты k, т.е. от природы рабочего тела.
С увеличением 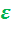 ,
, 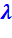 и k – КПД этого цикла увеличивается, а с увеличением
и k – КПД этого цикла увеличивается, а с увеличением 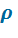 – уменьшается.
– уменьшается.
По TS-диаграмме КПД определим из соотношения площадей:
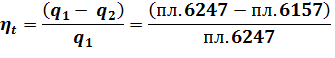
Для этих двигателей обычно принимают:
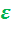 = 10 – 14;
= 10 – 14;
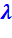 = 1,2 – 1,7;
= 1,2 – 1,7;
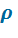 = 1,1 – 1,5;
= 1,1 – 1,5;
Теоретическая полезная работа 1 кг рабочего тела за один цикл:
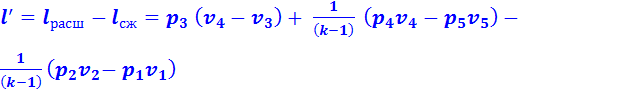 (2.15)
(2.15)
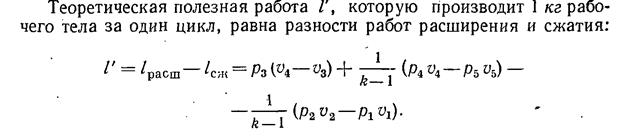
Для цикла со смешанным подводом теплоты среднее индикаторное давление:
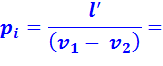
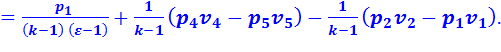 (2.16)
(2.16)
Дата: 2019-02-25, просмотров: 400.
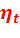
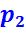 , бар
, бар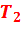 , К
, К