Термодинамическая эффективность теплового оборудования и ТЕПЛОМАССООБМЕННЫХ ПРОЦЕССОВ В НЕМ
ВВЕДЕНИЕ
Весьма обобщенно, задача теплотехника, – создать эффективные способы массового производства и использования энергии различных видов.
Наука - «теплотехника» или область практической деятельности по использованию результатов фундаментальной науки?
Ответ на этот вопрос зависит от того, как мы расшифровываем термин "эффективный способ", от принятых критериев эффективности. Если на первый план выдвигаются экономические критерии, такие как себестоимость произведенной энергии или прибыльность производства, то «теплотехника» есть область предпринимательства в сфере реализации научных знаний.
Если же за критерии брать натуральные показатели, такие как расходы сырья и энергии на получение единичного количества продукта (различных видов энергии) и интенсивность процессов (скорость трансформации вещества и энергии в единичном объеме аппаратуры), то задачи, стоящие перед теплотехником, представляются как сугубо научные: создать такие системы, в которых единичное количество продукта (энергии, транспортируемого вещества) производится из минимального количества сырья, при минимальном потреблении энергии и при максимальной скорости процесса. При этом теплотехник действует в рамках, предопределенных фундаментальными законами природы.
И в этом смысле теплотехника есть часть науки, естественное продолжение или расширение термодинамики и теории тепломассообмена, но с опорой в равной степени и на макроскопическую физику и механику.
Вышесказанное объясняет, почему изучение показателей термодинамической эффективности теплового оборудования и тепломассообменных процессов в нем особенно важно.
Основное внимание в предлагаемом курсе уделяется наиболее "наукоемким" критериям, характеризующим степень термодинамического совершенства теплового оборудования и тепломассообменных процессов в нем.
Выделение этого вопроса продиктовано тем значением для устойчивого развития цивилизации, которое приобретают в современную эпоху проблемы ресурсо- и энергосбережения и снижения антропогенного воздействия на окружающую среду. Выпускниками академии вопросы ресурсо- и энергосбережения должны пониматься не на общегражданском уровне контроля за показаниями счетчиков воды, газа и электричества, а на фундаментальном уровне второго начала термодинамики, уровне управления процессами генерации энтропии.
Содержание этой части курса неизбежно пересекается с содержанием предшествующего курса – "Техническая термодинамика".
В приложении к проблемам теплогазоснабжения, вентиляции и кондиционирования положения термодинамики предстают перед изучающим предмет в новых "одеждах", а именно, в "потоковом" выражении. Уравнения термодинамики характеризуют теперь изменение состояния не статичной порции вещества, а потока вещества, проходящего через технологическую систему. Аналогичным образом вместо количеств энергии, теплоты или работы, воспринимаемых (отдаваемых) порцией вещества, в термодинамическую модель технологической системы входят потоки теплоты и работы и скорости возникновения энтропии в системе.
Как раз в приложении к задачам технологии такие ключевые абстрактные понятия термодинамики как полезная работа системы и максимальная работа системы приобретают совершенно конкретное и ясное содержание.
Таким же конкретным и ясным содержанием наполняется понятие скорости возникновения энтропии. Центральное уравнение термодинамики неравновесных процессов, выражающее скорость роста энтропии как сумму произведений потоков и движущих сил, позволяет вовлечь весь арсенал макроскопической механики, и физики в дело разработки термодинамически более совершенных технологических систем.
В курсе лекций принята терминология, рекомендованная Комитетом научно-технической терминологии АН СССР, (Термодинамика, Сб. определений, Вып. 103, Изд-во "Наука", М. 1984) и обозначения, рекомендованные (Quantities, Units and Symbols in Physical Chemistry, 2nd Edition, IUPAC, 1993).
ТДЭФФ-1
ТЕРМОДИНАМИЧЕСКИЙ АНАЛИЗ И ЕГО ПРИЛОЖЕНИЕ К ОЦЕНКЕ ЭФФЕКТИВНОСТИ ТЕПЛОТЕХНИЧЕСКОГО ОБОРУДОВАНИЯ
II группа энергий:
Виды энергий, которые не могут быть полностью преобразованы в любой др. вид энергии. Виды энергии II группы имеют энтропию отличную от нуля: S > 0. Энергию таких видов наз. «неорганизованной» или «энтропийной».
Согласно ВТОРОМУ НАЧАЛУ ТЕРМОДИНАМИКИ, в системе могут протекать только такие процессы преобразования энергии, в которых суммарная энтропия участвующих в нем тел или возрастает или (в обратимых процессах) остается постоянной (ΔS ≥ 0).
Следовательно, все виды «безэнтропийной» энергии (I группа) способны к любым превращениям, т.к. при любом превращении энергии энтропия будет либо возрастать либо оставаться постоянной.
Для видов энергии II группы однозначно невозможно превращение полностью в какой либо вид «безэнтропийной» энергии.
Любой вид «безэнтропийной» энергии, обладающий неограниченной превращаемостью, с технической точки зрения ценнее «качественнее», чем любой вид «энтропийной» энергии.
Это утверждение справедливо как для видов энергии, носителями которой являются транспортируемые тела (например, внутренняя энергия вещества – горячей воды), так и для видов энергии, находящихся в процессе перехода от одних тел к другим (тепло и работа любого вида).
Таблица 1.1 – Возможности взаимного преобразования видов энергии
| № п/п | 1. Механическая | 2. Электрическая | 3. Молекулярная | 4. Химическая | 6. Энергия в переходе - Теплота | 7. Энергия в переходе - Работа |
| ☺ | ☺ | ☺ | ☺ | ☺ | ☺ |
| ☺ | ☺ | ☺ | ☺ | ☺ | ☺ |
| ☻ | ☻ | ☺ | ☻ | ☺ | ☻ |
| ☻ | ☻ | ☺ | ☻ | ☺ | ☻ |
| ☺ | ☺ | ☺ | ☺ | ☺ | ☺ |
| ☻ | ☻ | ☺ | ☻ | ☻ | ☻ |
| ☺ | ☺ | ☺ | ☺ | ☺ | ☺ |
☺- Полное преобразование видов энергии I группы в энергию II группы;
☻- неполное преобразование.
Механическая, электрическая, ядерные (количество выделяющейся энергии при ядерных реакциях настолько велико, что энтропийной составляющей можно пренебречь) энергии и работа – относятся к I группе.
Молекулярная и химическая энергии, а также теплота – ко II группе. Все виды энергии I группы при взаимных преобразованиях полностью превращаются один в другой независимо от параметров окружающей среды.
В случае преобразования энергий II группы – чем меньше разность интенсивных параметров среды и рабочего тела технической системы – тем меньшая часть энергии может быть преобразована.
При равенстве параметров рабочего тела системы и окружающей среды – преобразование энергии невозможно.
1.2.3 Определение эксергии
Эксергия – является мерой, позволяющей оценить энергию (ее превращаемость) с учетом ее качественных характеристик.
Эксергия – это количество работы, которое может быть получено внешним приемником энергии при обратимом взаимодействии термодинамической системы или потока энергии с окружающей средой до установления полного равновесия.
Система, для анализа которой используется эксергетический метод, может быть простой (например, рабочее тело в замкнутом объеме) и сложной (энергетический агрегат, комплекс агрегатов, отрасль, регион).
Система может быть закрытой (без обмена веществ с внешней средой) и открытой (при существовании такого обмена).
Система может быть стационарной (с параметрами, не изменяющимися во времени) и нестационарной.
Эксергия системы определяется не только действием системы, но и одновременным действием окружающей среды (сосуд с газом, давление которого меньше атмосферного).
При полном равновесии системы и среды – эксергия равна нулю. Такое состояние системы наз. нулевым – в англояз. литературе мертвым состоянием.
Работа, которая согласно определению эксергии служит ее мерой, не обязательно является необходимым конечным результатом, т.е. целью действия анализируемой системы или потока энергии. Конечным результатом такого действия кроме работы могут быть преобразование и получение какого-либо вещества, теплоты, холода, излучения нужных параметров и т.д.
Поэтому в определении эксергии слово «работа» используется только как мера такой энергии, но не как обязательная конечная цель энергетических превращений.
Согласно ПЕРВОМУ и ВТОРОМУ НАЧАЛАМ ТЕРМОДИНАМИКИ в каждом данном сосотоянии эксергия системы, так же как и ее энергия, имеет определенное фиксированное значение, поскольку обратимый процесс выравнивания ее интенсивных параметров с параметрами окружающей среды однозначно характеризуется работой.
Взаимодействие системы с окружающей средой может проходить как обратимо (идеальный процесс), так и необратимо (реальный процесс).
В результате идеального процесса (по определению эксергии) получается работа, равная эксергии.
В реальном процессе работа меньше убыли эксергии (в пределе работа может быть равна нулю), т.к. часть ее не превращается в работу, а исчезает.
В этом сосотоит существенное отличие эксергии от энергии:
В любом процессе энергия подчинается закону сохранения.
Эксергия подчиняется закону сохранения только в обратимых процессах, в реальных процессах она может частично или полностью исчезать, теряться в результате диссипации энергии в необратимых процессах.
При прочих равных условиях чем меньше эта потеря эксергии, тем процесс более термодинамически совершенен, т.е. тем больше его термодинамическая эффективность.
Эксергетический баланс
Уравнение эксергетического баланса универсально и пригодно для любых термодинамических систем, независимо от видов энергии, участвующих в процессе:
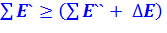 (1.1)
(1.1)
Или
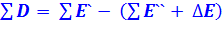 (1.1а)
(1.1а)
Здесь 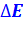 - приращение эксергии системы между начальной и конечной точками процесса;
- приращение эксергии системы между начальной и конечной точками процесса;
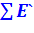 и
и 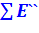 - суммарная эксергия в начальной и конечной точке процесса, соответственно;
- суммарная эксергия в начальной и конечной точке процесса, соответственно;
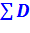 - суммарная потеря эксергии от необратимости процесса.
- суммарная потеря эксергии от необратимости процесса.
Для стационарного во времени процесса 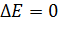 и
и 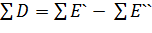 .
.
Соответствующее уравнение энергетического баланса:
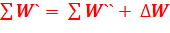 (1.2)
(1.2)
Здесь 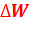 - приращение энергии системы между начальной и конечной точками процесса;
- приращение энергии системы между начальной и конечной точками процесса;
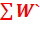 и
и 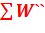 - суммарная энергия в начальной и конечной точке процесса, соответственно;
- суммарная энергия в начальной и конечной точке процесса, соответственно;
Принципиальная разница между уравнениями (1.1) и (1.2) состоит в том, что в (1.2) при любых условиях равенство правой и левой частей соблюдается, а в (1.1) левая часть в реальных процессах всегда больше правой.
Таким образом, энергетический балансне может отразить потери от необратимости процессов в рассматриваемой системе, т.к. независимо от степени ее совершенства уравнение (1.2) будет всегда справедливо.
Эксеретический баланс во всех случаях показывает потери от необратимости в системе. Степень ее термодинамического совершенства (эксергетический КПД) также определяется однозначно отношением:
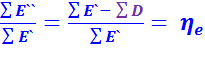 (1.3)
(1.3)
Термины «потери энергии» и «потери эксергии» имеют принципиально разное содержание.
«Потери энергии» - означает не потерю энергии вообще (Энергия не исчезает), а потерю ее для данной системы или данной цели, если часть энергии непригодна для нее по своей форме или параметрам.
«Потери эксергии» - означает полное исчезновение эксергии, т.е. ее уничтожение, связанное с диссипацией энергии.
В соответствии с методикой эксергетического анализа величины 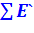 и
и 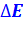 – включают эксергию тех видов вещества и энергии, которые входят в энергетический баланс рассматриваемой системы.
– включают эксергию тех видов вещества и энергии, которые входят в энергетический баланс рассматриваемой системы.
Как правило, это эксергия потока рабочего тела 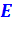 , эксергия теплового потока
, эксергия теплового потока 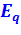 и работа L (равная энергии W для механической и электрической энергии).
и работа L (равная энергии W для механической и электрической энергии).
ТДЭФФ-2
ЦИКЛЫ ДВИГАТЕЛЕЙ ВНУТРЕННЕГО СГОРАНИЯ
Общие сведения
До 70-80-х годов 19 века единственным источником механической работы являлась паровая машина с низким термическим КПД установки.
Машины, где топливо сжигается непосредственно в цилиндре под поршнем, наз. двигателями внутреннего сгорания (ДВС).
В 1877 г. немецкий инженер Отто построил бензиновый двигатель.
В 1897 г. немецкий инженер Дизель разработал двигатель высокого сжатия, работавший на керосине, который распылялся в цилиндре воздухом высокого давления от компрессора.
Инженер Мамин в 1893 г. создал двигатель высокого сжатия, работавший на сырой нефти при бескомпрессорном механическом распылении топлива.
В 1904 г. русский инженер Тринклер построил бескомпрессорный двигатель, в котором сгорание топлива сначала происходило при постоянном объеме, а затем при постоянном давлении. Такой двигатель со смешенным сгоранием топлива получил широкое распространение во всем мире.
Все современные поршневые ДВС разделяют на 3 группы:
1) С быстрым сгоранием топлива при постоянном объеме  ;
;
2) С постепенным сгоранием топлива при постоянном давлении  ;
;
3) Со смешанным сгоранием топлива частично при постоянном объеме  и частично при постоянном давлении
и частично при постоянном давлении  .
.
При исследованиях идеальных термодинамических циклов поршневых ДВС обычно определяют:
Ø Количество подведенной и отведенной теплоты;
Ø Основные параметры состояния в типичных точках цикла;
Ø Термический КПД цикла;
Ø Производят анализ термического КПД.
Основными характеристиками или параметрами любого цикла ДВС являются следующие безразмерные величины:
С т е п е н ь с ж а т и я:
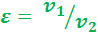 (2.1)
(2.1)
Отношение начального удельного объема рабочего тела к его удельному объему в конце сжатия.
С т е п е н ь п о в ы ш е н и я д а в л е н и я:
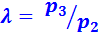 (2.2)
(2.2)
Отношение давлений в конце и в начале изохорного процесса подвода теплоты.
С т е п е н ь п р е д в а р и т е л ь н о г о р а с ш и р е н и я или с т е п е н ь и з о б а р н о г о р а с ш и р е н и я:
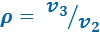 (2.3)
(2.3)
Отношение объемов в конце и в начале изобарного подвода теплоты.
2.2 Цикл с подводом теплоты в процессе 
Исследование работы реального поршневого двигателя производят по индикаторной диаграмме, на которой приводится изменение давления в цилиндре, в зависимости от положения поршня за весь цикл.
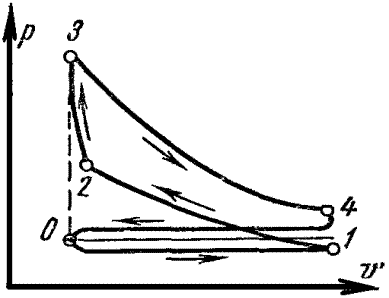
Рис. 2.1 Индикаторная диаграмма реального поршневого двигателя с быстрым сгоранием топлива при 
В качестве топлива в таких двигателях применяют легкие топлива: бензин, спирт, генераторный или светильный газ.
0-1 – линия всасывания. При ходе поршня из левого «мертвого» положения в крайне правое – засасывается горючая смесь, состоящая из паров, мелких частиц топлива и воздуха. 0-1 – не является термодинамическим процессом – не изменяются основные параметры, изменяется массовое количество и объем смеси в цилиндре.
1-2 – линия сжатия. При обратном движении поршня всасывающий клапан закрывается и происходит сжатие смеси.
В т.2, когда поршень немного не дошел до левого «мертвого» положения – происходит воспламенение горючей смеси от электрической искры.
2-3 – почти мгновенное сгорание горючей смеси (практически при постоянном объеме). В результате сгорания топлива температура газа резко возрастает и давление увеличивается – т.3
3-4 – линия расширения. Поршень перемещается в правое «мертвое» положение – газы расширяются и совершают полезную работу.
В т.4 открывается выхлопной клапан и давление в цилиндре падает почти до наружного давления.
4-0 – линия выхлопа. При дальнейшем движении поршня справа налево из цилиндра удаляются продукты сгорания через выхлопной клапан при давлении несколько превышающем атмосферное.
Рабочий процесс реального двигателя совершается за четыре хода поршня – такта или за два оборота вала. Такие ДВС наз. четырехтактными.
Цикл реального ДВС не является замкнутым и состоит из необратимых процессов, т.к. имеют место:
¾ Трение;
¾ Химические реакции в рабочем теле;
¾ Конечные значения скоростей поршня;
¾ Теплообмен при конечной разности температур, и т.д.
Анализ такого цикла с точки зрения теории тепловых процессов невозможен.
Поэтому термодинамика исследует идеальные циклы ДВС, состоящие из обратимых процессов.
Допущения при исследованиях:
1. Рабочее тело – идеальный газ с постоянной теплоемкостью;
2. Цилиндр заполнен постоянным количеством рабочего тела;
3. Подвод теплоты к рабочему телу осуществляется не за счет сжигания топлива, а от внешних источников;
4. Разность температур между источником теплоты и рабочим телом - бесконечно мала;
5. Разность температур между приемником теплоты и рабочим телом - бесконечно мала;
Изучение идеальных термодинамических циклов позволяет производить при принятых допущениях анализ и сравнение работы различных ДВС, их экономичность.
|
|
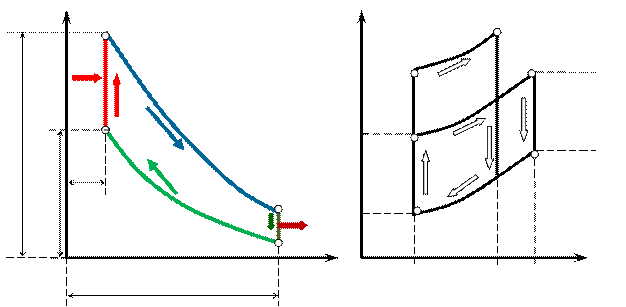
Рис. 2.2 Идеальный цикл ДВС с подводом теплоты в процессе  в pv- TS-координатах
в pv- TS-координатах
Рассмотрим идеальный термодинамический цикл, состоящий из двух изохор и двух адиабат.
Идеальный газ с начальными параметрами p 1, v 1, и T 1 сжимается по адиабате 1-2 то т.2.
По изохоре 2-3 рабочему телу сообщается количество теплоты q 1.
Рабочее тело расширяется по адиабате 3-4.
По изохоре 4-1 рабочее тело возвращается в первоначальное состояние и при этом отводится теплота q 2 в теплоприемник.
Характеристиками цикла являются: степень сжатия 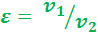 и степень повышения давления
и степень повышения давления 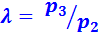 .
.
Определяем термический КПД цикла, считая, что изохорная теплоемкость 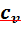 и величина k постоянны:
и величина k постоянны:
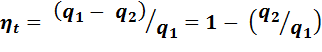
Количество подведенной теплоты:
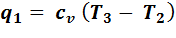 ,
,
Количество отведенной теплоты:
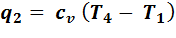
Тогда термический КПД цикла:
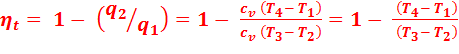 (2.4)
(2.4)
Параметры рабочего тела во всех характерных точках цикла:
В точке 2:
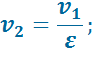
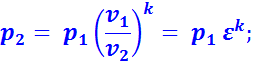
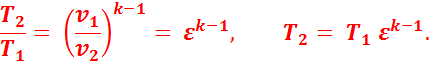
В точке 3:
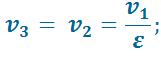
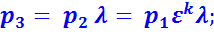
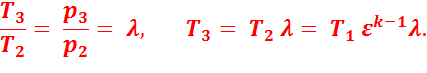
В точке 4:
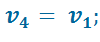
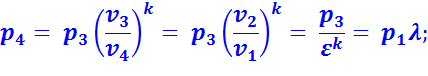
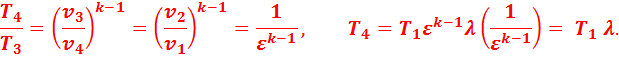
Подставив найденные значения температур в уравнение (2.4), получим:
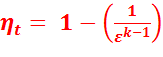 (2.5)
(2.5)
Из уравнения (2.5) следует, что термический КПД такого цикла зависит от степени сжатия 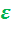 и показателя адиабаты k, т.е. от природы рабочего тела. От степени повышения давления
и показателя адиабаты k, т.е. от природы рабочего тела. От степени повышения давления 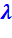 КПД этого цикла не зависит.
КПД этого цикла не зависит.
В таблице 2.1 приведены величины термического КПД цикла с быстрым сгоранием топлива при  при различных значениях
при различных значениях 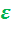 и k.
и k.
Таблица 2.1
|
|
| |
| k = 1,35 | k = 1,4 | |
| 3 | 32,0 | 36,0 |
| 4 | 38,0 | 43,0 |
| 5 | 42,5 | 47,5 |
| 6 | 46,5 | 51,5 |
| 7 | 49,4 | 55,0 |
| 8 | 51,7 | 57,0 |
| 10 | 55,2 | 61,5 |
По TS-диаграмме КПД определим из соотношения площадей:
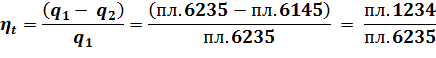
При равенстве количеств теплоты, подведенных в двух циклах, пл. 67810 = пл. 6235, но при разных степенях сжатия КПД будет больше у цикла с большей степенью сжатия, т.к. в теплоприемник отводится меньшее количество теплоты:
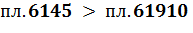
Увеличение степени сжатия ограничивается опасностью преждевременного воспламенения смеси, а также высокой скорости сгорания, что может вызвать детонацию (взрывное горение).
Для каждого топлива должна применяться оптимальная степень сжатия. В зависимости от вида топлива степень сжатия в этих двигателях:
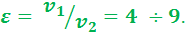
КПД двигателей с подводом теплоты при 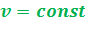 невысок.
невысок.
Теоретическая полезная работа 1 кг рабочего тела:
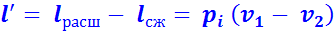 (2.6)
(2.6)
Величину 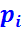 наз. средним индикаторным давлением. Это условное постоянное давление под действием которого поршень в течение одного хода совершает работу, равную работе всего цикла.
наз. средним индикаторным давлением. Это условное постоянное давление под действием которого поршень в течение одного хода совершает работу, равную работе всего цикла.
Для цикла с подводом теплоты при  среднее индикаторное давление:
среднее индикаторное давление:
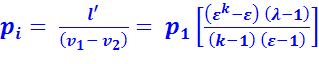 (2.7)
(2.7)
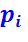 возрастает с увеличением:
возрастает с увеличением: 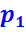 ;
; 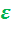 ;
; 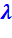 .
.
Теоретическая полезная работа 1 кг рабочего тела также:
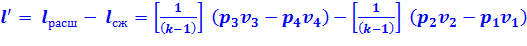 (2.8)
(2.8)
2.3 Цикл с подводом теплоты в процессе 
Исследование циклов с подводом теплоты при  показало, что для повышения экономичности таких двигателей необходимо применять высокие степени сжатия.
показало, что для повышения экономичности таких двигателей необходимо применять высокие степени сжатия.
Степень сжатия ограничивается температурой самовоспламенения горючей смеси.
Если произвести раздельное сжатие воздуха и топлива – это ограничение отпадает.
Воздух при большом сжатии имеет настолько высокую температуру, что подаваемое в цилиндр топливо самовоспламеняется без всяких запальных приспособлений.
Раздельное сжатие воздуха и топлива позволяет использовать любое жидкое тяжелое и дешовое топливо – мазут, нефть, смолы, каменноугольные масла.
Такое раздельное сжатие воздуха и топлива осуществляется в двигателях, работающих с постепенным сгоранием топлива при постоянном давлении.
Воздух сжимается в цилиндре двигателя, а жидкое топливо распыляется сжатым воздухом от компрессора.
Раздельное сжатие позволяет применять высокие степени сжатия: (до 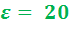 ) и исключает преждевременное самовоспламенение топлива.
) и исключает преждевременное самовоспламенение топлива.
Процесс горения топлива при постоянном давлении обеспечивается регулировкой топливной форсунки ( ДВС Дизеля).
Рассмотрим идеальный цикл ДВС с постепенным сгоранием топлива при постоянном давлении и с подводом теплоты при  .
.
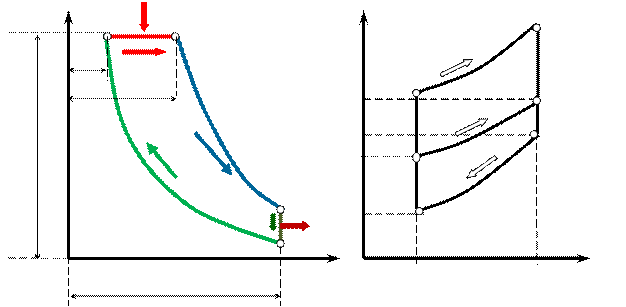
Рис. 2.3 Идеальный цикл ДВС с подводом теплоты в процессе  в pv- TS-координатах
в pv- TS-координатах
Идеальный газ с начальными параметрами p 1, v 1, и T 1 сжимается по адиабате 1-2 то т.2.
По изобаре 2-3 рабочему телу сообщается количество теплоты q 1.
От т.3 рабочее тело расширяется по адиабате 3-4.
По изохоре 4-1 рабочее тело возвращается в первоначальное состояние и при этом отводится теплота q 2 в теплоприемник.
Характеристиками цикла являются: степень сжатия 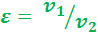 и степень предварительного расширения
и степень предварительного расширения 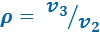 .
.
Определяем термический КПД цикла, считая, что теплоемкости 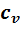 и
и 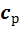 , а также величина k =
, а также величина k = 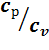 постоянны:
постоянны:
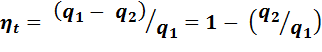
Количество подведенной теплоты:
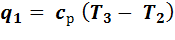 ,
,
Количество отведенной теплоты:
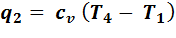
Тогда термический КПД цикла:
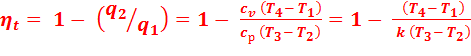 (2.8)
(2.8)
Параметры рабочего тела во всех характерных точках цикла:
В точке 2:
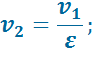
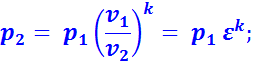
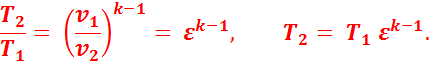
В точке 3:
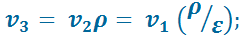
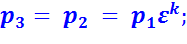
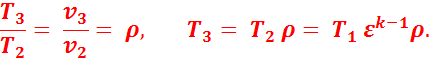
В точке 4:
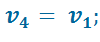
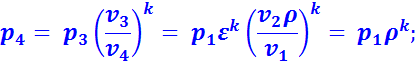
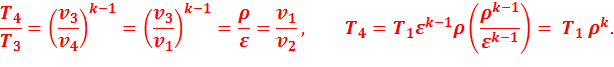
Подставив найденные значения температур в уравнение (2.8), получим:
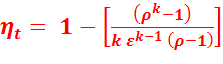 (2.9)
(2.9)
Из уравнения (2.9) следует, что термический КПД такого цикла зависит от степени сжатия 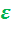 , показателя адиабаты k, т.е. от природы рабочего тела и степени предварительного расширения
, показателя адиабаты k, т.е. от природы рабочего тела и степени предварительного расширения 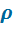 . С увеличением
. С увеличением 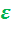 и k – КПД этого цикла увеличивается, а с увеличением
и k – КПД этого цикла увеличивается, а с увеличением 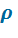 – уменьшается.
– уменьшается.
В таблице 2.2 приведены величины термического КПД цикла с подводом теплоты при  при различных значениях
при различных значениях 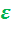 и
и 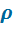 при k = 1,35.
при k = 1,35.
Таблица 2.2
|
|
|
|
| |
При 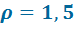
| При 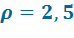
| |||
| 10 | 52,0 | 46,0 | - | - |
| 12 | 54,0 | 49,0 | 25,7 | 907 |
| 14 | 57,0 | 52,0 | 31,8 | 956 |
| 16 | 59,0 | 54,0 | 41,4 | 1020 |
| 18 | 61,9 | 56,7 | - | - |
| 20 | 63,0 | 56,0 | - | - |
По TS-диаграмме КПД определим из соотношения площадей:
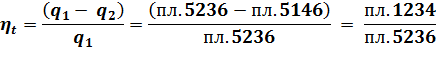
При равенстве площадей отведенной теплоты в теплоприемник (пл.5146), КПД будет больше у цикла с большей степенью сжатия, т.к. площадь его полезной работы будет больше:
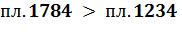
Для цикла с подводом теплоты при  среднее индикаторное давление:
среднее индикаторное давление:
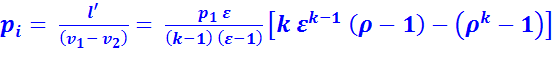 (2.10)
(2.10)
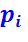 возрастает с увеличением:
возрастает с увеличением: 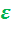 и
и 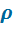 .
.
Теоретическая полезная работа 1 кг рабочего тела за один цикл:
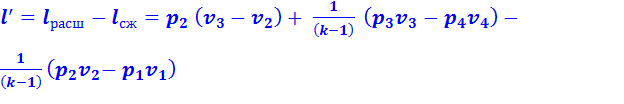 (2.11)
(2.11)
2.4 Цикл с подводом теплоты в процессе при  и
и  , или цикл со смешанным подводом теплоты
, или цикл со смешанным подводом теплоты
Двигатели с постепенным сгоранием топлива при  имеют ряд недостатков:
имеют ряд недостатков:
§ На работу компрессора (для подачи топлива) расходуется 6 – 10% мощности двигателя;
§ Наличие компрессора усложняет конструкцию и уменьшает экономичность работы двигателя;
§ Сложные устройства насоса и форсунки;
§ Установка имеет значительнеый вес.
Г.В. Тринклер создал бескомпрессорный двигатель высокого сжатия с механическим распылением топлива при давлениях 500-700 бар, лишенный недостатков обоих приведенных типов двигателей.
Жидкое топливо топливным насосом подается через топливную форсунку в головку цилиндра (или в специальную предкамеру) в виде мельчайших капелек.
Попадая в нагретый воздух, топливо самовоспламеняется и горит в течение всего периода, пока открыта форсунка: вначале при  , а затем при
, а затем при  .
.
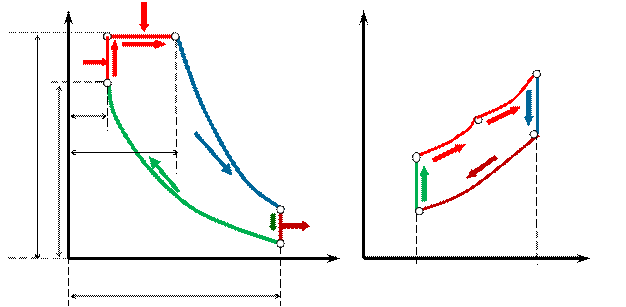
Рис. 2.4 Идеальный цикл ДВС с подводом теплоты в процессе при  и
и  в pv- TS-координатах
в pv- TS-координатах
Идеальный газ с начальными параметрами p 1, v 1, и T 1 сжимается по адиабате 1-2 то т.2.
По изохоре 2-3 рабочему телу сообщается первая доля теплоты q 1 ′.
По изобаре 3-4 подводится вторая доля теплоты q 1 ′′.
От т.4 рабочее тело расширяется по адиабате 4-5.
По изохоре 5-1 рабочее тело возвращается в первоначальное состояние в т.1 и при этом отводится теплота q 2 в теплоприемник.
Характеристиками цикла являются: степень сжатия 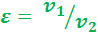 , степень повышения давления
, степень повышения давления 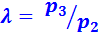 и степень предварительного расширения
и степень предварительного расширения 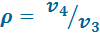 .
.
Определяем термический КПД цикла, считая, что теплоемкости 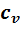 и
и 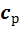 , а также величина k =
, а также величина k = 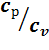 постоянны:
постоянны:
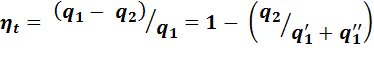
Первая доля подведенной теплоты:
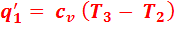 ,
,
Вторая доля подведенной теплоты:
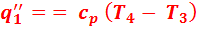
Количество отведенной теплоты:
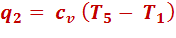
Тогда термический КПД цикла:
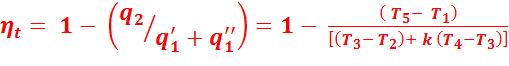 (2.12)
(2.12)
Параметры рабочего тела во всех характерных точках цикла:
В точке 2:
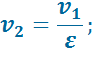
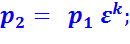
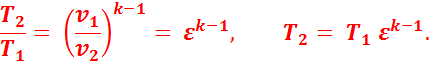
В точке 3:
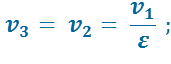
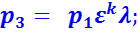
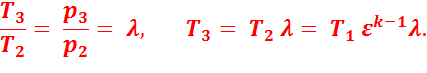
В точке 4:
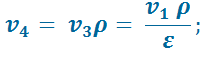
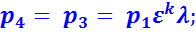
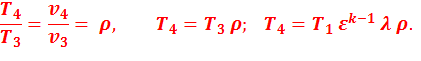
В точке 5:
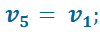
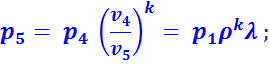
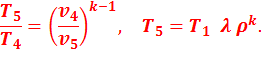
Подставив найденные значения температур в уравнение (2.13), получим:
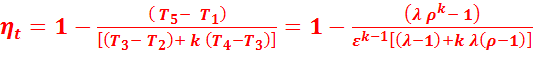 (2.14)
(2.14)
Из уравнения (2.14) следует, что термический КПД такого цикла зависит от степени сжатия 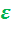 , степени повышения давления
, степени повышения давления 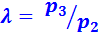 , степени предварительного расширения
, степени предварительного расширения 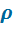 и показателя адиабаты k, т.е. от природы рабочего тела.
и показателя адиабаты k, т.е. от природы рабочего тела.
С увеличением 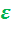 ,
, 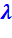 и k – КПД этого цикла увеличивается, а с увеличением
и k – КПД этого цикла увеличивается, а с увеличением 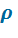 – уменьшается.
– уменьшается.
По TS-диаграмме КПД определим из соотношения площадей:
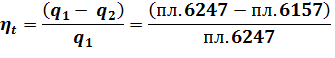
Для этих двигателей обычно принимают:
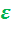 = 10 – 14;
= 10 – 14;
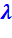 = 1,2 – 1,7;
= 1,2 – 1,7;
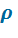 = 1,1 – 1,5;
= 1,1 – 1,5;
Теоретическая полезная работа 1 кг рабочего тела за один цикл:
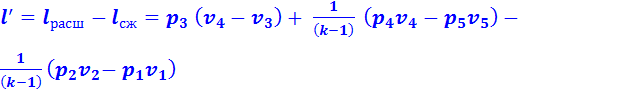 (2.15)
(2.15)
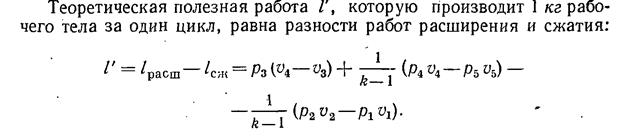
Для цикла со смешанным подводом теплоты среднее индикаторное давление:
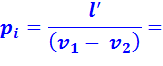
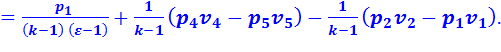 (2.16)
(2.16)
ТДЭФФ-3
ЦИКЛЫ ГАЗОТУРБИННЫХ УСТАНОВОК
Общие сведения
Основными недостатками поршневых ДВС являются:
§ ограниченность их мощности;
§ невозможность адиабатного расширения рабочего тела до атмосферного давления.
Эти недостатки отсутствуют в ГТУ. В них рабочее тело – продукты сгорания жидкого или газообразного топлива, имеющие высокие температуру и давление, из камеры сгорания направляются в сопло, в котором расширяются и с большой скоростью поступают на лопатки газовой турбины, где их кинетическая энергия превращается в механическую работу.
Преимущества ГТУ перед ДВС:
§ Относительно малый вес и небольшие габариты;
§ В ГТУ нет деталей с возвратно-поступательным движением;
§ ГТУ могут выполняться с более высокими числами оборотов и большими единичными мощностями.
При создании крупных стационарных ГТУ возникает ряд проблем:
Методы повышения эффективности (КПД) ГТУ
Известно, что термический КПД ГТУ растет с увеличением степени повышения давлений 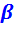 .
.
Однако с ростом 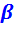 увеличивается и температура газов в конце сгорания топлива
увеличивается и температура газов в конце сгорания топлива 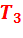 , в результате чего быстро разрушаются лопатки турбин и сопловые аппараты, охлаждение которых затруднительно.
, в результате чего быстро разрушаются лопатки турбин и сопловые аппараты, охлаждение которых затруднительно.
Чтобы увеличить КПД ГТУ применяют:
1. Регенерацию теплоты газов вышедших из камеры сгорания на подогрев сжатого воздуха из турбокомпрессора, который из регенератора подогретый поступает в камеру сгорания.
2. Многоступенчатое сжатие воздуха в компрессоре.
3. Многоступенчатое сгорание.
Известно, что наиболее термодинамически эффективными в циклах тепловых машин являются изотермные процессы сжатия и подвода теплоты.
Для приближения действительного процесса сжатия к изотермному в компрессорах применяют многоступенчатое сжатие с промежуточным охлаждением.
В газовых турбинах для приближения действительного процесса подвода теплоты к изотермному применяют ступенчатое сгорание с расширением продуктов сгорания в отдельных ступенях турбины.
Чем больше число ступеней расширения и сжатия, тем выше термический КПД ГТУ.
Но применение большого числа камер сгорания и холодильников в установке нецелесообразно т.к.:
§ Значительно усложняется и удорожается конструкция;
§ Увеличиваются потери от необратимости процессов (снижается эксергетический КПД).
Обычно из технико-экономических соображений ГТУ выполняют с двухступенчатым расширением (сгоранием) и трехступенчатым сжатием воздуха в компрессоре.
ТДЭФФ-4
ЦИКЛЫ ПАРОТУРБИННЫХ УСТАНОВОК
Цикл Ренкина
Основным циклом ПСУ является цикл Ренкина.
В этом цикле осуществляется полная конденсация пара, поэтому вместо громоздкого малоэффективного компрессора для подачи воды в котел применяют питательный насос.
Кроме того, применение перегретого пара в цикле Ренкина позволяет повысить среднеинтегральную температуру подвода теплоты, следовательно, повысить термический КПД цикла.







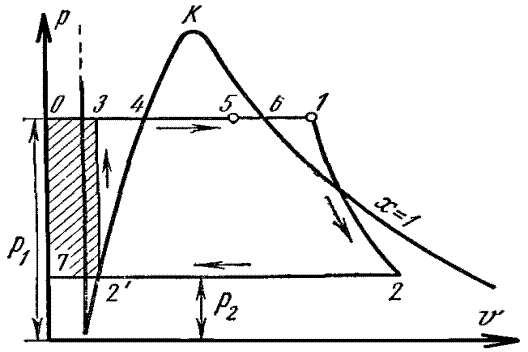
Рис. 4.4 Идеальный цикл Ренкина в pv-диаграмме
Т. 4 – состояние кипящей воды в котле при давлении р1;
Процесс 4-5 – парообразование в котле;
Процесс 5-6 – пар подсушивается в перегревателе;
Процесс 6-1 – перегрев пара в перегревателе при давлении р1;
Процесс 1-2 – полученный пар расширяется по адиабате в цилиндре парового двигателя до давления р2 в конденсаторе;
Процесс 2-2′ – пар полностью конденсируется при давлении р2, отдавая теплоту парообразования охлаждающей воде;
Процесс 2′-3 – процесс сжатия воды в насосе (до 30-40 бар и повышение температуры при этом ничтожно мало). Работа насоса – заштрихованная пл. 032′7.
Полезная работа пара – пл. 2′34612 2′.


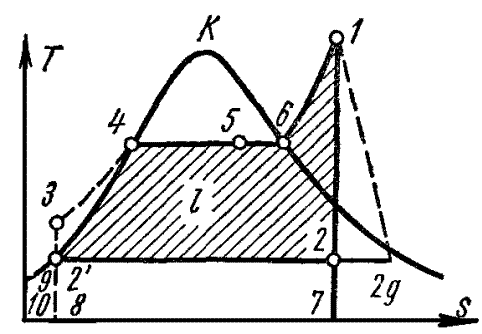
Рис. 4.4 Идеальный цикл Ренкина на TS-диаграмме
Энтальпия пара при выходе из пароперегревателя равна 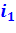 и на TS-диаграмме равна пл. 9 2′ 34617109.
и на TS-диаграмме равна пл. 9 2′ 34617109.
Энтальпия пара на входе в конденсатор 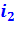 – на TS-диаграмме изображается пл. 92′27109.
– на TS-диаграмме изображается пл. 92′27109.
Энтальпия воды в т. 2′ при выходе из конденсатора 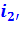 – наTS-диаграмме изображается пл. 92′8109 .
– наTS-диаграмме изображается пл. 92′8109 .
Процесс адиабатного сжатия в насосе на TS-диаграмме изображается адиабатой 2′-3.
Нагрев воды в котле при давлении р1 на TS-диаграмме – изобара 3-4.
Термический КПД цикла Ренкина:
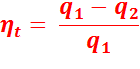
Теплота 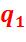 в цикле подводится при p = const в процессах:
в цикле подводится при p = const в процессах:
3-4 – подогрев воды до температуры насыщения (кипения).
4-6 – парообразование,
6-1 – перегрев пара.
Для 1 кг пара 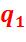 равно разности энтальпий конечной (
равно разности энтальпий конечной ( 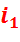 ) и начальной (
) и начальной ( 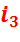 ) точек процесса:
) точек процесса:
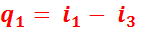
на TS-диаграмме 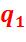 изображается пл. 82′346178.
изображается пл. 82′346178.
Отвод теплоты 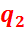 осуществляется в конденсаторе по изобаре 2-2′:
осуществляется в конденсаторе по изобаре 2-2′:
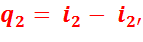
на TS-диаграмме 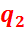 изображается пл. 2′2782′.
изображается пл. 2′2782′.
Тогда:
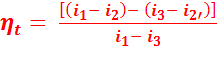 (4.2)
(4.2)
Термический КПД цикла Ренкина также по уравнению:
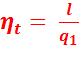 (4.3)
(4.3)
Где 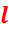 – полезная работа цикла.
– полезная работа цикла.
Полезная работа цикла равна работе паровой турбины минус работа, затраченная на привод насоса.
Работа паровой турбины равна уменьшению энтальпии в процессе 1-2:
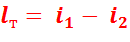
Работа, затраченная на привод насоса при адиабатном сжатии воды в 2′-3:
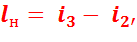
Тогда:
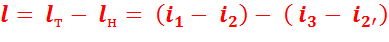
Подставив значение 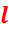 в уравнение (4.3) получим ур-ие (4.2):
в уравнение (4.3) получим ур-ие (4.2):
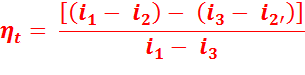
При адиабатном сжатии воды в насосе, с учетом того, что вода практически несжимаема, можно считать этот процесс изохорным, т.е. при v = const, тогда:
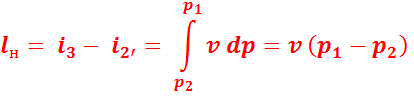
Где 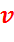 – удельный объем воды при
– удельный объем воды при 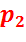 .
.
Заменив в уравнении (4.2) разность 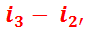 на
на 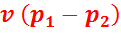 и, проведя преобразования получим уравнение термического КПД цикла Ренкина, применяемое в технических расчетах:
и, проведя преобразования получим уравнение термического КПД цикла Ренкина, применяемое в технических расчетах:
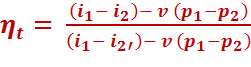 (4.4)
(4.4)
Для практических расчетов (при невысоких давлениях) принимают следующие допущения:
1) Не учитывают повышения температуры при адиабатном сжатии в насосе – точки 2′ и 3 на ТS-диаграмме сливаются;
2) Полагают, что изобары жидкости сливаются с пограничной кривой жидкости (х=0);
С учетом этих допущений цикл Ренкина в pv-координах примет вид:





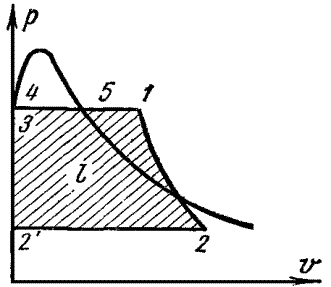
Рис. 17.5 Идеальный цикл Ренкина на pv-диаграмме
А термический КПД цикла определится по приближенной формуле:
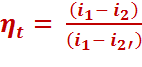 (4.5)
(4.5)
Вычисляется по is-диаграмме.
При расчетах ПСУ определяют теоретический массовый удельный расход пара в кг на 1 МДж:
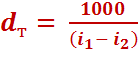 (4.6)
(4.6)
Потери от необратимого расширения пара в турбине учитывают внутренним относительным КПД турбины:
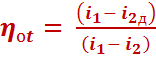 (4.7)
(4.7)
Где - энтальпия в конце действительного расширения пара в турбине.
Потери от необратимости, уменьшая полезную работу, увеличивают удельный расход пара и действительный расход пара:
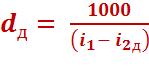 (4.8)
(4.8)
Регенеративный цикл ПСУ
Термический КПД цикла можно значительно повысить введением регенерации теплоты.
Условный предельно-регенеративный цикл ПСУ на рис. 4.9
Подогрев питательной воды (процесс 4-5) производится за счет отведенной теплоты в процессе 2-3.
При этом количество теплоты, отведенное в процессе 2-3 и измеряемое пл. 27832, равно количеству теплоты, подводимому в процессе 4-5 – пл. 04590.
В регенеративном цикле средняя температура подвода теплоты от внешнего источника к рабочему телу получается выше, чем у обычного цикла Ренкина, поэтому регенеративный цикл имеет больший КПД, чем цикл Ренкина, но меньший, чем цикл Карно в таком же интервале температур.
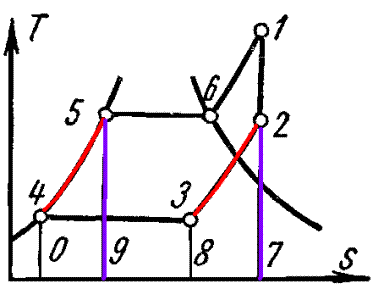
Рис. 4.9 Условный предельно-регенеративный цикл ПСУ
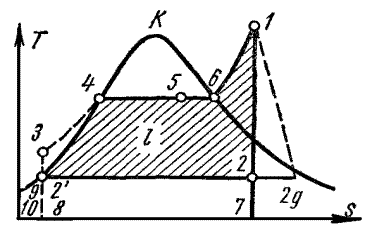
Рис. 4.10 Цикл Ренкина (идеальный)
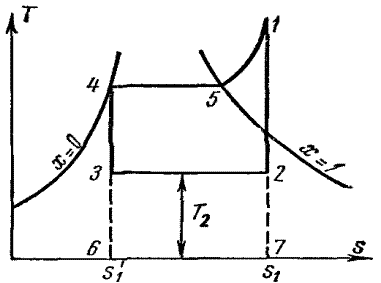
Рис. 4.11 Цикл эквивалентный по термическому КПД предельно-регенеративному циклу ПСУ
Из анализа цикла на на рис. 4.9 следует, что использованная теплота на участке 2-3 для подогрева воды в процессе 4-5 уменьшает удельную полезную работу пара по сравнению с обычным циклом (см. рис. 4.10), т.е. регенеративный цикл характеризуется большим удельным расходом пара.
Ввиду равенства площадей под кривыми процессов 2-3 и 4-5 цикл на рис.4.9 можно заменить эквивалентным по термическому КПД циклом – рис.4.11.
Термический КПД эквивалентного цикла:
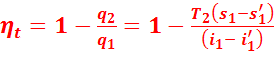 (4.9)
(4.9)
Где 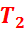 – абсолютная температура пара в конденсаторе;
– абсолютная температура пара в конденсаторе;
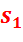 – энтропия перегретого пара;
– энтропия перегретого пара;
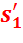 – энтропия кипящей жидкости;
– энтропия кипящей жидкости;
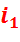 – энтальпия перегретого пара;
– энтальпия перегретого пара;
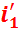 – энтальпия кипящей жидкости при начальном давлении
– энтальпия кипящей жидкости при начальном давлении 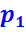 .
.
На практике регенеративный подогрев питательной воды осуществляется в нескольких последовательно вклбченных подогревателях, в каждый из которых поступает небольшое количество пара, отбираемого из соответствующей ступени турбины (такой реальный цикл невозможно изобразить на Ts-диаграмме).
В зависимости от способа включения греющего пара и конденсата в общую сеть питательной воды возможны различные схемы регенерации, отличающиеся по эксплуатационным и экономическим характеристикам.
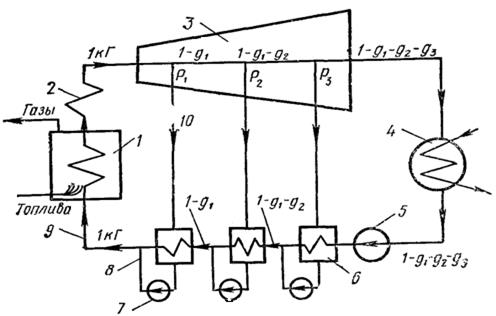
Рис.4.12
На рис 4.12 – каскадная схема паротурбинной установки с тремя отботами пара для подогрева питательной воды.
1 – паровой котел;
2 – пароперегреватель;
3 – паровая турбина;
4 – конденсатор;
5 – насос питательной воды;
6 – поверхностный подогреватель;
7 – дренажный насос;
8 – конденсат греющего пара;
9 – питательная вода;
10 – греющий пар из отбора турбины.
Поступающий из котла пар в турбину 3 имеет давление 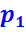 , температуру
, температуру 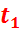 и энтальпию
и энтальпию 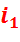 ; в конденсаторе 4 давление
; в конденсаторе 4 давление 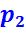 , температура
, температура 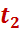 и энтальпия
и энтальпия 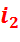 .
.
Через турбину проходит не весь пар. Из каждого килограмма пара, поступающего в турбину, отбирается:
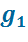 kг в первый подогреватель 6 с энтальпией
kг в первый подогреватель 6 с энтальпией 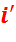 , давлением
, давлением 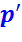 и температурой
и температурой 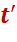 ;
;
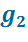 kг во первый подогреватель с энтальпией
kг во первый подогреватель с энтальпией 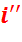 , давлением
, давлением 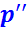 и температурой
и температурой 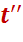 ;
;
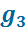 kг в третий подогреватель с энтальпией
kг в третий подогреватель с энтальпией 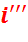 , давлением
, давлением 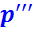 и температурой
и температурой 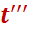 ;
;
Отводится в кондесатор 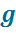 кг пара.
кг пара.
Тогда: 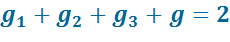
Образовавшийся конденсат
Термодинамическая эффективность теплового оборудования и ТЕПЛОМАССООБМЕННЫХ ПРОЦЕССОВ В НЕМ
ВВЕДЕНИЕ
Весьма обобщенно, задача теплотехника, – создать эффективные способы массового производства и использования энергии различных видов.
Наука - «теплотехника» или область практической деятельности по использованию результатов фундаментальной науки?
Ответ на этот вопрос зависит от того, как мы расшифровываем термин "эффективный способ", от принятых критериев эффективности. Если на первый план выдвигаются экономические критерии, такие как себестоимость произведенной энергии или прибыльность производства, то «теплотехника» есть область предпринимательства в сфере реализации научных знаний.
Если же за критерии брать натуральные показатели, такие как расходы сырья и энергии на получение единичного количества продукта (различных видов энергии) и интенсивность процессов (скорость трансформации вещества и энергии в единичном объеме аппаратуры), то задачи, стоящие перед теплотехником, представляются как сугубо научные: создать такие системы, в которых единичное количество продукта (энергии, транспортируемого вещества) производится из минимального количества сырья, при минимальном потреблении энергии и при максимальной скорости процесса. При этом теплотехник действует в рамках, предопределенных фундаментальными законами природы.
И в этом смысле теплотехника есть часть науки, естественное продолжение или расширение термодинамики и теории тепломассообмена, но с опорой в равной степени и на макроскопическую физику и механику.
Вышесказанное объясняет, почему изучение показателей термодинамической эффективности теплового оборудования и тепломассообменных процессов в нем особенно важно.
Основное внимание в предлагаемом курсе уделяется наиболее "наукоемким" критериям, характеризующим степень термодинамического совершенства теплового оборудования и тепломассообменных процессов в нем.
Выделение этого вопроса продиктовано тем значением для устойчивого развития цивилизации, которое приобретают в современную эпоху проблемы ресурсо- и энергосбережения и снижения антропогенного воздействия на окружающую среду. Выпускниками академии вопросы ресурсо- и энергосбережения должны пониматься не на общегражданском уровне контроля за показаниями счетчиков воды, газа и электричества, а на фундаментальном уровне второго начала термодинамики, уровне управления процессами генерации энтропии.
Содержание этой части курса неизбежно пересекается с содержанием предшествующего курса – "Техническая термодинамика".
В приложении к проблемам теплогазоснабжения, вентиляции и кондиционирования положения термодинамики предстают перед изучающим предмет в новых "одеждах", а именно, в "потоковом" выражении. Уравнения термодинамики характеризуют теперь изменение состояния не статичной порции вещества, а потока вещества, проходящего через технологическую систему. Аналогичным образом вместо количеств энергии, теплоты или работы, воспринимаемых (отдаваемых) порцией вещества, в термодинамическую модель технологической системы входят потоки теплоты и работы и скорости возникновения энтропии в системе.
Как раз в приложении к задачам технологии такие ключевые абстрактные понятия термодинамики как полезная работа системы и максимальная работа системы приобретают совершенно конкретное и ясное содержание.
Таким же конкретным и ясным содержанием наполняется понятие скорости возникновения энтропии. Центральное уравнение термодинамики неравновесных процессов, выражающее скорость роста энтропии как сумму произведений потоков и движущих сил, позволяет вовлечь весь арсенал макроскопической механики, и физики в дело разработки термодинамически более совершенных технологических систем.
В курсе лекций принята терминология, рекомендованная Комитетом научно-технической терминологии АН СССР, (Термодинамика, Сб. определений, Вып. 103, Изд-во "Наука", М. 1984) и обозначения, рекомендованные (Quantities, Units and Symbols in Physical Chemistry, 2nd Edition, IUPAC, 1993).
ТДЭФФ-1
ТЕРМОДИНАМИЧЕСКИЙ АНАЛИЗ И ЕГО ПРИЛОЖЕНИЕ К ОЦЕНКЕ ЭФФЕКТИВНОСТИ ТЕПЛОТЕХНИЧЕСКОГО ОБОРУДОВАНИЯ
Дата: 2019-02-25, просмотров: 672.
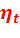
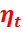
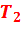 , К
, К