Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

    Для построения сопряжения двух прямых l и m заданным радиусом сопряжения R, предварительно находим центр дуги сопряжения – точку О и точки сопряжения А и В (рис. 19а, б, в).

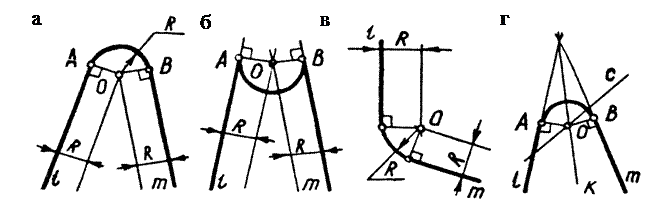
    Точка О найдена как точка пересечения двух прямых, параллельных, соответственно, прямым l и m и расположенных на расстоянии R. Точки сопряжения А и В – основания перпендикуляров, опущенных из точки О.

Рис. 19. Сопряжение прямых

 

    На рис. 19г радиус дуги сопряжения не задан, но на одной прямой (например l) задана точка сопряжения А. Для нахождения центра дуги сопряжения достаточно построить биссектрису угла прямых l и m – прямую k. Величину радиуса сопряжения R найдем, опустив перпендикуляр из точки сопряжения А на биссектрису k. Точка В – вторая точка сопряжения.

     Для построения сопряжение дуги окружности с прямой даны окружности радиуса R₁ (рис. 20), прямые l и радиус сопряжения R. Нахождение центра сопряжения О окружности радиуса R ясно из рисунка.

В задачах (рис. 20в, г, д) даны дуги радиуса R₁, прямые l и точки сопряжения А на них. Необходимо найти вторую точку сопряжения В и радиус сопряжения R.

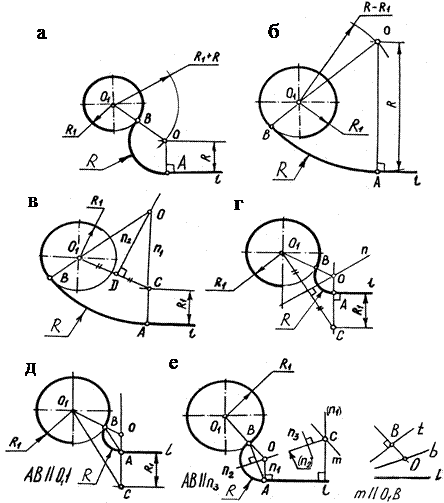Решение задачи (внутреннее сопряжение) (рис. 20в). На перпендикуляре n₁, восстановленном из точки сопряжения А, на расстоянии, равном R_1, находим точку С. Соединив точки С и О₁, строим срединный перпендикуляр n₂ к отрезку О₁С. На пересечении перпендикуляров n ₁ и n ₂ находим центр дуги сопряжения О. Продлив отрезок ОО₁ ,найдем вторую точку сопряжения В.

 

д)                                 е)

Рис. 20. Сопряжение окружности с прямой

 

Задача (рис. 20г) (внешнее сопряжение) решается аналогично задаче на рис. 20в. Другой вариант решения задачи (рис 20г) представлен на  рис. 20д.  Здесь,  построив отрезок  О₁С_, вторую точку сопряжения В находим, проведя прямую АВ !! О₁С. Продлив отрезок О₁В до пересечения  с  перпендикуляром n ₁, находим центр О дуги сопряжения радиуса R.

В задаче (рис. 20е) заданы окружность радиуса R₁ c точкой сопряжения В и прямая l. Для того чтобы найти точку сопряжения А, достаточно знать направление прямой АВ. Для этого на произвольном перпендикуляре n₁ к прямой l возьмем произвольную точку С, через которую проведем прямую m !! О₁В. Биссектриса угла между прямыми m и n₁ – прямая n₂, а перпендикуляр к прямой n₂ – прямая n₃.

а                                             б

в                                                    г

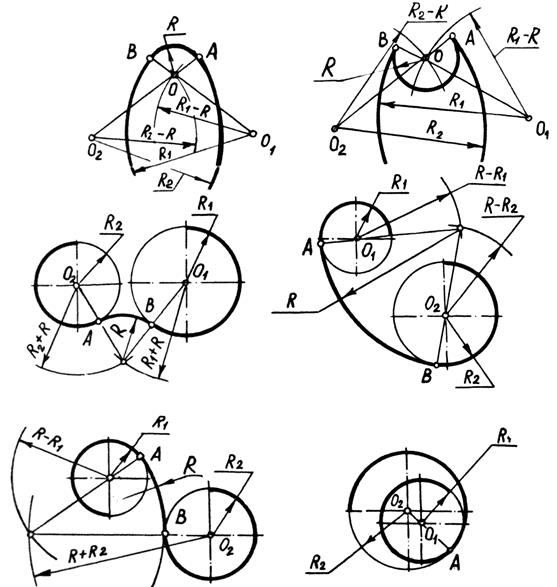Точку  сопряжения А на прямой l находим из условия АВ !! n₃. Далее,  восстановив срединный перпендикуляр n₂ к отрезку АВ, на пересечении  его  с  перпендикуляром  n₁  найдем центр дуги сопряжения О радиуса R. Простейшие случаи сопряжения дуг окружностей представлены на рис. 21. Нахождение центров О дуг сопряжения радиуса R ясно из рис. 21а, б, в, г, д. Точки сопряжения А и В расположены на прямых, соединяющих центры О₁ и О₂ дуг радиусов R₁ и R₂ с центром О дуги сопряжения радиуса R.

д                                                              е

	д                                                     е

 

Рис. 21. Сопряжение дуг окружностей

 

Дуги радиусов R₁ и R₂ (рис. 21е) имеют одну общую точку А, которая и будет точкой сопряжения.

Рассмотренные выше примеры позволяют успешно выполнить графическую работу по теме №1 (рис. 22).

Обозначение R_x показывает, что величина радиуса определяется построением. На чертеже вместо R_x надо поставить соответствующее число со знаком «*», например, R50*, а над основной надписью записать: «Размер для справок».

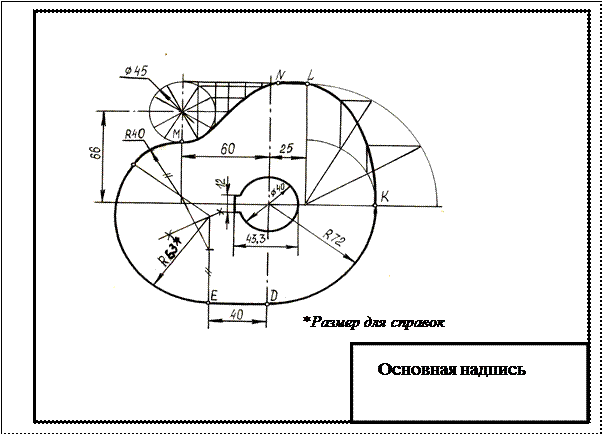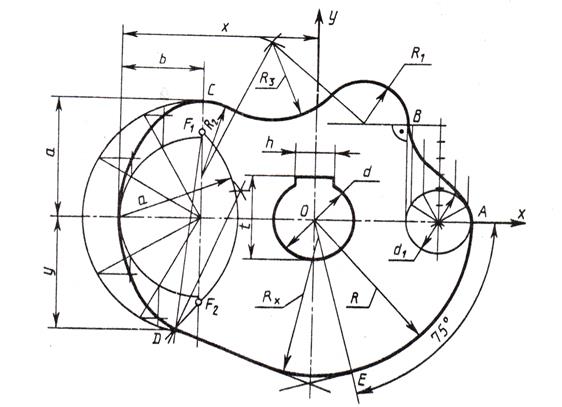
Рис. 22. Пример выполнения чертежа по теме №1

 

Построить очертание кулачка. Данные для своего варианта взять из таблицы I.

    Вопросы для самоконтроля: 1. Сколько форматов А4 содержится в листе формата А1? 2. Как образуются дополнительные форматы чертежей? 3. Чем определяется размер шрифта7 4. Какого начертания и какой толщины проводятся линии обводки видимого контура, линии осевые, центровые, выносные, размерные и невидимого контура? 5. На каком расстоянии от контура рекомендуется проводить размерные линии? 6. В каких случаях стрелку размерной линии заменяют точкой или штрихом? 7. Какие проставляют размеры при выполнении чертежа в масштабе, отличном от 1:1? 8. В каких случаях проставляют знаки ñ, ò, ×,  ?

 

ТАБЛИЦА 1.

Данные для построения кулачка

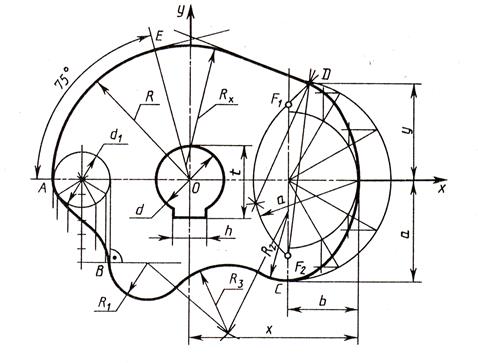
Варианты	R	R1	R2	R3	a	b	d	d1	h	t	x	y
1	115	35	55	35	75	45	40	55	12	45	115	70
11	110	45	50	40	70	40	35	50	10	40	120	60

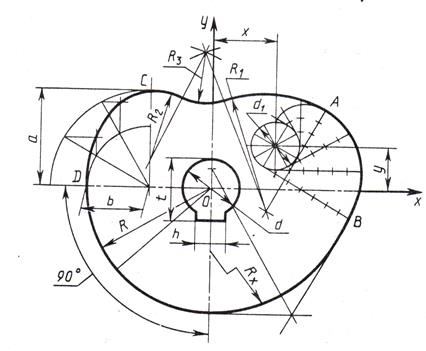
Варианты	R	R1	R2	R3	a	b	d	d1	h	t	x	y
2	120	100	50	30	80	50	45	40	14	50,5	40	35
12	115	110	75	40	90	55	50	45	16	56	45	40

Продолжение табл.1

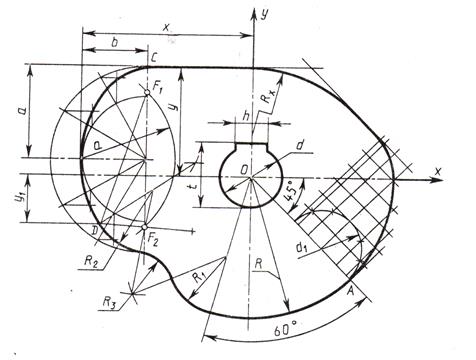
Варианты	R	R1	R2	R3	a	b	d	d1	h	t	x	y
3	95	35	35	25	70	50	40	60	12	45	100	40
13	90	40	40	25	75	45	40	60	12	45	110	35

 

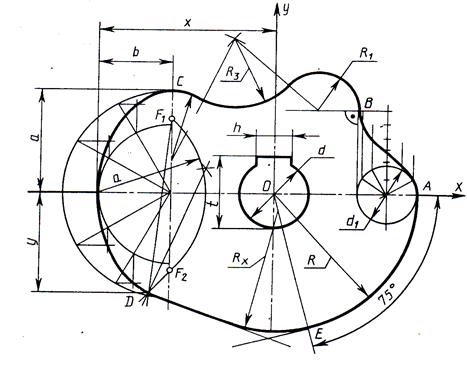
Варианты	R	R1	R2	R3	a	b	d	d1	h	t	x	y
4	115	35	55	35	75	45	40	55	12	45	115	70
14	110	45	50	40	70	40	35	50	10	40	120	60

 

Продолжение табл. 1

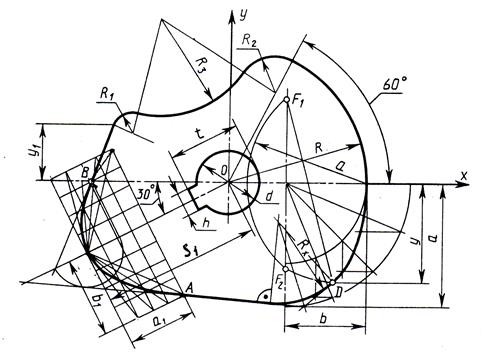
Варианты	S1	a1	b1	R	a	b	y	y1	R1	R2	R3	t	h	d
5	125	52	65	110	100	65	85	45	15	30	80	56	16	50
15	120	50	60	100	90	60	82	40	10	25	75	50,5	14	45

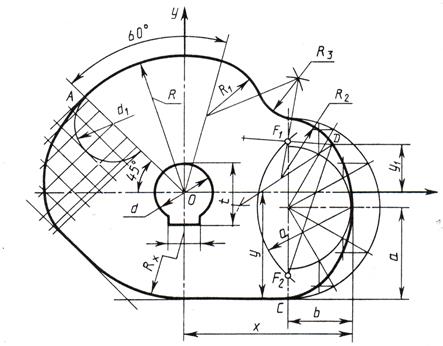
Варианты	R	R1	R2	R3	a	b	d	d1	h	t	x	y1	y
6	95	35	35	25	70	50	40	60	12	45	100	40	85
16	90	40	40	25	75	45	40	60	12	45	100	35	90

Продолжение табл. 1

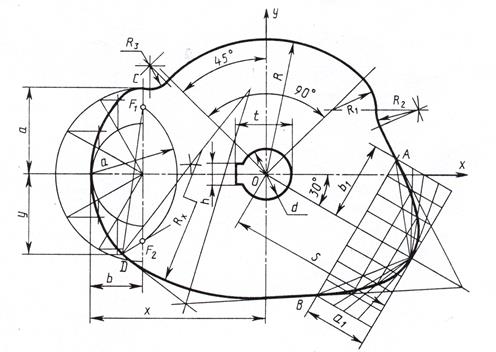
Варианты	R	R1	R2	R3	S	a1	a	b	d	b1	h	t	x	y
7	100	35	30	20	115	45	60	40	45	50	14	50,5	135	54
17	95	50	40	18	120	40	55	45	50	52	16	56	130	45

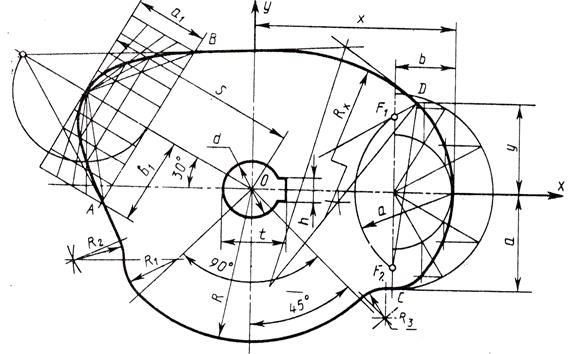
Варианты	R	R1	R2	R3	S	a1	a	b	d	b1	h	t	x	y
8	100	35	30	20	115	45	60	40	45	50	14	50,5	135	54
18	95	50	40	18	120	40	55	35	50	52	16	56	130	45

Продолжение табл. 1

Варианты	R	R1	R2	R3	a	b	d	d1	h	t	x	y
9	115	35	55	35	75	45	40	55	12	45	115	70
10	110	45	50	40	70	40	35	50	10	40	120	60

        

    Для вариантов 3,5–8,13; 15–18 центры радиусов R_x и R₂ лежат на биссектрисе угла F₁DF₂.

Тема №2

Построение трех видов