Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

     Лекальные кривые не могут быть построены с помощью циркуля. Вначале находят ряд точек, принадлежащих данной лекальной кривой. Затем полученные точки плавно соединяют по лекалу.

    При сечении плоскостью прямого кругового конуса, в зависимости от положения плоскости по отношению к оси конуса, получаются контуры сечения, образующие эллипс, параболу, гиперболу.

       Эллипс – замкнутая плоская кривая, сумма расстояний каждой точки которой до двух данных точек (фокусов), лежащих на большой оси, есть величина постоянная и равная длине большой оси.

   Широко применяется в технике способ построения эллипса по большой АВ и малой СD осям (рис. 2).

   Проводим две перпендикулярные осевые линии. Затем от центра О откладываем вверх и вниз по вертикальной оси отрезки, равные длине малой полуоси b, а влево и вправо по горизонтальной оси – отрезки, равные длине большой полуоси a.

Из центра О радиусами ОА и ОС проводим две концентрические окружности и ряд лучей-диаметров. Из точек пересечения лучей с окружностями проводим линии, параллельные осям эллипса, до взаимного пересечения в точках, которые принадлежат эллипсу. Намеченную линию обводим по лекалу.

Точки сопряжения кривых – это точки, в которых сопрягаемые кривые имеют общую касательную. Построение сопряжения кривых в заданных точках сводится к построению касательных в этих точках (рис. 3).

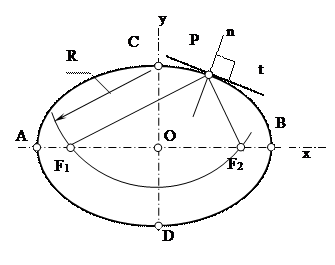АВ и СD – оси эллипса, точка Р– произвольная точка, через которую проводим касательную. С помощью радиуса R=ОА находим фокусы эллипса точки F₁ и F₂ (СF₁ = СF₂ = R = ОА= ОВ). Соединяем точку Р с фокусами F₁ и F₂. Биссектриса угла F₁РF₂ будет нормалью n, к которой и строим касательную t.

 

 

                        

 

             R=OA

             PF₁+PF₂=AB

 

 

             

Рис. 3. Построение касательной к эллипсу в точке Р.

               АВ и СD – оси эллипса, F₁ и F₂ - фокусы

       

Парабола – плоская кривая, каждая точка которой равноудалена от директрисы DD₁ – прямой, перпендикулярной к оси симметрии параболы, и от фокуса F – точки, расположенной на оси симметрии параболы (рис. 4).

    Расстояние КF между директрисой и фокусом называется параметром p параболы. Точка О, лежащая на оси симметрии, называется вершиной параболы и делит параметр p пополам.

    Для построения параболы по заданной величине параметра p проводим ось симметрии параболы вертикально (рис. 4) и откладываем отрезок КF = p. Через точку К перпендикулярно оси симметрии проводим директрису DD₁. Отрезок КF делим пополам и получаем вершину О параболы. От вершины О на оси симметрии отмечаем ряд произвольных точек I –VI c постепенно увеличивающимся расстоянием между ними. Через эти точки проводим вспомогательные прямые, перпендикулярные оси. На вспомогательных прямых из фокуса F делаем засечки радиусом, равным расстоянию от прямой до директрисы. Например, из точки F на вспомогательной прямой, проходящей через точку V, делаем засечку дугой R₁ = KV; полученная точка 5 принадлежит параболе.

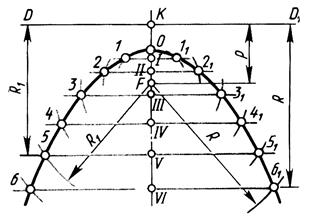Рис. 4. Построение параболы

 

        Если требуется построить параболу по заданной вершине О, оси ОС и точке В (рис. 5), то строим вспомогательный прямоугольник АВСО. Стороны прямоугольника АВ и ОА делим на равные части и точки деления нумеруем. Горизонтальный ряд делений соединяем лучами с вершиной О, а через точки делений, расположенные на АО, проводим прямые линии, параллельные оси параболы. Точки D, E, F, K, L, M, N пересечения горизонтальных прямых 1₁, 2₁, 3₁, … с лучами О1, О2, О3, … принадлежат параболе.

 

 

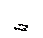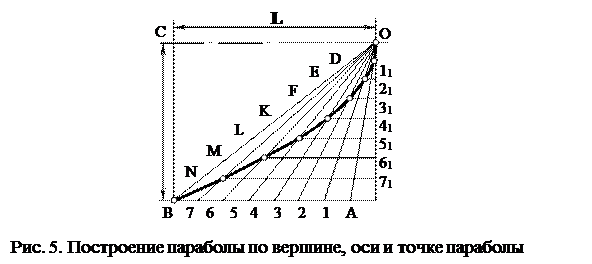Построение касательной в произвольной точке К параболы показано на рис. 6. Точку К соединяем с фокусом F, прямую ЕК проводим перпендикулярно к директрисе у, ЕК=КF. Биссектриса угла ЕКF и будет касательной к параболе в точке К. Точку  К  соединяем с фокусом F. Прямая ЕК  перпендикулярна  к  директрисе  y. Исходя  из свойства  параболы  (см. рис. 4)  ЕК=KF.  Биссектриса  t  угла  ЕКF и будет касательной к параболе в точке К. 

 

 

                     

 

                                                                   

 

 

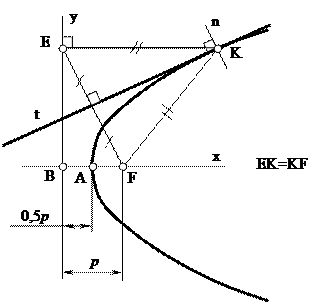
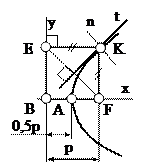
        Рис. 6. Построение касательной к параболе в точке К:

                   х – ось параболы, у – директриса, А – вершина,

                   F – фокус

 

Гипербола – плоская кривая, состоящая из двух разомкнутых, симметрично расположенных ветвей (рис. 7). Разность расстояний от каждой точки гиперболы до фокусов F и F₁ есть величина постоянная и равная расстоянию между вершинами гиперболы А и В.

 

Рис. 7. Построение гиперболы

Рассмотрим построение гиперболы по заданному расстоянию между вершинам А и В и фокусному расстоянию FF₁. Разделив фокусное расстояние FF₁ пополам, получаем точку О, от которой по обе стороны откладываем по половине заданного расстояния между вершинами А и В. Вниз от фокуса F намечаем ряд произвольных точек 1, 2, 3, 4 … с постепенным увеличением расстояния между ними. Из фокуса F описываем дугу вспомогательной окружности радиусом R, равным, например, расстоянию от вершины гиперболы В до точки 3. Из фокуса F₁ проводим вторую дугу вспомогательной окружности радиусом r , равным расстоянию от вершины А до точки 3. На пересечении этих дуг находим точки С и С₁, принадлежащих гиперболе. Таким же способом находим остальные точки гиперболы. Вторую ветвь гиперболы строим аналогичным образом.

Рассмотрим построение гиперболы по известным ее асимптотам* l ₁ и l ₂ и точке Р (рис. 8). Точка О пересечения асимптот l ₁ и l ₂ является центром гиперболы.

Через точку Р проводим прямые m и n, параллельные асимптотам l₁ и l₂, находим точки пересечения произвольных лучей а и b, проведенных из точки О с этими прямыми. Дальнейшие построения на рис. 8 показаны стрелками.

                                                                             

 

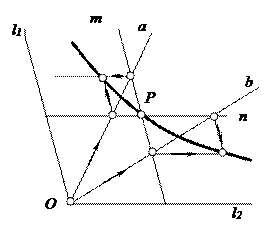Рис. 8. Построение гиперболы по асимптотам l₁ и l₂ и точке Р

 

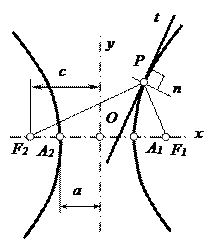
Построение касательной в произвольной точке Р гиперболы показано на рис. 9. Точку Р соединяем с фокусами гиперболы F₁ и F₂. Далее строим биссектрису угла F₁PF₂, которая и будет касательной к гиперболе в точке Р.

Построение касательной к гиперболе, построенной по заданной точке и двум асимптотам p и p ₁, в некоторой точке Р показано на рис. 10. Через точку Р проводим отрезок, параллельный одной из асимптот. В данном случае отрезок Р1 Õp. На другой асимптоте p ₁ откладываем отрезок 1М=01. Прямая t, проведенная через точки М и Р, является касательной к гиперболе.

 

F₁F₂=2c, A₁A₂=2a

F₂P-F₁P=2a

 

Рис. 10. Построение касательной к ветви гиперболы в точке Р:  p , p 1 – асимптоты, О – центр гиперболы

Рис. 9. Построение касательной

  к гиперболе в точке Р:

х – действительная ось;

у – мнимая ось;

О – центр гиперболы;

А_1, А₂ – вершины;

F_1, F₂ – фокусы

 

Синусоида – плоская кривая, выражающая закон изменения синуса угла в зависимости от изменения величины угла (рис. 11).

Величина r называется амплитудой синусоиды, L – длиной волны или периодом синусоиды. (L = 2pr).

Для построения синусоиды проводим горизонтальную ось и на ней откладываем заданную длину волны АВ (рис. 11). Отрезок АВ делим на несколько равных частей, например, на 12. Слева вычерчиваем окружность, радиус которой равен величине амплитуды, и делим ее также на 12 равных частей. Точки деления нумеруем и через них проводим горизонтальные прямые. Из точек деления отрезка АВ восстанавливаем перпендикуляры к оси синусоиды и на их пересечении с горизонтальными прямыми находим точки синусоиды.

Полученные точки синусоиды а₁,  а₂,  а₃, … соединяем по лекалу кривой.

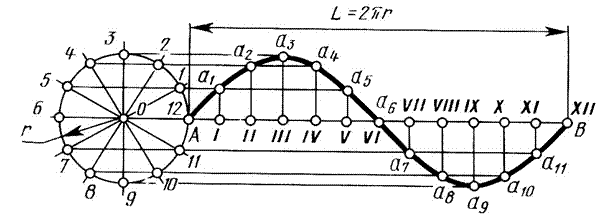
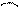Для построения касательной к синусоиде в произвольной точке Р (рис. 12) воспользуемся окружностью, по которой строится синусоида, и найдем точку Р₁ на окружности. Проведя касательную t к окружности в точке Р₁ и найдя на ней точку С (Р₁С=АР₁), строим точку С^'. Прямая С^'Р является касательной к синусоиде.

а)

б)

Рис. 11. Построение синусоиды

 

Рис. 12. Построение касательной к синусоиде

 

Спираль Архимеда (рис. 13) очерчивается точкой А при поступательном равномерном перемещении ее по прямой l при одновременном равномерном вращении последней. Величина поступательного перемещения точки за один оборот прямой l – шаг спирали Архимеда – а=О8.

Для построения касательной к спирали Архимеда в произвольной точке Р (рис. 14) необходимо построить вспомогательную окружность с центром в точке О и диаметром d = а/p = ОА/p. Из центра О вспомогательной окружности проводим прямую ОР и перпендикулярно к ней – радиус ОМ. Перпендикуляр к отрезку МР есть касательная t к спирали Архимеда в точке Р.

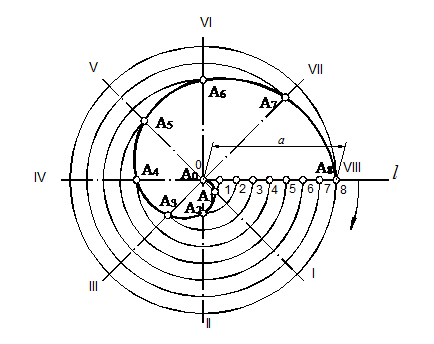
Рис. 13. Построение спирали Архимеда

 

                   

 

Рис. 14. Построение касательной к спирали Архимеда

 

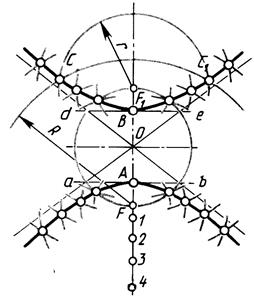
Циклоида (греч. кyкloeides – кругообразный ) – траектория точки производящей окружности диаметра d, перекатывающейся без скольжения по прямой линии.

Построение циклоиды по двум точкам сопряжения А и А₄ и известному диаметру производящей окружности d показано на рис. 15. Точка производящей окружности А после перекатывания по оси х окружности на расстоянии А-1 (длина отрезка равна длине дуги А-1) поднимется на высоту h. Проводим отрезок А₁1 Õx и отрезок А₁1¢Õ А1. Точка А₁ принадлежит циклоиде и т.д.

 

 

 

Рис. 15. Построение циклоиды:

 d –диаметр производящей окружности,

                            R – радиус

 

На рис. 16  показано построение касательной к циклоиде в произвольной точке Р. Воспользовавшись радиусом производящей окружности R=ОС и линией центров этих окружностей, находим центр окружности в положении, когда на ней находится точка Р – точку О₁. Нижнюю точку М вертикального диаметра производящей окружности в рассматриваемом положении соединяем с точкой Р. Прямая МР – нормаль к циклоиде в точке Р. Касательная t перпендикулярна к нормали n.  

Эвольвента (лат. evolvens – развернутая) – плоская кривая, являющаяся разверткой другой кривой – эволюты (лат. evoluta – развертываемая). Касательные к эволюте являются нормалями к эвольвенте (рис. 17) или прямыми огибающими эволюту.

Построение эвольвенты окружности по основной окружности диаметра d _b показано на рис. 17. Эвольвента описывается в пространстве точкой О прямой l при перекатывании последней по окружности диаметра d _b или точкой О нити, «разматываемой» с окружности диаметра d _b (натяжение нити на рис. 17  показано стрелками).

 

 

 

 

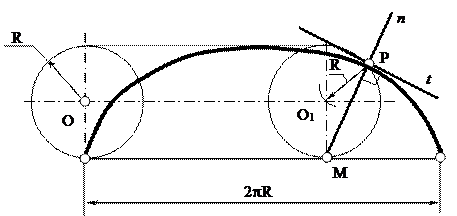Рис. 16. Построение касательной к циклоиде

                           R – радиус производящей окружности

 

 

Рис. 17. Построение эвольвенты окружности диаметра d_b:

d_b - основная окружность (эволюта), О – точка заострения эвольвенты

 

Произвольная точка эвольвенты С построена на прямой, касающейся основной окружности в точке D из условия что длина отрезка DС равна длине дуги основной окружности ОD.

Для построения касательной к эвольвенте в произвольной точке Р строим касательную Р–8 окружности (рис. 18). Перпендикуляр к Р–8 есть касательная t к эвольвенте.

 

 

 

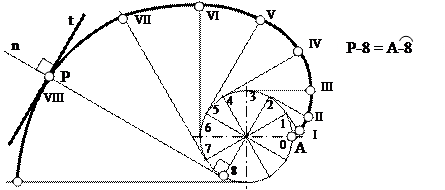
Рис. 18. Построение касательной к эвольвенте