1. Работа по учебнику.

Задание № 15 (с. 71).

Выполняя это задание, учащиеся должны разобраться в терминологии, связанной с направлением движения двух объектов. В дальнейшем это пригодится при решении задач на движение.

Целесообразно решить задачу наглядно, используя модели машинок.

Учитель просит одного из учеников расположить на магнитной доске (фланелеграфе) модели машинок так, чтобы они двигались навстречу друг другу.

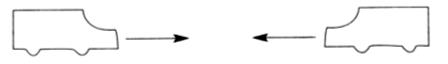
Затем спрашивает: «Верно ли, что машины едут в противоположных направлениях?» Одни будут говорить, что верно, а другие – что неверно. Двигая модели машин навстречу друг другу, продемонстрируйте детям, что машины двигаются в противоположных направлениях.

Делаем вывод: когда машины едут навстречу друг другу, они двигаются в противоположных направлениях. Далее попросите расположить модели машин так, чтобы они двигались в одном направлении (одну из машин надо развернуть).

И, наконец, попросите учащихся расположить модели так, чтобы машины двигались в разных направлениях. Например, так:

Можно предложить дополнительные задания. В каких направлениях двигаются машины?

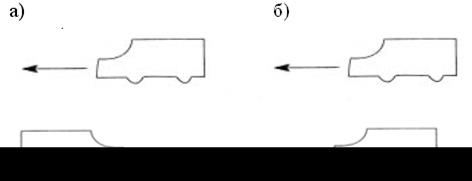
(В противоположных           (В одном направлении.)

   направлениях.)

в)

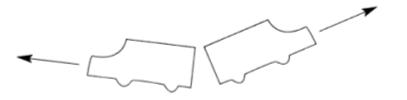
(В разных направлениях.)

Задание № 16 (с. 72).

– Рассмотрите иллюстрацию и прочитайте задачу.

– Что известно в задаче? Что требуется узнать?

Повторить условие задачи и наметить план ее решения лучше всего с опорой на иллюстрацию в учебнике. Рассуждать учащиеся должны примерно так:

«Известно, что Петя нашел в 2 раза больше грибов, чем Юра. Значит, Юра нашел в 2 раза меньше грибов, чем Петя. Так как Петя нашел 20 грибов, а Юра в 2 раза меньше, то Юра нашел: 20 : 2 = 10, то есть 10 грибов».

Задание № 17 (с. 72).

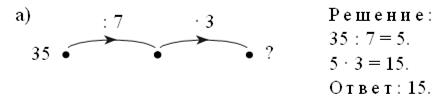
Учащиеся составляют схемы-«машины» и решают.

Запись:

Задача № 18 (с. 72).

– Прочитайте задачу.

– Что известно? Что требуется узнать?

– Составьте схему-«машину» или краткую запись и решите задачу.

Запись:

Решение:

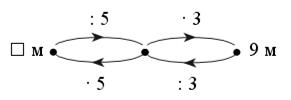
1) Сколько метров составляют пятую часть?

9 : 3 = 3 (м).

2) Сколько метров ткани было?

3 · 5 = 15 (м).

Ответ: 15 м.

2. Работа в печатной тетради № 2.

Задание № 136.

Скорее всего, учащиеся выполнят следующий чертеж:

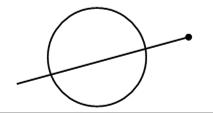(Две точки пересечения.)

Дополнительно учитель предлагает учащимся выяснить, сколько точек пересечения имеют окружность и луч на каждом чертеже:

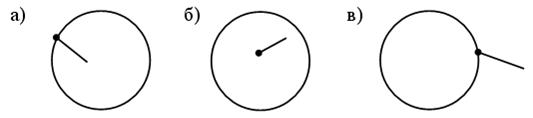
      (Две точки        (одна точка           (одна точка

     пересечения.)      пересечения.) пересечения.)

VI. Итог урока.

– Что нового узнали на уроке?

– Назовите признаки окружности.

– Назовите признаки луча.

Домашнее задание: № 14 (учебник); № 135 (рабочая тетрадь).

Урок 105