Работа по учебнику.
Задание № 1 (с. 64).
– Рассмотрите и сравните записи арифметических действий.
Учитель обращает внимание учащихся на то, что, хотя числа, над которыми производятся действия, во всех примерах одинаковы, в каждом из действий они называются по-разному. При этом при сложении и умножении данные числа называются словами, созвучными с названиями действий. Так, при сложении числа называются слагаемыми, а при умножении – множителями.
Названия чисел при вычитании и при делении запомнить труднее. Учащиеся могут пользоваться данной таблицей на первых уроках.
Задание № 2 (с. 64).
– Прочитайте данные примеры.
– Какое действие выполняется в каждом из примеров?
– Прочитайте примеры, используя слова «разность чисел», «сумма чисел», «произведения чисел» и «частное чисел».
Задание № 4 (с. 65).
Учащиеся выполняют записи:
54 : 9 = 6 8 · 7 = 56
97 + 3 = 100 50 – 30 = 20
Задание № 5 (с. 65).
Учащиеся записывают примеры, используя арифметические знаки, и проверяют, верно ли выполнены действия.
45 + 38 = 73 – неверно, так как 45 + 38 = 83.
6 · 7 = 42 – верно.
40 : 8 = 6 – неверно, так как 40 : 8 = 5.
60 – 11 = 59 – неверно, так как 60 – 11 = 49.
V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 12 (с. 66).
– Что значит выражение «увеличь в 8 раз»?
– Какое действие надо выполнить, если сказано «уменьши на 5»?
Далее учащиеся записывают примеры и находят их значение.
Запись:
(3 + 5) · 8 = 8 · 8 = 64.
(7 + 5) – 5 = 12 – 5 = 7.
(46 – 16) : 6 = 30 : 6 = 5.
Задание № 14 (с. 66).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– Запишите кратко условие задачи.
Запись:
Решение:
1) Чему равна длина манжеты?
56 : 7 = 8 (см).
2) На сколько сантиметров длина рукава больше длины манжета?
56 – 8 = 48 (см).
Ответ: на 48 см больше.
2. Работа в печатной тетради № 2.
Учитель обращает внимание учащихся на правильный выбор терминов.
Задание № 91.
Учащиеся работают самостоятельно и проверку выполняют самостоятельно, соотнеся свою работу с таблицей учебника (с. 68).
3. Работа по карточкам.
Карточка А
Подставь в «окошечко» числа 7, 9, 11, 15, 30.
Вычисли значения суммы.
Образец: 8 + 7 = 15.
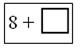7 9 11 15 30
Карточка В
Подставь в «окошечко» числа 6, 8, 14, 15, 20. Вычисли значения разности.
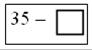6 8 14 15 20
VI. Итог урока.
– Что нового узнали на уроке?
– Как называются компоненты сложения? Вычитания? Умножения? Деления?
Домашнее задание: № 3, 13 (I столбик, учебник), № 128 (рабочая тетрадь).
Урок 100
названия чисел
в записях действий
Цели: учить употреблять названия компонентов сложения, вычитания, умножения и деления при чтении выражений; совершенствовать навыки решения задач с величинами «цена», «количество», «стоимость»; повторить правила построения и чтения математических графов, развивать внимание и мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Задача.
Ира собрала на 12 грибов больше Миши, но 7 её грибов оказались несъедобными. У кого и на сколько больше съедобных грибов?
2. Вычислите неизвестное число:
15 + = 20 + 7 = 30
60 – = 15 – 6 = 13
20 : = 5 · 7 = 42
9 · = 36 : 9 = 7
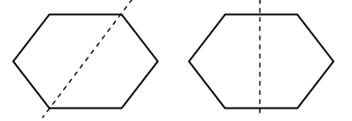
3. Постройте еще 1 такую же фигуру.
– Как она называется? (Шестиугольник.)
– Назовите признаки шестиугольника.
– Проведите в каждом из них по одному отрезку так, чтобы первый шестиугольник был разделен на 2 четырехугольника, а второй – на 2 пятиугольника.
4. Составьте «круговые» примеры:
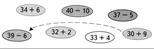
III. Сообщение темы урока.
IV. Работа по теме урока.
Задание № 6 (с. 65).
Учащиеся читают задание и выполняют записи:
4 + 27 = 31 6 · 8 = 48
12 – 5 = 7 72 : 9 = 8
Задание № 7 (с. 65).
Это задание направлено на развитие логического мышления учащихся. Выполняя задание, дети приводят доказательство утверждений.
1. Сумма двух чисел может быть равной первому слагаемому, если первое слагаемое – любое число, но при этом второе слагаемое – 0. Учащиеся могут привести следующие примеры:
0 + 0 = 0, 1 + 0 = 1, 17 + 0 = 17 И т. д.
2. Разность чисел может быть равной уменьшаемому, если уменьшаемое – любое число, а вычитаемое – 0. Учащиеся могут привести следующие примеры:
0 – 0 = 0, 32 – 0 = 32, 100 – 0 = 100 И т. д.
3. Разность чисел может быть равной вычитаемому, если уменьшаемое в 2 раза больше вычитаемого. Учащиеся могут привести следующие примеры:
6 – 3 = 3, 18 – 9 = 9, 4 – 2 = 2 И т. д.
Задание № 8 (с. 65).
Произведение двух чисел может быть равно первому множителю, если первый множитель – 0, а второй множитель – любое число или первый множитель – любое число, а второй множитель – 1.
Учащиеся могут привести следующие примеры:
0 · 0 = 0 0 · 9 = 0 5 · 1 = 5
0 · 1 = 0 1 · 1 = 1 12 · 1 = 12 И т. д.
Задание № 9 (с. 65).
Частное чисел может быть равным делимому, если делимое является любым числом, а делитель – 1 или делимое – 0, а делитель – любое число, кроме 0.
Учащиеся могут привести следующие примеры:
1 : 1 = 1 10 : 1 = 10 0 : 3 = 0
7 : 1 = 7 0 : 1 = 0 0 : 11 = 0 И т. д.
Дата: 2018-12-28, просмотров: 437.
