Для характеристики асимметрии и формы кривой распределения случайной величины служат коэффициент асимметрии и эксцесс.

Коэффициент асимметрии при нормальном распределении равен 0. Он рассчитывается по следующим формулам:

A = L₃⁰/S³,

L₃⁰ = (1/n-1)*[∑(x_i-χ)³].

Для обозначения L₃⁰ была использована та же формула, что и для расчета дисперсии, только отклонение от выборочного среднего возводится не в квадрат, а в третью степень.  В этом случае, если наше распределение не будет симметричным, то и коэффициент асимметрии A не будет равен 0, то есть мы будем иметь или положительную или отрицательную асимметрию, как показано на рисунке.

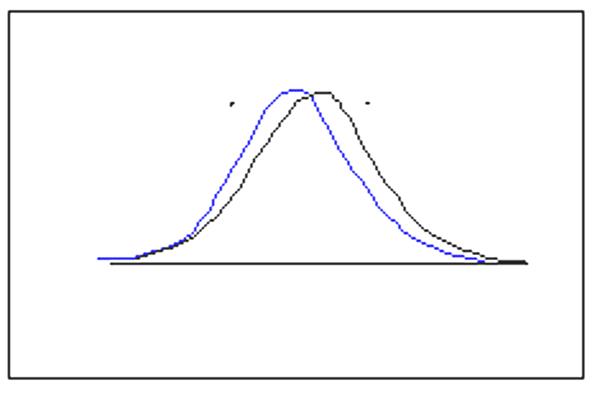
Рис . Асимметричные распределения.

Если мы хотим оценить форму кривой распределения, насколько наша вершина кривой распределения острая или сглаженная, то пользуются понятием эксцесса, который рассчитывают по формуле:

Э = L₄⁰/S⁴ - 3,

L₄⁰ = (1/n-1)*[∑(x_i-χ)⁴].

Эксцесс нормального распределения равен 0, кривая с более острой вершиной будет иметь положительный эксцесс, а более пологая кривая будет иметь отрицательный эксцесс, как отражено на рисунке. Положительный эксцесс свидетельствует о ненормальном однообразии изучаемой совокупности, а отрицательный эксцесс свидетельствует напротив как раз о ненормальном разнообразии изучаемой совокупности. В обиходном понимании эксцесс еще рассматривается как всплеск, например ненормального поведения, или всплеск энергии, что отражается на характере кривой распределения. Во всяком случае, оценить нормальность изучаемых совокупностей можно уже при расчете эксцесса и коэффициента асимметрии.

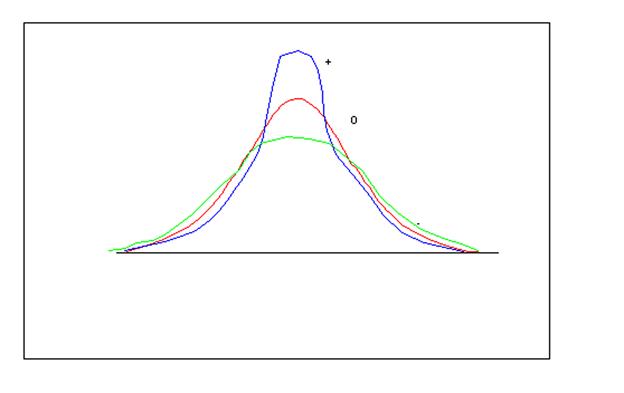
Рис. Положительный и отрицательный эксцесс.

Для определения параметров и статистик мы практически использовали одну и ту же формулу, в которой изменялся номер порядковой степени у суммы отклонений значений от арифметического среднего. Здесь мы сталкиваемся с понятием момента. Моментами  k-го порядка называют среднюю величину из  k-степеней отклонений вариантов x от некоторой постоянной величины C.

L_k = (x_i – C)

Это понятие широко используется в механике, в виде моментов инерции, различают начальные, условные и центральные моменты. Начальным моментом называют момент в котором С = 0, условным моментом называют, когда C равно произвольной величине и момент называют центральным, когда С = χ. В качестве характеристик случайной величины и используют первый начальный момент, когда

L₁ = x_i – 0;

второй центральный момент, когда

L₂ = ∑(x_i – χ)².

Соответственно, как было показано выше третий и четвертый центральные моменты были использованы для определения коэффициента асимметрии и эксцесса.