Измерений
При любых измерениях важно оценить их точность. Термин «точ-
ность измерения», т.е. степень приближения результатов к некото-
рому истинному значению, не имеет строгого определения и исполь-
зуется для качественного сравнения измерительных операций. Для
количественной оценки существует понятие «погрешность измере-
ния». Любой результат измерения является случайным, поэтому для
оценки его достоверности используются две характеристики: мате-
матическое ожидание М(0) = х — среднее значение, вокруг кото-
рого группируются все случайные результаты измерения х,...х„, и
дисперсия D(Ɵ) — степень разбросанности результатов относитель-
ного математического ожидания.
Понятия «точность» и «погрешность» можно пояснить на при-
мере стрельбы по мишени из артиллерийского орудия. Центр мише-
ни (точка наводки орудия на цель) — истинное значение, или мате-
матическое ожидание, причем M(Q) = 0. Точки попадания снарядов
в мишень — это результаты измерения (случайные величины), так
как на полет снаряда действуют случайные факторы: ветер, неравно-
мерно распределенная масса и сама масса снарядов, водные прегра-
ды (притягивают снаряды при их полете) и т.д. Точность стрельбы h
тем выше, чем кучнее, т.е. ближе к цели (центру мишени) ложатся
снаряды. Отклонение же снарядов от центра мишени характеризует-
ся погрешностью стрельбы δ; чем ближе к цели попадают снаряды,
тем меньше погрешность стрельбы и выше точность. Следовательно,
точность h и погрешность δ обратно пропорциональны: h- 1/|δ|.
Погрешность измерения (∆) — это отклонение результата изме-
рения от истинного значения измеряемой величины. Функциональ-
ная зависимость выходной величины имеет вид х = ƒ( х ; δ), где
∆ = х-х — погрешность результата.
Точность измерения ( h ) — это близость результатов измерения к
истинному значению измеряемой вели чины.
В общем виде погрешность измерения имеет следующие состав-
ляющие:
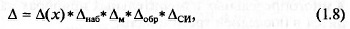
где ∆(х) — погрешность от нестабильности измеряемой величины х;
∆наб — погрешность наблюдателя; ∆м — погрешность метода измере-
ния; ∆обр — погрешность метода обработки результата; ∆сИ — погреш-
ность применяемого средства измерения.
Символом «*» обозначены знаки неопределенности суммирования
между составляющими погрешности измерения, так как вопрос о
законах сложения решается в каждом конкретном случае.
Таким образом, понятия погрешность измерения и погрешность
СИ отличаются друг от друга. Первые четыре составляющие погреш-
ности измерения могут быть уменьшены или даже сведены к нулю.
Последняя погрешность ∆си — погрешность СИ — является неустра-
нимой погрешностью.
Погрешности средств измерения ∆си классифицируются по ряду
признаков.
По форме з а п и с и погрешности СИ делятся на абсолютную ∆,
относительную δ и приведенную γ. Абсолютная погрешность — это
разность между результатом и истинным значением измеряемой ве-
личины:
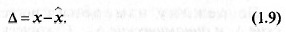
Эта погрешность характеризует только количественную сторону
результата измерения, но не отражает качественную сторону про-
цесса измерения; например, погрешность измерения расстояния
между двумя объектами ∆ = 2 км не позволяет однозначно сделать
вывод о качестве измерения. Относительная погрешность — это
отношение абсолютной погрешности к истинному значению из-
меряемой величины. Она характеризует погрешность результата
измерения
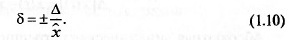
Измерительный прибор измеряет ФВ переменного значения. Его
качество не может характеризоваться относительной погрешностью,
так как она уменьшается с увеличением истинного значения изме-
ряемой величины:
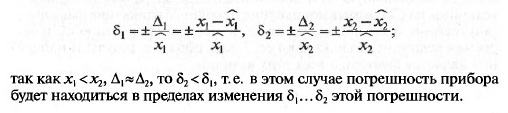
Любое же СИ должно характеризоваться одной погрешностью.
Исходя из этого существует «золотое правило» в метрологии:
в многопредельных измерительных приборах измерение ФВ прово-
дится в последней трети шкалы.
Качество измерительного прибора характеризуется приведенной
погрешностью. Приведенная погрешность — это отношение абсо-
лютной погрешности к базовому значению:
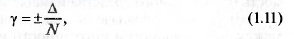
где N = const — базовое значение, за которое в измерительных при-
борах принят диапазон измерения N = (х в -х н ).
На практике вместо истинного значения измеряемой величины
используется ее действительное значение:
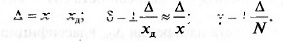
Относительная и приведенная погрешности могут выражаться не
только в безразмерных единицах, но и в процентах:
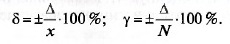
По режиму и з м е р е н и я погрешности делятся на статиче-
ские ∆ s , и динамические ∆ dy . Статическая погрешность формируется
в статическом режиме. Абсолютная погрешность СИ в статическом
режиме
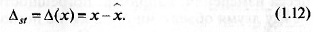
В динамическом режиме формируется динамическая погрешность.
Абсолютная погрешность СИ в динамическом режиме
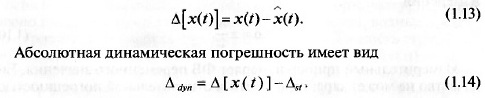
По в н е ш н и м у с л о в и я м п р и м е н е н и я СИ погрешности
делятся на основную ∆0 и дополнительную ∆с. Кроме измеряемой
величины на СИ оказывают влияние различные влияющие факторы φ,
(внутренние и внешние), которые не несут информацию об изме-
ряемой величине, но искажают ее. Таким образом, результат измере-
ния является функцией всех этих величин:
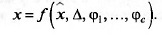
Для каждого СИ в нормативно-технической документации (НТД)
указываются диапазоны изменения влияющих факторов, которые для
данного СИ являются нормами (φ ref ). Эти значения могут быть даны
в виде одного числа (влажность W ref = 60%) или в виде диапазона
чисел (Ɵге/ = (20 ± 5) °С, U ref = 220 ±j° В )• Если в условиях эксплуатации
СИ влияющие факторы имеют нормальные значения или находятся
в пределах нормальной области этих значений (φ, = φге/), то такие
условия эксплуатации называются нормальными, а погрешность СИ,
формируемая в этих условиях, — основной, так как присуща только
самому СИ, отражает свойство только самого СИ и является его
основной (главной) погрешностью. Результат, полученный в нормаль-
ных условиях эксплуатации, равен

и формируется по каждому влияющему фактору φi.
Суммарная дополнительная погрешность ∆с равна
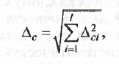
где ∆ci — дополнительная погрешность по φ, влияющему фактору;
l — число влияющих факторов.
В НТД на СИ кроме нормальных указываются также рабочие об-
ласти влияющих величин φi и дополнительные погрешности по
каждой из них, что позволяет определить общую погрешность для
конкретных условий измерения (если они не выходят за пределы
рабочих условий эксплуатации).
По х а р а к т е р у п о я в л е н и я погрешности СИ делятся на
систематическую ∆s и случайную ∆. Систематической называют
составляющую погрешности, остающуюся постоянной или изменяю-
щуюся по определенному закону от измерения к измерению. Обыч-
но систематические погрешности исключаются из результата изме-
рения различными способами. Случайной называют составляющую
погрешности, которая изменяется случайным образом при повторных
измерениях одного и того же истинного значения измеряемой вели-
чины. Исключить ее из результата невозможно, но оценить необхо-
димо. Для этого используются теория вероятностей и математическая
статистика.
По з а в и с и м о с т и между в е л и ч и н о й п о г р е ш н о с ти
и з н а ч е н и е м и з м е р я е м о й в е л и ч и н ы погрешности СИ
делятся на аддитивные, мультипликативные и гистерезиса.
Аддитивная погрешность постоянна по величине и не зависит от
значения измеряемой величины: ∆а(хi) = +а. Ее причиной, напри-
мер, может быть сбитая шкала СИ.
Мультипликативная погрешность пропорциональна измеряемой
величине: ∆ м (хi) = ± bx; ее причиной может быть, например, изме-
нение параметров отдельных элементов.
Погрешность гистерезиса — это несовпадение результатов из-
мерений при прямом и обратном ходе (причинами гистерезиса явля-
ются люфт, сухое трение, упругое последействие и т. п.). Количествен-
но погрешность гистерезиса (вариация) определяется как разность
между результатами измерений одного и того же значения измеряемой
величины, полученными при движении со стороны меньших значе-
ний до данного значения (прямой ход) и со стороны больших значе-
ний до данного значения (обратный ход). Вариация Н для стрелочных
приборов определяется по формуле Н = |х'-х"|,
где х' и х" — результаты, полученные соответственно при прямом и
обратном ходе.
При технических измерениях каждому СИ присваивается опреде-
ленный класс точности. Класс точности (А) — это обобщенная
метрологическая характеристика, определяющая различные свойства
СИ и включающая в себя систематическую и случайную составляю-
щий погрешности. Класс точности нормируется предельными значе-
ниями основной погрешности в виде абсолютной, относительной или
приведенной.
Классами точности, определенными по абсолютной погрешности
∆ ор , нормируются меры. Такой класс точности обозначается римской
цифрой или прописной буквой латинского алфавита, причем чем
больше цифра или дальше буква от начала алфавита, тем больше по-
грешность.
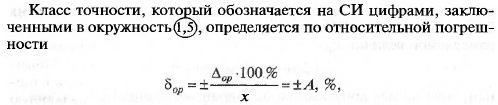
где х — результат измерения. Такими классами точности нормируют-
ся мосты переменного тока, счетчики электрической энергии, дели-
тели напряжения, измерительные трансформаторы. Цифровые СИ
нормируются классами точности, которые также определяются от-
носительной погрешностью
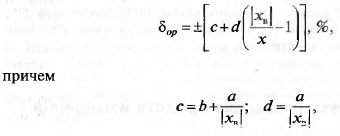
где а = ∆а(х) и b = ∆м(х) — аддитивная и мультипликативная состав-
ляющие погрешности соответственно; хi — верхний предел измерения
СИ. Такой класс точности может быть обозначен, например, 0,02 /0,01
(с = 0,02, d = 0,01). При нормировании класса точности по приве-
денной погрешности γор для СИ с неравномерной шкалой (например,
омметров и амперметров) она определяется по формуле

где x N — длина шкалы или ее части; обозначается такой класс точ-
ности на СИ цифрами с галочкой внизу — 1^5.
Для нормирования класса точности всех аналоговых СИ исполь-
зуется приведенная погрешность
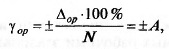
где N= х в -х и — предел измерения СИ.
Обозначается такой класс точности цифрами, например: 2,0. От-
влеченные положительные числа А, с, d в формулах выбираются из
ряда (1,0; 1,5; 2,0; 2,5; 4,0; 5,0; 6,0)10", где п = -3; -2; -1; 0; 1, и назы-
ваются классами точности.
Средство измерений может иметь два и более классов точности.
Например, при наличии у него двух и более диапазонов измерений
одной и той же физической величины (многопредельные измеритель-
ные приборы) или при измерении одним СИ нескольких физических
величин (разные классы точности для каждой измеряемой величины).
Зная класс точности СИ, можно определить действительное значение
измеряемой величин хд:
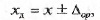
или, зная предел допускаемой основной погрешности ∆ ор , соответ-
ствует ли данное СИ своему классу точности.
Показателями качества измерения являются также правильность,
сходимость и воспроизводимость измерений. Правильность отража-
ет близость к нулю систематических погрешностей в их результатах.
Сходимость отражает близость друг к другу результатов измерений,
выполняемых в одинаковых условиях. Воспроизводимость отражает
близость друг к другу результатов измерений, выполняемых в раз-
личных условиях (в разное время, в различных местах, разными
методами и средствами измерения).
Дата: 2018-12-28, просмотров: 762.