Измерений

Метрологическая характеристика (MX) средства измерения —

это характеристика одного из свойств СИ, влияющая на результат

измерений и на его погрешность. Для каждого типа СИ устанавли-

ваются свои MX. Метрологические характеристики, устанавливаемые

в нормативно-технической документации (НТД) на данное СИ, на-

зываются нормируемыми MX, а определяемые экспериментально —

действительными MX.

К метрологическим характеристикам относятся статические и

динамические характеристики, чувствительность, порог чувствитель-

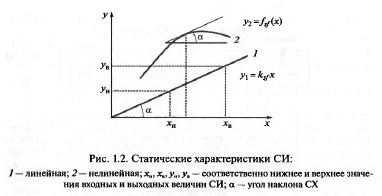
ности, диапазон измерения, цена деления шкалы и т. д. Статическая

характеристика (СХ) — это функциональная зависимость выходной

величины у от входной х в статическом режиме (рис. 1.2). При этом

режиме входные и выходные величины СИ не изменяются во време-

ни (стационарный или равновесный режим). Более точно СХ можно

определить как зависимость информативного параметра выходного

сигнала от информативного параметра входного сигнала в статиче-

ском режиме. В общем случае эта зависимость представляет собой

некоторое нелинейное уравнение преобразования у = f(x). Для из-

мерительных преобразователей и измерительных приборов с неиме-

нованной шкалой или со шкалой, отградуированной в единицах,

отличных от единиц измеряемой величины, СХ называется также

функцией преобразования, а для остальных измерительных прибо-

ров — характеристикой шкалы.

В реальных условиях эксплуатации на СИ действуют влияющие

факторы ср (внутренние и внешние), которые не несут информацию

об измеряемом параметре. Если они не равны нормам, то зависимость

у = f(x) называется рабочей СХ, а если равны — номинальной или

градуировочной СХ у = f у (x). Градуировочные характеристики СИ

получаются экспериментальным путем и могут быть заданы в виде

формул, графика или таблицы (например, градуировочные таблицы

для термометров сопротивления и термопар).

Важным параметром СИ является угол наклона статической ха-

рактеристики к оси абсцисс (для линейных СХ) или касательной к

этой характеристике в точке отсчета (для нелинейных СХ). Тангенс

угла наклона называется чувствительностью СИ (5). Чувствитель-

ность СИ — это свойство, определяемое отношением изменения

выходного сигнала этого средства к вызывающему его изменению

измеряемой величины:

Различают абсолютную и относительную чувствительности.

Абсолютная чувствительность определяется по формуле

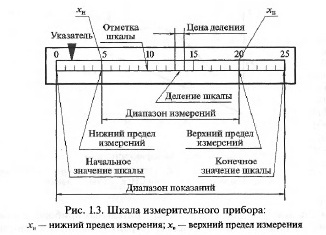
а относительная — по формуле

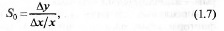
где ∆у — изменение сигнала на выходе СИ; ∆х — изменение изме-

ряемой величины; х — измеряемая величина.

Если статическая характеристика СИ нелинейна, то чувствитель-

ность в различных точках диапазона будет различной, а шкала — не-

равномерной. При линейной статической характеристике чувстви-

тельность СИ постоянна, а шкала равномерная.

Порог чувствительности СИ — это наименьшее значение из-

менения ФВ, начиная с которого может осуществляться ее измерение

данным средством.

Для шкальных отсчетных устройств используются характеристики,

показанные на рис. 1.3.

Цена деления шкалы (постоянная прибора) — разность значений

величины, соответствующих двум соседним отметкам шкалы СИ, т. е.

количество единиц величины, содержащихся в одном делении шкалы.

Диапазон измерений — область значений величины, в пределах ко-

торой нормированы допускаемые пределы погрешности СИ. Значе-

ния величины, ограничивающие диапазон измерений снизу и сверху

(слева и справа), называют соответственно нижним х_н и верхним х в

пределом измерений. Область значений шкалы, ограниченная на-

чальным и конечным значениями шкалы, называется диапазоном

показаний.

Цена деления шкалы С однозначно связана с числом делений п

шкалы и чувствительностью S:

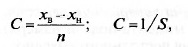
а число делений п — с классом точности (А) СИ: п > 10/2А (понятие

класса точности будет дано в подразд. 1.6).

Поэтому значение измеряемой величины должно быть отсчитано

по шкале с погрешностью в половину деления.

Динамическая характеристика СИ (рис. 1.4) — это зависимость

выходного сигнала от входного в динамическом режиме (в этом

режиме входные и выходные величины изменяются во времени)

y(t) = ƒ[х[( t ) ] ]. Динамический (неустановившийся, или переходный)

режим — переход СИ из одного установившегося режима в другой.

Так как практически все СИ имеют в своем составе инерционные

элементы (подвижные механические узлы; электрические, пневмати-

ческие или гидравлические емкости, индуктивности; элементы, об-

ладающие тепловой инерцией, и т.д.), то при мгновенном изменении

входного сигнала выходной сигнал изменяется с запаздыванием по

определенному закону (кривые переходных процессов, или кривые

разгона). Закон изменения этих характеристик может быть колебатель-

ным, апериодическим, дифференциальным, интегральным. Динами-

ческие характеристики описываются дифференциальными уравне-

ниями, передаточной функцией, амплитудно-фазовой, амплитудно-

частотной и фазо-частотной характеристиками (см. гл. 13), а также

переходной и импульсной функциями. Для определения параметров

динамических характеристик СИ используют теорию автоматическо-

го управления (регулирования). Важным параметром динамического

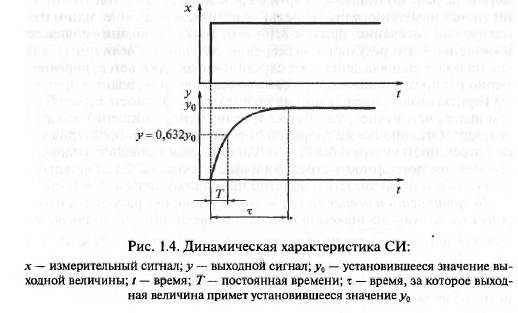
режима является время завершения переходного процесса (проме-

жуток времени т от момента подачи измерительного сигнала х до

момента установления постоянного выходного сигнала у = const). На

практике широко используется постоянная времени Т(это время, за

которое выходной сигнал достиг бы нового установившегося значе-

ния, если бы изменялся с постоянной скоростью, равной начальному

значению). Обычно за Т принимают время, за которое выходная

величина у достигает уровня у = 0,632у0, где у 0 — установившееся

значение выходной величины.