Любые измерения являются объектом метрологии — науки об

измерениях, методах и средствах обеспечения их единства и способах

достижения требуемой точности. Слово «метрология» образовано от

двух греческих слов:

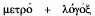
измерение, мера + учение, слово.

По своей сути метрология является наукой о получении количе-

ственной информации опытным путем, т.е. экспериментально, по-

средством измерения. Большинство реальных объектов обладает

таким многообразием свойств, что получить количественную инфор-

мацию о каждом из них невозможно, да и не нужно. С помощью

средств измерения (СИ) получают количественную информацию о

наиболее существенных свойствах объекта. Для сопоставления ре-

зультатов измерений, выполненных различными СИ в разных местах

и в разное время, необходимо обеспечить единство измерений.

Измерительная информация позволяет сформировать модель

объекта — упрощенное представление об объекте на основе коли-

чественных данных о его наиболее существенных свойствах. Чем

большее число свойств учитывается, тем точнее количественная ин-

формация о них, тем полнее модель отражает реальный объект. Ка-

чественное представление о модели объекта (номенклатура свойств,

представляющих интерес) должно быть сформировано заранее

(apriori), а измерительные задачи состоят в получении конкретных

количественных данных. Любое свойство может проявляться в боль-

шей или меньшей степени, т. е. иметь количественную характеристи-

ку. Следовательно, любое свойство может быть измерено. При этом

каждое свойство может быть охарактеризовано по-разному. Напри-

мер, пространственную протяженность можно характеризовать рас-

стоянием между двумя точками пространства, а можно углом между

направлениями на них из точки наблюдения.

Для проведения измерений необходимы измерительные шкалы.

В соответствии с МИ 2365-96 в теории измерений различают пять

основных типов шкал измерений: наименований, порядка, разностей

(интервалов), отношений и абсолютные.

Шкала наименований основана на приписывании объекту знаков

(цифр), играющих роль простых имен с целью их идентификации

или для нумерации классов (например, обозначения резисторов в

схеме — R6, RIS). По этому обозначению можно установить, что эле-

менты принадлежат к одному классу — классу резисторов. Но по этой

шкале нельзя установить, на сколько или во сколько их значения

больше (меньше) относительно друг друга, т.е. нельзя производить

операции сравнения и арифметические действия.

Шкала порядка (рангов) представляет собой ранжированный

ряд — упорядоченную последовательность размеров Q1<Q2< …<

<Qj <..., каждый из которых больше предыдущего, хотя сами раз-

меры неизвестны. Для обеспечения измерений по шкале порядка

некоторые точки на ней можно зафиксировать в качестве опорных

(реперных). Этим точкам шкалы могут быть присвоены цифры, на-

зываемые баллами. Знания, например, оцениваются по 4-балльной

реперной шкале: неудовлетворительно, удовлетворительно, хорошо,

отлично. Примерами таких шкал порядка являются: шкала Моаса для

определения твердости минералов (10 опорных точек), шкала Рихте-

ра для определения интенсивности землетрясений (12-балльная

шкала), шкала твердости металлов (Бринелля, Виккерса, Роквелла).

Недостатком шкал порядка является неопределенность интервалов

между реперными точками.

В шкале интервалов известен только масштаб между реперными

точками, сами же реперные точки (начало отсчета) выбираются про-

извольно по соглашению между учеными. По этой шкале можно судить

не только о том, что один размер больше другого, но и о том, на сколь-

ко больше. Однако по шкале интервалов нельзя оценить, во сколько

раз один размер больше (меньше) другого. К данным шкалам отно-

сятся шкалы температур (Фаренгейта, Реомюра, Цельсия).

Наиболее совершенной является шкала отношений. По ней мож-

но определить не только, на сколько один размер больше (меньше)

другого, но и во сколько раз он больше (меньше). Шкала отношений

представляет собой интервальную шкалу с естественным (абсолют-

ным) началом отсчета. Примером шкалы отношений является термо-

динамическая температурная шкала Кельвина (псевдоним англий-

ского ученого Джона Томпсона). В качестве естественной реперной

точки в этой шкале принят абсолютный ноль — при данной темпе-

ратуре прекращается тепловое движение молекул. По шкале Кельви-

на можно отсчитывать абсолютное значение температур и определять

не только на сколько градусов одна температура больше (меньше)

другой, но и во сколько раз больше (меньше):

Т\/Т 2 = п.

На современном этапе научно-технического прогресса измеритель-

ная информация нужна практически во всех областях человеческой

деятельности. Правильные, точные и достоверные измерения обеспе-

чивают соответствие выпускаемой продукции требованиям стандартов,

техническим условиям и другой нормативно-технической документа-

ции. Таким образом, измерения лежат в самой основе производства и

в огромной мере определяют возможность получения качественной

продукции. Массовость измерений, огромно'е разнообразие измеряемых

физических величин, методов и средств измерений, применяемых в

народном хозяйстве, потребовали разработки в рамках государственной

системы стандартизации единой системы метрологического обеспече-

ния разработки, производства, испытаний и эксплуатации продукции,

научных исследований и других видов деятельности во всех отраслях

хозяйства. Под метрологическим обеспечением понимается установ-

ление и применение научных и организационных основ, технических

средств, правил и норм, необходимых для достижения единства и тре-

буемой точности измерений. Общие единые правила и нормы метро-

логического обеспечения устанавливаются в стандартах Государствен-

ной системы обеспечения единства измерений (ГСИ).