Инженерно-техническое сооружение трубопроводного транспорта имеет иерархическую структуру, состоящую из головных сооружений, линейной части, площадных объектов, участков перехода через препятствия. В свою очередь каждый элемент структуры делится на строительные объекты и технологическое оборудование.
Рассчитать себестоимость сооружения трубопроводного транспорта можно только по его структуре. Структуру сооружения представляем в виде ориентированного графа, строим все пути графа и по каждому пути вычисляем себестоимость строительно-монтажных работ и расход материалов в денежном выражении, соответствующие варианту размещения магистрального нефтепровода.
Исходными данными являются варианты размещения площадных объектов, себестоимость строительно-монтажных работ по возведению площадных объектов, себестоимость строительно-монтажных работ по сооружению линей части нефтепровода и таблица совместимости объектов различных классов.
В результате расчетов определяются оптимальный вариант размещения площадных объектов и оптимальный вариант структуры магистрального нефтепровода, обеспечивающий наименьшую сумму себестоимости строительно-монтажных работ и расхода материалов в денежном выражении.
Существуют специальные средства автоматизации проектирования линейной части магистральных нефтепроводов. Однако они не позволяют рассчитать и оптимизировать себестоимость сооружения трубопроводного транспорта.
Для решения задач расчета и оптимизации себестоимости строительно-монтажных работ по возведению линейной части магистрального нефтепровода применяются геоинформационные системы.
Основными экономическими задачами проектирования линейной части магистрального нефтепровода являются:
- составление сметы затрат на строительно-монтажные и проектно-изыскательные работы (СМ и ПИР), выполняемые на территории,
- калькуляция плановой себестоимости 100-метрового отрезка линейной части магистрального нефтепровода,
- технико-экономическое обоснование вариантов проекта строительства линейной части магистрального нефтепровода,
- оптимизация себестоимости СМ и ПИР, выполняемых в процессе строительства.
Значение технико-экономических показателей, указанных выше, и методы их расчета зависят от инженерно-геологических условий местности, где проходит дорога, поскольку расценки одних и тех же СМ и ПИР зависят от данных условий. Поэтому для решения указанных задач целесообразно использовать геоинформационные системы.
Для составления сметы затрат на СМ и ПИР, выполняемых на территории, применяются программы создания, редактирования и сканирования электронных карт и видеобазы. В данном случае электронные карты являются геологическими картами (разрезами) с привязкой к прямоугольной системе координат на плане местности, где проходит дорога, нефтепровод, магистраль.
Для технико-экономического обоснования вариантов проекта нефтепровода участок территории на электронной карте разбивают на части с однородными инженерно-геологическими условиями и определяют себестоимость 100-метрового отрезка нефтепровода, которая не зависит от направления этого отрезка.
Согласно техническим условиям проектирования, границу раздела аппроксимируют ломаной линией, состоящей из 30 прямолинейных участков, на каждом участке выбирают точку, определяющую направление нефтепровода, вычисляют себестоимости СМ и ПИР по 30 вариантам и находят самый дешевый вариант.
Данные операции можно автоматизировать и, кроме того, можно аналитически определить направление нефтепровода с наименьшей себестоимостью СМ и ПИР.
Опишем алгоритм решения задачи оптимизации себестоимости СМ и ПИР, выполняемых в строительстве магистрального нефтепровода. Он основан на выборе оптимального направления нефтепровода при переходе границ участков с разными инженерно-геологическими условиями. Оптимальными считаются направления нефтепровода, которые обеспечивают наименьшую себестоимость строительства с учетом инженерно-геологических условий местности.
Выберем i-ый отрезок границы раздела. Его уравнение в прямоугольной системе координат электронной карты:
y=kix+ci, ai 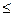 x
x 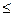 bi
bi
ai, bi, ci, ki легко найти в системе «Электронная карта». Выберем на i-ом отрезке произвольную точку M(x, kix+ci) и вычислим себестоимость СМ и ПИР на участке железнодорожной магистрали АМ, ВМ, соединяющем начальную точку А с точкой М с конечной точкой В. Данная величина зависит от x и равна
S(x)=(c1L1+c2L2)/100,
где c1- себестоимость 100-метрового отрезка нефтепровода на первом участке местности,
где c2- себестоимость 100-метрового отрезка нефтепровода на втором участке местности,
L1- расстояние (в метрах) от точки A до точки M,
L2 - расстояние (в метрах) от точки B до точки M.
Пусть координаты точек А, В в прямоугольной системе координат электронной карты A(a1, a2), B(b1, b2). Тогда
L1= 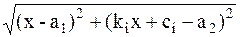
L2= 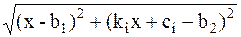
S(x)=c1 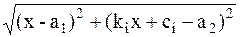 +c2
+c2 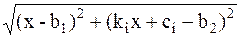
Легко доказать, что экстремальные точки S(x) являются корнями уравнения 4-й степени и могут быть найдены аналитически.
Вычисляя экстремальные точки и сравнивая значения S(x) в этих точках со значениями S(ai), S(bi), находим на каждом отрезке границы оптимальное направление нефтепроводной магистрали. Сравнивая себестоимости СМ и ПИР по этим оптимальным направлениям, находим наилучшее направление нефтепровода, обеспечивающее наименьшую себестоимость СМ и ПИР.
Для определения оптимального варианта размещения площадных объектов магистрального трубопровода нужно разработать параллельные алгоритмы и программы построения графа структуры и программы расчета каждого пути графа.
Вначале упорядочиваем комплекс сооружений. К первому классу относятся площадные объекты, ко второму классу относятся компрессорные станции, к третьему классу относятся насосные станции и т.д. Совместимые объекты k- ого и k+1- ого класса соединены участком трубопровода.
Вершины графа- номера элементов групп. Дуги графа соединяют вершины, соответствующие совместимым элементам соседних групп. Начало дуги- вершина с меньшим номером, конец дуги- вершина с большим номером.
Путем, соединяющим вершину k- ой группы Vk с вершиной n- ой группы Vn, (n>k), называется последовательность попарно совместимых вершин (Vk, Vk+1, Vk+2….Vn) из групп k, k+1, k+2,…..n. Длина пути определяется как сумма себестоимостей строительно-монтажных работ на объектах Vk, Vk+1, Vk+2….Vn, вычисляемых для каждого объекта Vi по расчетной таблице, и себестоимостей линейной части. Направление каждого участка линейной части выбирается так, чтобы себестоимость строительно-монтажных работ на выбранной направлении была оптимальной. Процесс выбора оптимального направлений линейной части трубопровода описан выше.
Задача оптимизации себестоимости строительства магистральных нефтепроводов сводится к построению всех путей, соединяющих вершины первой и последней группы и определению среди них пути наименьшей длины. Решение данной задачи получено на базе вычислительных сетей, мультипроцессорных вычислительных комплексов и распределенных кластеров.
Решение оптимизационной задачи удовлетворяет принципу оптимальности Беллмана и может быть получено методом последовательного улучшения. Согласно тому методу, производится последовательный пересчет кратчайших путей, соединяющих вершины первой и k-ой группы, в кратчайшие пути, соединяющие вершины первой и k+1-ой группы. После пересчета в качестве текущего массива кандидатов для решения оптимизационной задачи записывают массив кратчайших путей, соединяющих вершины первой и k+1-ой группы. Дойдя до последней группы, получают всех кандидатов для решения оптимизационной задачи и выбирают и них наилучшего.
На каждом шаге процесса записываем все кратчайшие пути, соединяющие фиксированную вершину первой группы и переменные вершины k-ой группы. Значения кратчайших путей- это значения массива b, элементы которого- символьные строки, где перечислены через запятую вершины пути. Выбираем вершину k+1-ой группы и дополняем кратчайшие пути, соединяя выбранную вершину и вершины k-ой группы при условии, что выбранная вершина совместима с вершиной k-ой группы.
Вычисляем длины полученных путей и находим наименьшее значение длин полученных путей. Определяем путь с наименьшей длиной и записываем его вершины. Получаем кратчайший путь, соединяющий вершину первой группы и выбранную вершину k+1- ой группы. В конце выводим значения кратчайших путей, соединяющих вершины первой и последней группы, в ячейки электронной таблицы.
Для расчета кратчайших путей используются программа вычисления путей, соединяющих вершины первой и второй групп, и программа пересчета кратчайших путей.
В программе вычисления путей, соединяющих вершины первой и второй групп, используются следующие массивы и переменные:
l(i,i1)- длина пути, начинающегося в вершине i первой группы и заканчивающегося в вершине i1 второй группы,
b(i,i1)- путь, начинающийся в вершине i первой группы и заканчивающийся в вершине i1 k- ой группы,
ng- нижняя граница номеров объектов второй группы,
a- количество объектов первой группы,
n- количество объектов второй группы,
Текст программы вычисления путей, соединяющих вершины первой и второй групп
a=Worksheets(«Справочник»).cells(1,2)
n=Worksheets(«Справочник»).cells(2,2)
ng=a
for i=1 to a
for i1=1 to n
if Worksheets(«Нормативы»).cells(i,ng+1+i1)>0 then
r(i,i1)=Worksheets(«Справочник»).cells(i,3)*Worksheets(«Нормативы»).
cells(i,ng+i1+1)
l(i,i1)=Worksheets(«Справочник»).cells(i,3)*Worksheets(«Справочник»). cells(i,2) +расход* Worksheets(«Справочник»).cells(ng+i1,2)
b(i,i1)=str(i)+”,”+str(ng+i1) else
b(i,i1)= «Нет» : end if : next i1 : next i
В программе пересчета кратчайших путей используются следующие массивы и переменные:
l(i,i1)- длина кратчайшего пути, начинающегося в вершине i первой группы и заканчивающегося в вершине i1 k- ой группы,
l1(i,i2)- длина кратчайшего пути, начинающегося в вершине i первой группы и заканчивающегося в вершине i2 k+1- ой группы,
b(i,i1)- кратчайший путь, начинающийся в вершине i первой группы и заканчивающийся в вершине i1 k- ой группы,
b1(i,i2)- кратчайший путь, начинающийся в вершине i первой группы и заканчивающийся в вершине i2 k+1- ой группы,
ng- нижняя граница номеров объектов k- ой группы,
ng1- нижняя граница номеров объектов k+1- ой группы,
a- количество объектов первой группы,
n- количество объектов k- ой группы,
n1- количество объектов k+1- ой группы,
m- количество групп объектов.
В программе по значению элементов массивов r(i,i1), l(i,i1), b(i,i1) определяются значения элементов массивов r1(i,i2), l1(i,i2), b1(i,i2).
Текст программы пересчета кратчайших путей
a=Worksheets(«Справочник»).cells(1,2)
for k=2 to m-1
n=Worksheets(«Справочник»).cells(k,2)
n1=Worksheets(«Справочник»).cells(k+1,2)
ng1=ng+n
for i=1 to a
for i2=1 to n1
min=10000000
for i1=1 to n
if b(i, i1)<>«Нет»and Worksheets(«Нормативы»).cells(ng+i1,ng1+1+i2-a)>0 then
расход= r(i,i1)* Worksheets(«Нормативы»).cells(ng+i1,ng1+1+i2-a)
длина= l(i,i1)+расход* Worksheets(«Справочник»).cells(ng1+i2,2)
if длина < min then
min= длина
d=расход
номер=i1
end if : end if : next i1
if min=1000000 then
b1(i,i2)= «Нет» else
r1(i,i2)=d
l1(i,i2)=min
b1(i,i2)= b(i,номер)+ “,”+ str(ng1+i2)
end if : next i2
ng=ng1
for i2=1 to n1
r(i,i2)= r1(i,i2)
l(i,i2)= l1(i,i2)
b(i,i2)= b1(i,i2) : next i2 : next k
c=Worksheets(«Справочник»).cells(m,2)
for i=1 to a
for j=1 to c
Worksheets(«Ответ»).cells( i,j)= b(i,j) : next i : next j
ЛИТЕРАТУРА
а) основная литература:
1. Черноруцкий И. Методы оптимизации. Компьютерные технологии [Электронный ресурс].- СПб. : БХВ-Петербург, 2011.-384 с.- Электронное издание. - Гриф УМО.- ISBN 978-5-9775-0784-4
2. Аттетков, А.В. Введение в методы оптимизации [Электронный ресурс].- Электронное издание.- М.: Финансы и статистика, 2011.- 272 с
б) дополнительная литература:
3. Т.В.Ростовцева, В.И. Фомин, С.Е.Пономарев. Применение алгоритмов теории графов для оптимизации в строительстве и производстве. Санкт-Петербург, 2012, Ó СПбГИЭУ, 2012.
4. С.Е.Пономарев. Теория графов и параллельные вычисления в нефтегазовом комплексе, 2014, Ó LAMBERT Akademic publishing.
Дата: 2018-12-28, просмотров: 347.