Изучаем тему на примере решения задач 1, 2.
Задача 1
Прутки длиной 8 метров разрезаются на заготовки длиной 3 и 2.4 м, Заготовок первого типа нужно получить не менее 25 штук, а второго - не менее 36 штук. Определить минимальное число разрезаемых прутков. Допускаются лишь способы разрезки, при которых длина остатка меньше любой заготовки.
РЕШЕНИЕ
Детали можно разрезать тремя способами. В первом варианте получается только две заготовки длиной 3 м., во втором варианте получаются одна заготовка длиной 3 м. и две заготовки длиной 2,4 м., в третьем варианте получаются три заготовки длиной 2,4 м.
Вводим целочисленные переменные xi, (i=1, 2, 3). x1- количество прутков, разрезанных первым способом, x2 - количество прутков, разрезанных вторым способом, x3- количество прутков, разрезанных третьим способом. Целевая функция x1+x2+x3 должна быть минимальной. Ограничения следуют из условия, что заготовок первого типа должно быть не менее 25 штук а заготовок второго типа - не менее 36 штук.
Для решения задачи можно составить таблицу:
| Длина прутка | 8 | ||
| Заготовка 1 | 3 | ||
| Заготовка 2 | 2.4 | ||
| Заготовка 1 | Заготовка 2 | Количество прутков | |
| Способ 1 | 2 | 0 | x1 |
| Способ 2 | 1 | 2 | x2 |
| Способ 3 | 0 | 3 | x3 |
| Количество заготовок | 2*x1+x2+0*x3 | 0*x1+2*x2+3*x3 |
Ограничения: 2*x1+x2+0*x3≥25; 0*x1+2*x2+3*x3≥36; x1≥0; x2≥0; x3≥0; x1, x2, x3 – целые.
Целевая функция: x1+x2+x3.
Записываем ограничения и целевую функцию в электронную таблицу и с помощью поиска решений получаем ответ.
Задача 2
Заданы поставщики и потребители. Нужно построить оптимальный план поставки, при котором первый поставщик обеспечивает максимально возможное число потребителей.
 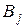
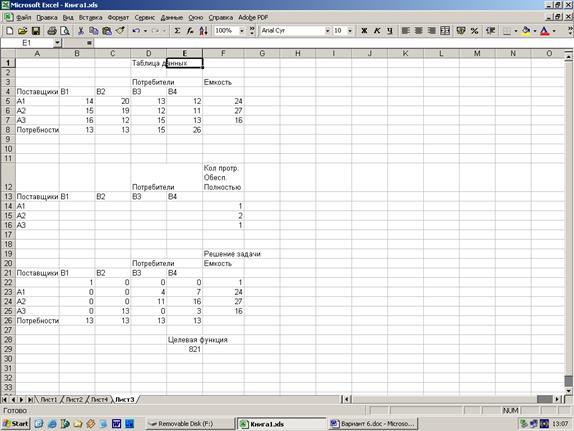
| 11 | 10 | 17 | 29 |
| 27 | 14 | 20 | 13 | 12 |
| 27 | 15 | 19 | 12 | 11 |
| 16 | 16 | 12 | 15 | 13 |
РЕШЕНИЕ
Вначале определяем наибольшее количество потребителей, которых первый поставщик может обеспечить полностью. Для этого сортируем потребности pi по возрастанию и находим такое число n, что сумма р1+p2+….+pn меньше или равна емкости первого склада а сумма р1+p2+….+pn +pn+1 больше емкости первого склада. Найденное значение равно наибольшему количеству потребителей, обеспеченных полностью первым поставщиком. Для автоматизации данного процесса нужно составить программу на VBA
Вводим в таблицу данных исходные данные
В таблицу Решение задачи вводим неизвестные, ограничения и целевую функцию. В ячейках B22:E22 записываем значения переменных x1i, равных 1, если 1-ый поставщик обеспечивает полностью i-ого потребителя, и 0 в противном случае. В остальных ячейках таблицы решения задачи записываем вывоз груза. Сумма x1i равна числу потребителей, которых полностью обеспечил первый поставщик.
Вводим следующие ограничения:
=СУММ(B23:E23)+СУММПРОИЗВ(B22:E22;B8:E8)
=СУММ(B24:E24)
=СУММ(B25:E25)
=B8*B22+СУММ(B23:B25)
=C8*C22+СУММ(C23:C25)
=C8*C22+СУММ(C23:C25)
=C8*C22+СУММ(C23:C25)
Целевая функция:
=СУММПРОИЗВ(B5:E7;B23:E25)+СУММПРОИЗВ(B5:E5;B22:E22;B8:E8)
Запускаем Поиск решения, устанавливаем знаки ограничений и получаем ответ.
Тема 7. Сетевые методы в планировании и управлении
Задача о последовательной обработке.
Разработка системы нормативно-справочного обеспечения задач оптимизации производства
В связи с изменением технологии производства изменяются состав и нормы выработки технологических операций, состав, количество и производительность исполнителей при выполнении технологических операций. Состав выполняемых работ и количество исполнителей изменяется также при проведении планово-предупредительного и капитального ремонта. Поэтому актуальной задачей АСУ является обеспечение процессов оптимизации производства нормативно-справочной информацией.
Нет смысла копировать вручную данные из тарификационных справочников в таблицу поиска решений. Работа эта трудоемкая, и к моменту ее окончания данные становятся неактуальными.
Для решения задач нормативно-справочного обеспечения оптимизации производства нужна информационная система, заполняющая таблицу поиска решений данными, выбираемыми пользователем в тарификационном справочнике.
Процесс разработки данной системы изучаем на примере задачи об оптимальном распределении исполнителей по независимым работам. Рассмотрим ситуацию, когда на производственном участке выполняются n технологических операций и для их выполнения используются k исполнителей, имеющих разные производительности при выполнении конкретной технологической операции. Нужно распределить исполнителей по технологическим операциям так, чтобы к концу смены достичь максимального объема выпуска продукции в натуральном выражении. То есть, для конкретного исполнителя следует определить время выполнения той или иной технологической операции таким образом, чтобы к концу смены на производственном участке объем выпуска готовой продукции был наибольшим.
Сформулируем поставленную задачу как задачу оптимального программирования. Введем переменные xij- время выполнения i-ой операции j-ым исполнителем, (1 ≤ i ≤n, 1 ≤ j ≤k). Переменные xij удовлетворяют следующим ограничениям:
0 ≤ xij; 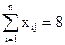 , (1 ≤ j ≤k) (1)
, (1 ≤ j ≤k) (1)
Обозначим pij производительность исполнителя j при выполнении технологической операции i, Vi- объем выполнения работы i. Объем выполнения работы i Vi равен
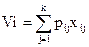 , (1 ≤ i ≤n)
, (1 ≤ i ≤n)
Между объемами выполнения технологических операций существуют линейные зависимости:
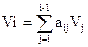 , (2 ≤ i ≤n) (2)
, (2 ≤ i ≤n) (2)
Из (2) следует, что объемы Vi , (2 ≤ i ≤n), Выражаются через V1. Таким образом, нужно найти наибольшее значение 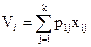 , изменяя значения переменных xij, удовлетворяющих ограничениям (1), (2).
, изменяя значения переменных xij, удовлетворяющих ограничениям (1), (2).
Задачу представляют в табличной форме. В расчетной таблице задают диапазон ячеек для записи значений переменных, формулу целевой функции и формулы ограничений. Для получения оптимальных значений переменных xij используется поиск решений, настроенный по формату таблицы оптимизационной задачи.
Для решения задачи используются справочник работ, тарификационный справочник и таблица связей между объемами выполнения технологических операций. Из справочника работ в автоматическом режиме в расчетную таблицу записываются наименования работ, выбираемых пользователем. Из тарификационного справочника в автоматическом режиме в расчетную таблицу записываются наименования исполнителей, выбираемых пользователем, из таблицы связей между объемами выполнения технологических операций в автоматическом режиме в расчетную таблицу записываются коэффициенты, выбираемые из строк, соответствующих работам, выполняемым на участке.
Для решения оптимизационной задачи нужно разработать информационные объекты, технологию работы пользователя и программное обеспечение.
Информационные объекты - это справочник работ, тарификационный справочник, таблица связей между объемами выполнения технологических операций и расчетная таблица. В справочнике работ заданы коды работ, наименования, единицы измерения и нормы выработки в единицу времени. В справочнике исполнителей заданы наименования рабочих профессий, разряды и производительность исполнителей при выполнении различных технологических операций. В таблице связей между объемами выполнения технологических операций заданы коэффициенты линейных зависимостей.
В справочнике работ пользователь отмечает работы, выполняемые за смену, в тарификационном справочнике пользователь указывает количество конкретных исполнителей, работающих по графику. Эти данные записываются в расчетную таблицу.
Программа заполнения расчетной таблицы состоит из трех процедур:
1. Процедура заполнения списка выбранных работ
2. Процедура заполнения списка выбранных профессий
3. Процедура вычисления производительности исполнителей выбранных работ
Первые две процедуры – стандартные программы работы со справочной информацией. Третья программа вычисляет с помощью стандартной операции поиска образца в документе номера строк, соответствующих выбранным пользователем наименованиям работ, номера граф, соответствующих выбранным пользователем наименованиям исполнителей, и записывает их в массивы. По найденным массивам определяются ячейки расчетной таблицы, в которые записываются данные, необходимые для решения оптимизационной задачи. Ниже приводятся тексты процедур.
Процедура заполнения списка выбранных работ
n=3: k=5
while worksheets(«Справочник»).cells(n,2)<>””
worksheets(«Оптимизация»).cells(k,1)= worksheets(«Справочник»).cells(n,1)
k=k+1: n=n+1: wend
Процедура заполнения списка выбранных профессий
n=3: k=5
while worksheets(«Справочник»).cells(n,5)<>””
worksheets(«Оптимизация»).cells(3,k)= worksheets(«Справочник»).cells(n,4)
worksheets(«Оптимизация»).cells(4,k)= worksheets(«Справочник»).cells(n,5)
k=k+1: n=n+1: wend
Процедура вычисления производительности исполнителей выбранных работ
n=3:dim a(100) as integer: dim b(100) as integer
while worksheets(«Оптимизация»).cells(n,1)<>””
c= worksheets(«Оптимизация»).cells(n,1)
k=2: while worksheets(«Справочник»).cells(k,1)<>c and Worksheets(«Справочник»).cells(k,1)<>””
k=k+1: wend: a(n)=k
n=n+1: wend
n=5
while worksheets(«Оптимизация»).cells(3,n)<>””
c= worksheets(«Оптимизация»).cells(3,n)
k=2: while worksheets(«Справочник»).cells(k,4)<>c and Worksheets(«Справочник»).cells(k,4)<>””
k=k+1: wend: b(n)=k
n=n+1: wend
n=3
while worksheets(«Оптимизация»).cells(n,1)<>””
r=a(n)
k=5: while worksheets(«Оптимизация»).cells(3,k)<>””
e=b(k)
worksheets(«Оптимизация»).cells(n,k)= worksheets(«Оптимизация»).cells(4,k)* Worksheets(«Справочник»).cells(r,e)
n=n+1: wend
Дата: 2018-12-28, просмотров: 338.